Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

I. ОКТЕТНАЯ ЭЛЕКТРОДИНАМИКА

Термы теории имеют вид: ∂/u∂t + i∂/∂dx + j∂/∂y + k∂/∂z + αEĤ + βI∂/∂dp_x + βJ∂/∂dp_y + βK∂/∂dp_z, φ + iA_x + jA_y + kA_z + Eψ + IB_x + JB_y + KB_z, где φ - скалярный электрический потенциал, А - векторный магнитный потенциал, y - скалярный магнитный потенциал, B - векторный электрический потенциал, α = μ/m_иu³, β = μm_и, μ = m´/m, u - характерная скорость взаимодействий, m_и - мера инерции, m´ - константа октетной физики, определяющая темп генерации материи, m - мера количества материи. Система уравнений октетной электродинамики:

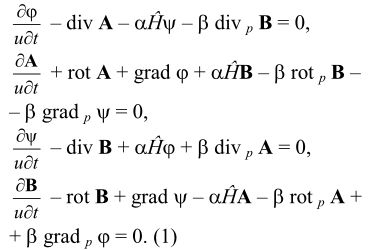
Пусть ψ = 0, В = 0, тогда для электродинамики получаем кватернионный вариант:

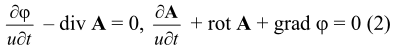
и дополнительные условия для потенциалов:

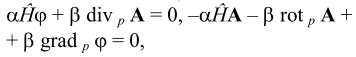
или в развернутом виде:

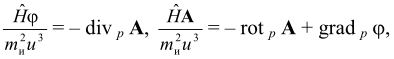
откуда при u → ∞ следуют уравнения: div _p A = 0, rot _p A = grad _p φ.

Обратим внимание на следующий результат. В пространстве кватернионов K (с = 1) составим операторный и предметный термы:

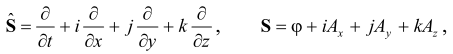
откуда после их перемножения получим:

 (f)

(g)

Полагая , из (g) образуем систему:

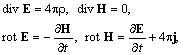(h)

где ,

.

Переопределением плотностей заряда и тока можно привести эту теорию к уравнениям Даламбера. Пусть , где , и , где . Тогда получается система уравнений:

(h´)

Следовательно, произведенные замены показывают, что волновые уравнения и, соответственно, волновые процессы возможны и имеют место только относительно абсолютно неподвижной в любой движущейся системе отсчета S эфирной субстанции Ω. Это следует из независимости плотностей ρ₀ и  от фактора времени, то есть вытекает из их стационарности и фиксированности вариаций ,  ,  относительно эфирных вкладов , .

Неизменность  и  приводит к калибровочной инвариантности потенциалов φ и А, но индифферентна к конкретному значению скорости распространения электромагнитных возмущений проявленной среды. Последнее означает, что скорость распространения является свойством именно среды, ее электромагнитной плотности, а не «плотности» эфира. Образно говоря, фотон движется не в эфире, а всегда в эфире покоится, как и любой «ощущаемый» физический объект. Возможны новые эффекты, зависящие от поляризации токов и зарядов по отношению к эфиру. В гиперкомплексных пространствах размерности n > 4 гиперкомплексные смещения плотностей заряда и тока многограннее, и их физический смысл связан, возможно, с новыми степенями свободы, что также может привести к обнаружению практически значимых явлений.

Если μ = 0, то из (1) получим систему (3):

 - div A = 0,  + rot A + grad φ = 0,  - div В = 0, - rot В + grad ψ = 0.

Там, где А = В, нет вихревого магнитного поля H = rot A, а уравнения приобретают вид: +  - 2div A = 0, 2 + grad φ + grad ψ = 0.

Обозначив F = rot B, G = -  - grad ψ для напряженностей дуальных электрического и магнитного полей, соответственно, получим систему уравнений:

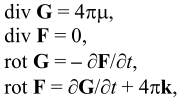
где 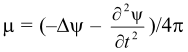- плотность магнитного заряда,

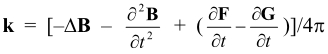 - плотность магнитного тока.

Система (1) устанавливает взаимосвязь плотностей токов и зарядов j, k, r, m, но это другая теория. Однако токи и заряды могут быть переопределены согласно экспериментальной юстировке (в микро- и мегамире).

II. МЕХАНИКА И ЭЛЕКТРОДИНАМИКА

Система уравнений биоктетной механики преобразуется в систему:

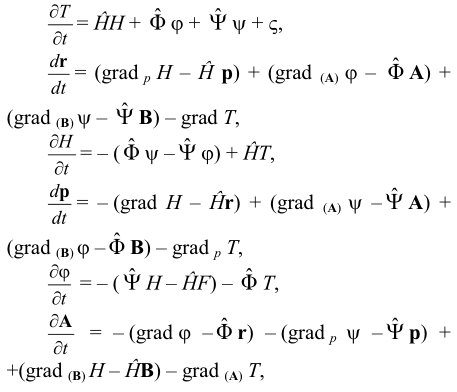
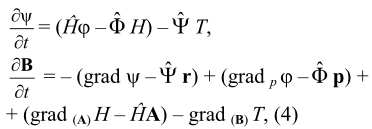
коэффициенты в которой определены ранее ([1 - 2], см. список лит. Части 6), но с соответствующими изменениями для электромагнитных величин. Здесь ς - показатель необратимости провремени (зависящий от размерности физических величин, в т.ч. от количества координат пространства), φ - потенциал электрического поля, ψ - дуальный потенциал электрического поля, А - магнитный векторный потенциал, В - дуальный магнитный векторный потенциал, , - операторы, аналогичные операторам , , но связанные с электромагнитными явлениями. Операторы oper _(W) соответствуют величинам W. Ввиду дуальности (в гиперкомплексном смысле) биоктетной физики система (4) инвариантна относительно умножения на любую комбинацию гиперкомплексных единиц с постоянными коэффициентами, в том числе на произвольную j ∈ Q. Это позволяет не переопределять напряженности полей, при ψ = 0, В = 0 из калибровочных условий:

для H = rot A, E = - grad φ при u = 1 получая систему:

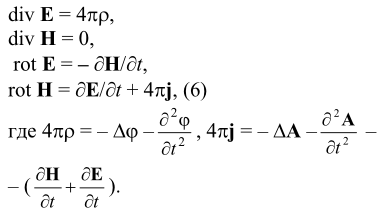
Но при этом нужно иметь в виду инвариантное преобразование. Другая альтернатива: можно переопределить напряженности полей, не останавливаясь на факте преобразования. Данное замечание фиксирует своеобразную взаимосвязь и релятивизм статусов времени и скалярного электрического потенциала. Дальнейшее расширение теории допускается при записи вместо j и других потенциалов во второй смежной октаве динамических компонент обобщенной механики - с трансляцией электромагнитных величин в следующие измерения пространства над Q.

Пример 3. Начальные условия: v = 0, w = 0, E ≠ 0, f = 0, m > m´ (объект покоится, перекачки не равной нулю энергии нет, механических сил нет, масса велика). Пусть, далее, φ ≠ 0, А = 0, ψ = 0, В = 0. Тогда при p = 0, H = mu² + φ, Ĥ = - h²Δ/2m + φ, где h - аналог постоянной Планка, в приближении о(1/u³) получим систему из 9 уравнений 16-физики:

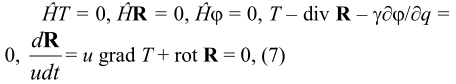
где γ - константа связи (1/137?), q - параметр, «обязанный» введению 5-й порождающей единицы Q. Зависимость φ = φ(q) и постоянная g задаются из внешней теории.

Если w ≠ 0, f ≠ 0, то при тех же условиях получаем систему:

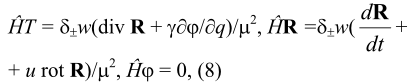
где δ_± - структурный коэффициент, μ = m/m´, Ĥ = - h²Δ/2m + wT + φ.

Пример 4. Начальные условия: v = 0, w ≠ 0, Н ≠ 0, E = 0, f ≠ 0, m > m´ (объект покоится, есть перекачка энергий, в сумме равных нулю, есть механические силы, масса велика). Пусть φ = 0, А ≠ 0, ψ = 0, В = 0. В приближении о(1/u³), p = 0, H = mu² + wT + A_z, Ĥ = -h²Δ/2m + wT + A_z получаем систему (9):

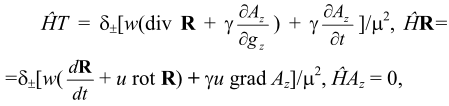
где параметр g_z, как и зависимость A_z = A_z(g_z), определяется из внешней теории и/или экспериментально.

Система (9) демонстрирует новый уровень квантованности, касающийся структурности материи: либо Т, и/или R, и/или А постоянны (и тогда wT = -A_z), либо эти физические величины ведут себя неклассически (фрактально). На основе систем уравнений (8 - 9) возможно создание аналитических моделей взаимодействия нескольких носителей необратимых термодинамических процессов, вводя нейропсихическое пространство. Аналитические модели Ходжкина - Хаксли [5], будучи пионерскими, относятся к другой феноменологии физической нейрокибернетики.

Z Замечание 1. Хотя все функции в системе уравнений могут быть представлены в форме волновой функции Ψ, - Ĥ = -h²Δ/2m + U + wT - аналог квантово-механического оператора действует на амплитуды вторично, после действия производящего физические величины из общей (обобщенной) Ψ универсального оператора : Ψ = 0 ⇒ U = 0, где в частности для компоненты Е ∈ Q может быть ĤH = 0.

Уравнение Ψ = 0 не рассматривается по причине того, что: 1) волновой характер физических состояний заложен в структуре пространства Q; 2) с помощью данного (априорного) оператора  уже произведена выборка физических величин - сообразно идее, заложенной в алгебрах Гейзенберга. Таким образом, оператор Ĥ является следом в физике Ф_D над Q, "оставшимся после коллапса" Ψ ввиду гамильтоновой конкретизации (алгебраического приведения) механики - написания канонических уравнений.

III. ПРИЛОЖЕНИЯ

3.1. АВТОСОЛИТОН МЕТАГАЛАКТИКИ

Правая часть системы (1) в [1] может содержать гармонические источники (аналогично для (5)), в частности при ∂Т/∂t и ∂Н/∂t. Теория будет большей размерности. Возможен вариант А_Т =А_Тocos(ωt), А_H = А_Hosin(ωt), когда рассматривается только неподвижный начальный центр генерации материи и провремени. Тогда импульсы и координаты тел будут являться следствиями креатистских процессов в очагах становления из эфира. В обоих случаях решения описывают эволюцию Метагалактики. В принципе, указанная система уравнений  является нелинейной, допускает гармонические решения для Т и Н - даже без гармонической правой части. Все три варианта дают следующую картину эволюции Метагалактики.

Пробное тело в Метагалактике движется согласно осцилляциям - свяжем их с неоднородностью распределения материи, влияющей на метрику пространства-времени. В начале отсчета, т.е. вблизи очага становления, осцилляции тела происходят с большими амплитудами. По мере удаления от центра местные амплитуды плавно падают, а периоды - возрастают. В фазовом пространстве - движение по медленно закручивающимся спиралям (с всплеском в «точке» накопления). Величины Н и Т испытывают сложные изменения. Подбором амплитуд внешних для данной теории воздействий можно привести решения к согласию с астрономическими данными.

При повышении информативности аппарата описания физической реальности на базе удвоения гиперкомплексных систем [4] для адиабатического расширения (или сжатия) Метагалактики обнаруживается зависимость:

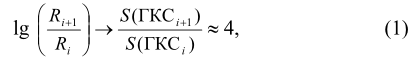
где R_j - характерный размер j-го космического образования, S(ГКС_j) - ему соответствующая энтропия, ГКС - гиперкомплексная система. Энтропия S(ГКС_j) ~ |ТБУj |   R, где |ТБУj | = (2 ^j)² - «размер» таблицы бинарного умножения. Отсюда видно, что накапливаемая при удалении от наблюдателя на периферию структурная энтропия S = 28 для Метагалактики.

Примечательно, что эти оценки детерминированного образования космических неоднородностей при расширении антропогенной вселенной находятся в согласии с формализмом построения из предкового множества Y потомственных множеств {X_i}:

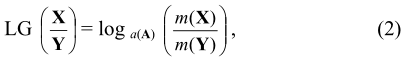
где LG - обобщенная функция (логарифмический функционал), а и m - меры на множестве А оснований и множестве W, соответственно. Если делитель в (2) - ядро гомоморфизмов J(Y → X), X = N - множество натуральных чисел, Y = P - множество простых чисел, то 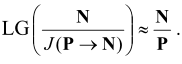Конкретно для распределения чисел получим: 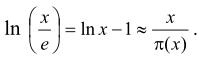Этот закон открыл еще П. Л. Чёбышев. Для ГКС над полем Р справедлива теорема: 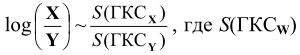- энтропия описания множества W с помощью ГКС, дробь справа - отношение количеств энтропии в формировании потомственного множества Х из предкового множества Y (при расширении пространства, при экспансии материальных структур, при генерации натуральных чисел и т.д.). Для смежных множеств получаем:

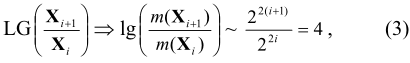
где при X_j = R_j, j = 0 можно принять: R_o = 1.

Наблюдаемые в астрономии неоднородности Метагалактики обладают гармонической периодичностью: 1) Метагалактика - lg R ~ 28; 2) расстояния между галактиками - lg R ~ 24; 3) ядра галактик - lg R ~ 20; 4) планетная система - lg R ~ 16; 5) типичная звезда - lg R ~ 12; 6) нейтронная звезда - lg R ~ 8; 7) планетарные неоднородности - lg R ~ 4; 8) основная мода реликтовой гравитационной субстанции - lg R ~ 0.

Вывод 1. После ее генерации из эфира экспансия материи наблюдается во всём, даже прослеживается в эволюции гносеологии (!?); в проблеме P ⇒ N теория чисел является ее отражением. Но за островной статистикой материи видна гармоническая закономерность - волнообразное рассеяние материи является автосолитоном Метагалактики.

3.2. ФЛОГИСТОН МАССЫ И ДАЛЬНОДЕЙСТВИЕ

Система уравнений (см. Часть 3), если Т = 0 и μ = 0, после определения «постоянной гравитации» γ из калибровочного 1-го уравнения Ф_D над О:

     (4)

где γ = 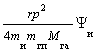, Ψ_и = ,

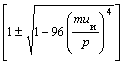при u → ∞ примет инерционную форму:

            (5)

откуда получаем:

В этом уравнении нет массы вообще, а движение есть. Конкретное решение в окрестности гиперсферы x_s*x_s ≈ R ² имеет вид:

, где в частности ω_s = , a_s = .

Анализ показывает, что между пробными телами расстояние возрастает, и они уходят на бесконечность независимо от начальных условий. Этот эффект моделирует постоянную генерацию материи «из ничего» с последующим рассеянием.

Для u → 0 при знаке « - » получим систему:

  (6)

при знаке « + » систему:

             (7)

решения которых качественно те же.

Если ψ= 0, то система имеет аналогичные решения.

3.3. ГЕОМЕТРИЧЕСКИЙ КРИСТАЛЛ

Рассмотренные уравнения допускают решения, согласно которым два тела уходят на бесконечность, испытывая нестандартное взаимодействие. В результате их траектории образуют сложную спираль, форма и топология проекции которой на фиксированную плоскость меняются в зависимости от характерной скорости u. Символично структурное совпадение Re (φ_s²) и Im (φ_s²), где φ_s = iω_s + a_s, с формулами из теории эфира (В. Зеллмейер, 1871): n² - k² = 1 + , 2nk = ,

где n - показатель преломления, k - коэффициент поглощения, константы a, b,  меняются от слагаемого к слагаемому и в разных теориях имеют различные значения. В калибровочных по «константе тяготения» теориях n - декремент, k - частота, взаимно меняющие свои функции в комбинациях знаков « + » и « - » (при ускоренном движении безмассовых частиц в пространстве октав и μ = 0, Т = 0, u → ∞).

Приведенные формулы объясняют дисперсию влиянием «резонирующих молекул, вкрапленных в эфир, на скорость распространения световой волны. Эта же идея была разработана с электромагнитной точки зрения...» (П.С. Кудрявцев. Курс истории физики. - 1982). Таким образом, при u → ∞ выявляется одна базовая структура пространства О, допускающая определенный класс взаимодействий и движений на различных уровнях организации материи - идентичного характера. Это и есть геометрический кристалл, обнаруживаемый при возвращении дальнодействия в основания физики.

Постулат пространства Q содержит этот вывод, но открытие гиперкомплексного исчисления произошло на фундаменте глубокого понимания Гамильтоном, Кэли и Диксоном закономерностей и тем самым устраняет неопозитивизм Ф_D.

3.4. ИНТЕРВАЛ И ПРОВРЕМЯ

Реальная часть интервала в Q имеет вид: Re(ds_*ds) = dt ² - dr ² - dH ² - dp ² - dφ ² - dψ ² - -dΞ ² - ..., где для краткости опущены коэффициенты размерности и связи. Чисто гиперкомплексная часть Im(ds_*ds) определяет динамическую фрактальную структуру, характеризуемую вращениями вокруг выделенных осей координат. Циклические компоненты получаются умножением ds = dt + idx + jdy + kdz + EdH + Idp_x + Jdp_y + Kdp_z +  dφ + dψ + ... на себя. Таким образом, обобщение интервала в [1] - в случаях: а) целочисленных размерностей физических величин; б) определения приращений времени - принимает вид:

dt´=dt , (8)

где v - относительная скорость тел, f - удельная сила (плотность силы), w - удельная мощность (плотность мощности), далее - удельные изменения со временем величин φ, ψ, Ξ... в системе измерений S, связанной с объектом 1; отсчет времени t´ связан с объектом 2. Из (8) видно, что в одной из «систем отсчета» нет сил, выделения (поглощения) энергии и иных характеристик состояния физического объекта.

Интервал (8) при наличии сил и других (нескомпенсированных, таких как, например, возрастание энтропии) изменений объектов (в объектах) возвращает времени статус абсолютной величины, не зависящей от способа синхронизации часов в инерциальных системах отсчета. Это устраняет многие парадоксы позитивистской физики, в частности - «парадокс близнецов» в СТО. С другой стороны, аналитически подтверждается правомерность опытов А.И. Вейника, обнаружившего зависимость темпа локального инструментального времени вблизи необратимых термодинамических процессов. Те же эффекты возможны под воздействием мощных биофизических процессов, например при нервно-психическом возбуждении. В последнем случае «деформации» численных значений физических величин не зависят от направления процесса. В пределах линейности элементарного интервала эффект будет один и тот же, в частности, при отрицательных и положительных эмоциях, измеренных в соответствующей системе единиц и одинаковых по модулю. Нелинейные системы записываются в форме:

ds = f_tdt + if_xdx + jf_ydy + kf_zdz + Ef_HdH + If_pxdp_x + Jf_pydp_y + Kf_pzdp_z,+ f_jdφ + ...

где f_q = f_q(t, x, y, z, H, p_x, p_y, p_z, φ...).

Пример 1. С точки зрения наблюдателя на Земле (система измерений S) у космонавта в полете (система измерений ) время течет иначе: dt = dt´ ,

где учитываются только три воздействия в (8), v = v(t) - относительная скорость наблюдателей, f = f(t) - сила торможения корабля в поле тяжести звезды или ядра Галактики, w = w(t) - мощность, потребляемая / выделяемая при его развороте (затрачиваемая на коррекцию орбиты).

С точки зрения путешественника в , фиксирующего свое состояние по приборам звездолета, движется с ускорением землянин, сам же он - фактически в невесомости (или, согласно ОТО, путь его лежит по геодезической). Поэтому

dt´  = dt ,

где f - кажущаяся сила, действующая на землянина, причем f ² = ², если массы наблюдателей одинаковы.

Сравнивая (а) и (b) без различения инертной и гравитационных масс, получаем: dt(S) ≠ dt( ) ввиду несимметричности процессов и их времени в системах S и  (не изменяет темпоральной картины устранение кажущейся силы). Аналогично для dt´.

Другой подход к вопросу преобразований состоит в рассмотрении приращения физических величин, а не обобщенных координат и принимаемого за время параметра t классической механики:

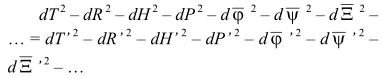
Соответственно рассматривается Im(dS*dS) - для компонент j ∈ Q, где j - единица (обобщенно) неассоциативного моноида Q. Здесь все величины являются или могут являться функциями параметрического времени t и обобщенных координат x_s, p_s, m_s..., где s = 1, 2, 3 для одночастичной системы (для n-частичной системы индексация меняется). В принципе, допускается зависимость T, R, H, P, φ... от других, внешних переменных, например подобная наложению связей в аналитической механике. Нелинейный вариант аналогичен (2).

Пример 2. Приращение провремени в случае рассмотрения обобщенных координат и постгамильтонова оператора Ĥ = -h²Δ/2m + U + wT записывается в виде:

dТ = d   ,    (9)

где  .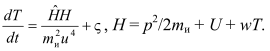

Провремя определяется из системы уравнений (1) октетной физики и (5) - биоктетной теории [1]. Постгамильтонов вариант H = р²/2m_и + U(r) + wT, Ĥ = -h²Δ/2m_и + U(r) + wT в О ведет к системе уравнений:

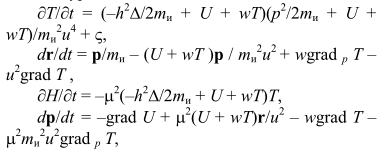
из уравнений 1 и 5 которой получаем уравнение для Т:

ΔТ = аТ ² + bT + c

где a = 2m_иw/h², b = 2m_и[αμ²/r + w²(p²/2m_и + 2α/r)/m_и²u⁴] / (μ² + w²/m_и²u⁴)h², c = 2αm_иw(p²/2m_и + 2α/r) / rm_и²u⁴h²(m² + w²/m_и²u⁴) при U = α/r с координатами x_s, p_s, определяемыми из остальных уравнений.

Очевидно, решения уравнения (е) должны удовлетворять условиям: Т(∞) = 0, Т(0) ≠ 0 и Т(0) ≠∞. Система (d) показывает, что Т индивидуально для частицы в центральном поле, для каждого взаимодействующего тела. Для системы тел в целом Т едино. Для Метагалактики ΔТ ≈ аТ ².