Колебания среды, возникающие в твердом теле при высоких температурах, оказывают значительное влияние на образование в нем структурных дефектов. Изучение характера распространения колебаний в упруго-пластической среде является актуальной задачей физики конденсированного состояния. Взаимосвязь колебаний плотности структурных дефектов и смещений среды можно описать с помощью калибровочной теории дефектов [1].
Целью работы является определение частот колебаний упруго-пластической среды с дефектами структуры.
Из полевых уравнений теории [1] следуют уравнения непрерывности и равновесия в обобщенной форме:
, (1)
где 
, 
, 
; греческие индексы принимают значения 0, 1, 2, 3, а латинские - 1, 2, 3; 
- коэффициенты упругой жесткости кристалла; ρ = const - плотность материала; c - скорость света; 
- тензор деформаций кристалла; αij - тензор теплового расширения кристалла, α0a=0; T - температура.
uαβ = (∂βuα + ∂αuβ + θαβ + θβα)/2, (2)
где 
- вектор смещений; θαβ - компоненты объектов аффинной связности, обусловленные трансляционными дефектам, например, краевыми дислокациями.
Основные уравнения имеют более простой вид в случае изотропной среды. Коэффициенты упругой жесткости вычисляются по формуле:
cijkl = λ∙δijδkl+μ∙δilδjk+ν∙δikδlj. (3)
Подставив (2) и (3) в (1), получим уравнение динамики среды с дефектами:
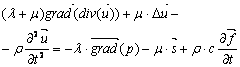, (4)
где 
, 
, 
, по повторяющимся индексам подразумевается суммирование. Правая часть уравнения (4) содержит вынуждающие силы.
Направим ось Ox по направлению распространения волны, тогда вектор смещений ui(x,t) можно разложить на продольную и поперечные составляющие вида A0exp{i(ω∙t+k∙x)}.
Величины p, si, fi зададим в виде гармонических колебаний с амплитудами A1, A2, A3 соответственно, сдвинутых по фазе на величину φ относительно смещений. Подставим ui(x,t), p(x,t), si(x,t) и fi(x,t) в (4). Для продольных колебаний получим уравнение:
-(λ+2μ)k2+ρω2 = (- i∙λkτ1 - μτ2 + iρcωτ3)eiφ, (5)
для поперечных колебаний:
- μk2+ρω2 = (- i∙λkτ1 - μτ2 + iρcωτ3)eiφ, (6)
где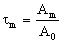 
, m = 1, 2, 3.
Решив уравнения (5), (6) относительно ω, получим два корня:
, n = 0,1, (7)
где для продольных колебаний:
,
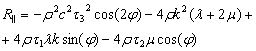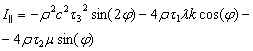
для поперечных колебаний:
,
.
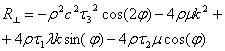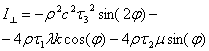Мнимая часть выражения (7) определяет коэффициент нарастания (затухания) колебаний. Волновые решения с Imwn ≠ 0 физически не реализуются в твердом теле.
Найдем частоты волн колебаний, распространяющихся в среде с дефектами. Положим мнимую часть ωn равной нулю и определим значение разности фаз φ. Для упрощения расчетов выберем τ2 = τ3 = 0, тогда получим два значения φ0 = π/2, φ1 = - π/2, при которых
для поперечных колебаний
ωn = ( |(-1)n k∙μ + τ1∙λ|∙k / ρ )1/2, n = 0,1; (8)
для продольных колебаний
ωn = ( |(-1)n k∙(λ+2μ) + τ1∙λ|∙k / ρ )1/2, n = 0,1 (9)
Частоты (8) и (9) соответствуют физически возможным решениям уравнения (4) для незатухающих волн деформации. При τ1 = 0 выражения (8), (9) переходят в известные выражения для волн в упругой среде без дефектов. Структурные дефекты влияют на частоту распространяющихся волн. Зависимость ωn от отношения амплитуд τ для продольных колебаний показана на рис. 1. Для частоты поперечных колебаний график имеет аналогичный вид. В расчетах использованы значения λ = -5,09∙1011 Н/м2 и μ= 5,31∙1011 Н/м2, ρ = 2,3 ∙ 103 кг/м3, k = 1 м-1.
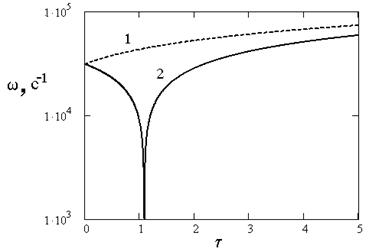
Рисунок 1. Зависимость частоты продольных волн в упруго-пластической среде от отношения амплитуд τ: 1 - ω0(τ); 2 - ω1(τ)
Функция ω0(τ) монотонно возрастает при τ>0. Функция ω1(τ) имеет минимум, в котором частота достигает значения ωmin = 0, что соответствует стоячим волнам. Длина стоячих волн зависит от значения τ.
Таким образом, получены следующие типы решений: 1 - непрерывно возрастающие (убывающие) по амплитуде волны, реально не наблюдаемые; 2 - незатухающие волны деформации, в дисперсионные соотношения которых входят упругие постоянные среды, плотность среды, отношение амплитуд колебаний вынуждающей силы и смещений.
СПИСОК ЛИТЕРАТУРЫ
[1] Bogatov N.M. Gauge field theory of dislocations formation by thermal stresses // Phys. Stat. Sol. (b). 2001. V. 228. №3 P.651- 661.