Оценка качества формулы приближенного интегрирования при функционально-аналитическом подходе предполагает использование критерия минимальности нормы функционала погрешности в соответствующем пространстве. Нормы функционалов определяются через экстремальные функции, которые являются обобщенными решениями некоторых дифференциальных уравнений в частных производных. Дифференциальный оператор такого уравнения порождается видом нормы функции в основном пространстве. Задачи этого круга восходят своими истоками к работам С.Л.Соболева 60-70 гг., где теория оценивания погрешности приближенного интегрирования была построена для гильбертовых пространств 
[1], [2]. Дальнейшее обобщение происходило одновременно в направлениях от к 
(
) В.И.Половинкиным [3] и от факторизации к 
Ц.Б.Шойнжуровым [4]. Теория для негильбертова показателя суммируемости разработана Ц.Б.Шойнжуровым [5], и независимо ряд сходных результатов получен М.Д.Рамазановым [6]. При разработке теории в вводились специальные способы нормирования пространства с помощью преобразования Фурье фундаментального решения известного дифференциального оператора. Разработка теории для пространств с естественными нормами, являющимися прямым обобщением норм из начата Ц.Б.Шойнжуровым [7] и продолжена нами [8]. В настоящее время исследования распространяются на функциональные пространства с нормами, осложненными весовыми функциями. Данная работа посвящена нахождению представлений линейных функционалов в весовом пространстве Соболева через суммируемые функции. Наличие представлений функционалов погрешности кубатурных формул в исследуемых пространствах позволяет получать оценки погрешности численного интегрирования для этих классов функций, в некоторых случаях неулучшаемые.
Предварительные сведения.
Пространство 
определяется как замыкание пространства S Шварца в норме
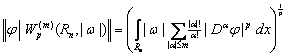,(1)
где 
- весовая функция произвольного знака, такая, что произведения 
суммируемы в p-й степени. Отметим, что в работах [1], [5] и других применялась весовая функция, неотрицательная на всей области определения.
Оператор 
, где Δ - оператор Лапласа, порождается нормой [5]
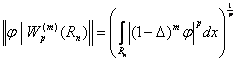, (2)
Оператор 
порождается нормой [8]
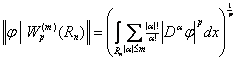, (3)
Результаты.
Теорема 1. Фундаментальные решения 
и 
операторов и принадлежат пространству 
, 
, , 
.
Доказательство основано на оценках производных 
, 
, приведенных в [9], и на свойствах множителя Марцинкевича, каковым является отношение образов Фурье этих операторов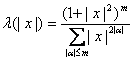 
. Благодаря последнему факту оценки производных оказываются справедливыми для 
, что дает для 
-норм
, .
Принадлежность всех производных фундаментального решения весовому пространству влечет утверждение теоремы.
Отметим, что условие определяет вложение рассматриваемого пространства в пространство непрерывных функций, и что при этом условии существуют интегралы, оценивающие производные фундаментальных решений в окрестности начала координат. Условие непрерывности обязательно в теории кубатурных формул, так как дельта-функции функционала кубатурной суммы действуют на непрерывные функции.
Следствие. Свертка фундаментального решения с функционалом 
принадлежит пространству . Такая свертка является решением линейного дифференциального уравнения в обобщенных функциях, в частности образованного каким-либо из рассматриваемых операторов, когда правая часть равна функционалу .
Теорема 2. Существует представление линейного функционала в весовом пространстве Соболева через фундаментальное решение
.
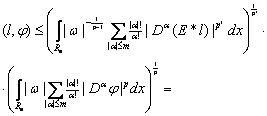
Доказательство проводится с применением неравенств Гельдера для сумм и интегралов, что приводит к оценке, основанной на утверждении следствия из теоремы 1
Замечание. В фактор-пространствах 
, где подобные представления содержат частные производные только высшего порядка, нормы и представления являются однородными, иными словами функционалы в этих пространствах представлены билинейными формами.
Теорема 3. Существует представление линейного функционала в весовом пространстве Соболева через экстремальную функцию 
Доказательство основано на приведении вариационной задачи к дифференциальному уравнению в обобщенных функциях, в котором экстремальная функция функционала удовлетворяет условию 
. Отправным положением является то, что в рефлексивном пространстве, каким является при максимум функционала, равный его норме, достигается на единичной сфере
.
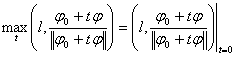Составленная функция является непрерывной по параметру t. С использованием необходимого условия экстремума и с учетом единичности нормы функции 
выводится искомое представление. Функции φ0 и ψ0 связаны равенством 
.
Правомерность дифференцирования под знаком интеграла установлена при помощи оценок, содержащих нормы функций. Единственность решения уравнения установлена при помощи неравенств для весовых пространств Соболева, обобщающих неравенства Кларксона.
СПИСОК ЛИТЕРАТУРЫ
- Соболев С.Л. Введение в теорию кубатурных формул. - М.: Наука, 1974.
- Соболев С.Л., Васкевич В.Л. Кубатурные формулы. - Новосибирск: Изд-во ИМ СО РАН, 1996.
- Половинкин В.И. Последовательности кубатурных формул и функционалов с пограничным слоем: Автореф. дис. ... докт. физ.-мат. наук. - Л., 1979.
- Шойнжуров Ц.Б. Оценка функционалов погрешности кубатурной формулы в пространствах с нормой, зависящей от младших производных: Дис. ... канд. физ.-мат. наук. - Новосибирск, 1967.
- Шойнжуров Ц.Б. Теория кубатурных формул в функциональных пространствах с нормой, зависящей от функции и ее производных: Автореф. дис. ... докт. физ.-мат. наук. - Улан-Удэ, 1981.
- Рамазанов М.Д. Лекции по теории приближенного интегрирования. - Уфа: Башгосуниверситет, 1973.
- Шойнжуров Ц.Б. Решение одного класса квазилинейных уравнений второго порядка эллиптического типа в неограниченной среде // Математический анализ и дифференциальные уравнения: Межвуз. сб. науч. тр. - Новосибирск, 1992. - С. 109-113.
- Корытов И.В. Оценка функционалов погрешности кубатурных формул в функциональных пространствах Соболева: Автореф. дис. ... канд. физ.-мат. наук. - Красноярск, 1997.
- Никольский С.М. Приближение функций многих переменных и теоремы вложения. - М.: Наука, 1977 .