Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Рассмотрим систему дифференциально-разностных уравнений следующего вида

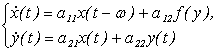
где ω>0 - положительное число, t≥t₀ и f(0) = 0.

Условия Рауза-Гурвица для системы (1) имеют вид:

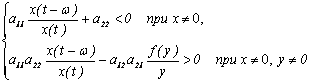
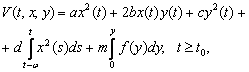(3)

где .

При выполнении условий: a>0, c>0, ac - b² > 0, d>0, m>0, f(y)y>0 при у ≠ 0 и для всех t≥t₀ функционал Ляпунова (3) является положительно определенным, т.е.

Справедливы следующие утверждения.

Теорема 1. Если выполняются условия

а) ,

б) ,

в)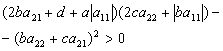

г)

д) ,

где , то тривиальное решение системы (1) устойчиво.

Доказательство. Для доказательства теоремы используем функционал Ляпунова

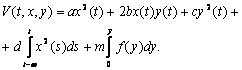
Тогда

При выполнении условий а) -д) это выражение не положительно и функция V(t,x,y) не возрастает. Это доказывает устойчивость тривиального решения системы (1).

Теорема 2. Если выполняются условия

а) ,

б) ,

в)

г) ,

где  и , то тривиальное решение системы (1) устойчиво.

Теорема 3. Если выполняются условия

а) ,

б) ,

в)

г)

д) ,

где  и , то тривиальное решение системы (1) устойчиво.

Теорема 4. Если выполняются условия

а) ,

б) ,

в)

г)

д) , где  и , то тривиальное решение системы (1) устойчиво.

Доказательства теорем 2-4 приводятся небольшой модификацией доказательства теоремы 1.

СПИСОК ЛИТЕРАТУРЫ

1. Е.А. Барбашин. Функции Ляпунова. М.: Наука, 1970.
2. Беллман Р. и Кук К.Л. Дифференциально-разностные уравнения. М.: Мир, 1967.