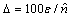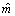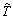Далее рассмотрим неоднородности распределений 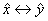 для случаев однофакторного моделирования. Полученные методические выводы можно экстраполировать на идентификацию многофакторных статистических моделей [1]. Традиционно модели строятся для изучения корреляционных связей между факторами. В реальных условиях, особенно в экологии и экономике, существуют так же некорреляционные связи, которые называются скедастическими.
для случаев однофакторного моделирования. Полученные методические выводы можно экстраполировать на идентификацию многофакторных статистических моделей [1]. Традиционно модели строятся для изучения корреляционных связей между факторами. В реальных условиях, особенно в экологии и экономике, существуют так же некорреляционные связи, которые называются скедастическими.
По этому поводу в работе [3, с.63] отмечается следующее: «Стохастическая связь имеет два частных случая - корреляционную и скедастическую связь. Если при изменении одной величины изменяются только средние значения другой (и наоборот), а дисперсия и тип закона распределения остаются неизменными, такая связь называется корреляционной ... . Если же меняется только дисперсия, а среднее арифметическое постоянно, то это скедастическая связь». Производственные и природохозяйственные связи являются корреляционно-скедастическими.
На рис. 1 приведены примеры графиков различных взаимосвязей y = f (x) . Эти графики вполне наглядны и не требуют дополнительных пояснений.

Рис. 1. Виды взаимосвязей величин [129]: а - функциональная; б - стохастическая корреляционно-скедастическая; в - корреляционная; г - скедастическая с убывающей дисперсией, переходящая в функциональную связь
Пусть какой-то процесс по воспроизводству леса устойчив и стабилен, то есть зона устойчивости по схеме на рис. 6в сходится в центр устойчивости, а параметры лесосырьевой базы и ресурсы лесной экосистемы соответствуют стационарному случайному процессу (в общем смысле даже с небольшим положительным градиентом увеличения ресурсов).
Пусть линия регрессии по 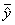 находится на постоянном уровне. Однако техника и технология производства, находясь в неразрывном единстве [4, с.215], влияют на изменение дисперсии отношений. Например, для лесозаготовок это влияние может проявится по сменам работы [5, с.73, с.108, с.118, с.147, с.149].
находится на постоянном уровне. Однако техника и технология производства, находясь в неразрывном единстве [4, с.215], влияют на изменение дисперсии отношений. Например, для лесозаготовок это влияние может проявится по сменам работы [5, с.73, с.108, с.118, с.147, с.149].
В итоге в производственных условиях меняются дисперсии, коэффициенты изменчивости (вариации) и другие статистические показатели нормального распределения, а ненормальные искусственно приводятся постепенно к идеальному (нормальному) закону Гаусса-Лапласа.
Но даже при постоянстве лесных ресурсов, лесной техники и технологии персонал будет стремиться (при внешних социально-экономических условиях) к лучшей организованности, к понижению энтропии функционирования. Поэтому устойчивое развитие лесного предприятия будет наблюдаться как постоянно убывающая скедастическая связь (рис. 2а). Дисперсия или коэффициент вариации будут являться показателями оценки энтропии функционирования и развития (динамика энтропии).
Стремление к устойчивому развитию - это естественный принцип биологических популяций. Например, с возрастом показатель изменчивости таксационных параметров древостоев убывает [6]. Начиная с 30-летнего возраста древостои считаются устойчивыми в ходе роста и далее уже можно выделять кластеры лидирующих, фоновых и отстающих деревьев. При рубках ухода за лесом последние удаляют и используют для заготовки древесного сырья. Аналогично ведет себя популяция ветвей (сучьев) растущего дерева, на котором отстающие ветви находятся внизу кроны и, для повышения качества древесины ствола, их необходимо удалять (уход за деревом).
А вот регуляризация скедастической связи по рис. 2а в корреляционную связь при ![]() или
или 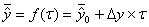 ко всему лесному массиву, нам представляется не совсем корректным. В нашей стране и за рубежом лесоводы стремятся к нормальному лесу. Питер Х. Пирс пишет [7, с.163]: « ... полностью регулируемый нормальный лес редко можно встретить на практике, однако данная теоретическая модель обладает значительным притяжением для лесных менеджеров и ... она является целью, к которой стремится лесное регулирование».
ко всему лесному массиву, нам представляется не совсем корректным. В нашей стране и за рубежом лесоводы стремятся к нормальному лесу. Питер Х. Пирс пишет [7, с.163]: « ... полностью регулируемый нормальный лес редко можно встретить на практике, однако данная теоретическая модель обладает значительным притяжением для лесных менеджеров и ... она является целью, к которой стремится лесное регулирование».
Исходя из результатов лесогеографических исследований можно сделать вывод о том, что модальные леса могут существовать в данной географической зоне, а вот нормальные леса - это только идеальное представление в умах людей.
По-видимому, равномерное по показателю изменчивости распределение участков леса разного возраста практически невозможно хотя бы из разно климатических изменений в течение миллионов лет в одной и той же точке планеты.
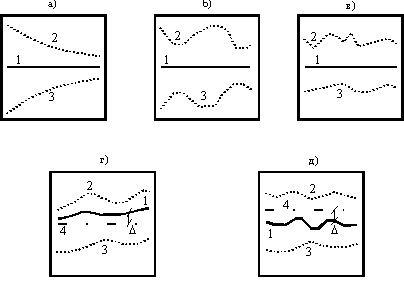
Рис. 2. Скедастичность производственной информации:
а - равномерное усиление организованности производства; б - симметричная волнистая скедастичность; в - асимметричная скедастичность, вызванная изменениями типов законов распределения; г - связь скедастик с прямыми плановыми (нормативными показателями; д - связь скедастик с обратными плановыми (нормативными) показателями; 1 - кривая среднерегрессионного результата; 2, 3 - соответственно верхняя и нижняя границы изменчивости показателей; 4 - уровень планового нормативного) результата; Δ - текущее директивное отклонение фактического результата от планового
Хозяйственное вмешательство, конечно же, должно вести к графику на рис. 2а (опыт лесоводства Швеции и Финляндии), а не наоборот, когда в нашей стране за последние 100 лет скедастическая связь усилилась, то есть изменчивость таксационных показателей повысилась из-за расстроенности и истощенности лесных территорий. Поэтому цель лесного дела по Питер Х. Пирсу [7, с.163] понятна: «Во многих лесных регионах главная проблема регулирования заключается не в том, как управлять нормальными лесами, а как их создать из лесов, имеющих несбалансированное распределение по классам возрастов».
Схема на рис. 2а оказывается фундаментальной для лесной экономики. Если считать начало реформ в лесном деле России с конца 90-х годов, то до 2050-2060 годов (50 лет процесс нормализации лесов шел в Швеции и Финляндии) возможен переход от скедастичности лесоэкономической, лесоводственной и лесотехнической информации к корреляционной.
В этом заключается коренной (физический) смысл изменения содержания и формы в отечественном лесном деле. С начала ХХ века кривые 2 и 3 (рис. 2а) возрастали, а теперь необходим перелом (что требует значительных общих духовно-нравственных усилий всего населения России) и гиперболическое снижение границ изменчивости у показателей лесов и лесной экономики нашей страны.
В итоге получается график биотехнического закона за период более 200 лет (истоки паразитизма лесозаготовок находятся гораздо раньше). Слежение за ходом этой кривой биотехнического развития лесного дела России есть глобальный критерий устойчивого развития (точнее развития к биотехническому равновесию и устойчивости в изменчивости лесного покрова России).
Схема на рис. 2б соответствует нормальному распределению при волнообразном динамизме энтропии функционирования, Цикличность здесь проявляется в среднем через 55 лет (кондратьевские циклы) и даже по другим более крупным периодам. В производстве существуют и меньшие циклы (11, 7 и 3 года). Например, при плановом хозяйстве в течение месяца наблюдается меньшая организованность в начале и большая в конце месяца. В лесном деле включаются еще и фактор сезонности, циклы стихийных бедствий, заболеваний лесов, лесных пожаров, влияния цикла в 26000 лет прецессии оси Земли и др.
В связи с этим для лесных производств при ![]() (рис. 2в) наблюдаются сложные сочетания законов распределения.
(рис. 2в) наблюдаются сложные сочетания законов распределения.
На рис. 2 г,д схематически показаны соотношения плановых (нормативных) и фактических изменений выходного показателя функционирования системы лесного дела (лес, персонал, лесопродукция, оборудование). Например, фондоотдача является прямым показателем, а фондоемкость - обратным. Себестоимость является обратным показателем, а производительность труда на единицу затрат - прямым. Для преодоления негативных свойств затратных экономических методов необходимо перейти к измерению и оценке прямых показателей, в том числе и экологических с помощью инженерных методов.
В связи с этим скедастики по линиям 1, 2, 3 и 4 на рис. 2 г,д - это не просто формальные линии. Они имеют вполне определенный экологический, экономический (и иной) смысл. По свойствам (кривизна, динамика пульсаций и т.д.) этих кривых возможно понять поведение территориальной воспроизводственной системы (по прошлым данным, а значит по линиям регрессии).
Примеры моделирования. Применение биотехнического закона и методики МЭРА покажем на нескольких относительно простых примерах.
Пример 1. Изменение предельной численности популяций сосны в зависимости от возраста A (эта буква общепринята в лесоводстве и лесной таксации для обозначения биологического возраста деревьев, но мы употребляем как изменяющуюся переменную) имеет значение для регулирования густоты лесонасаждений.
По академику В.Н. Сукачеву «жизнь есть беспрерывная борьба за существование» (хотя ныне доказано, что жизнь - это не только борьба, но и симбиотическое взаимодействие). При этом в ходе развития с момента возникновения леса наблюдается удивительное несоответствие между количеством семян и условиями их существования. Например, в урожайном году на одном гектаре может быть рассеяно более двух миллионов семян сосны, а количество семян березы может исчисляться даже десятками миллионов [8, с.7].
По экспертным данным для предельного случая максимальная продуктивность сосны составляет 18 миллионов семян на гектаре леса. А на поливных землях лесопитомников максимальная густота двухлетних саженцев сосны достигает 2 млн. шт./га. По данным [9] в сосняках Сибири найдены участки с молодняком в 34 года с численностью до 900 тыс. шт./га. В максимальном возрасте до 500 лет, по ориентировочным данным, густота популяции сосны достигает
400 шт./га. По этим предельно возможным данным была получена формула
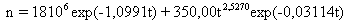 ,(1)
,(1)
где: n - численность популяции сосен, шт./га; t - возраст от нуля до 500 лет. В табл. 1 приведены результаты параметрической идентификации.
Таблица 1. Изменение предельной численности сосен
|
t, лет |
|
n,шт./га |
ε, шт./га |
|
|
0 2 34 500 |
18 106 2 106 9 105 400 |
18 106 2 106 9 105 400 |
0 0.0024 0.0035 0,0004 |
0 0.12 10-6 0.04 10-6 1 10-4 |
Примечание: Δ - относительная погрешность между фактическими и теоретическими (расчетными) значениями численности сосен.
Из данных табл. 1 видно, что формула (1) почти однозначно определяет предельную численность популяции деревьев сосны с изменением возраста. Она содержит две составляющие: во-первых, закон естественной гибели Ципфа-Парето; во-вторых, биотехнический закон возбуждения и гашения жизненных сил популяции в некоторый промежуток возраста. Из уравнения (1) также видно, что популяция (аналогично ведет себя и единичный организм) с некоторого возраста как бы находит в себе силы для циклического возбуждения. Этот факт интересен тем, что циклическое явление возникает на фоне действия закона интенсивного спада у численности популяции.
Это явление можно сравнить с резонатором, когда стандартное распределение силы звука по интервалу частот деформируется на двух сторонах цикла: слева - на фазах зарождения и подъема (участок роста); справа - на фазах упадка и гибели (участок вымирания). Резонаторами являются, например, музыкальные инструменты, создающие циклическое усиление силы звука при распространении в воздухе.
Поэтому в некотором смысле, по аналогии с откликом резонирующего объекта, можем сделать вывод о циклическом законе дополнительного стрессового (резонирующего) возбуждения силы на различных фрагментах цикла взаимодействия.
Пример 2. В книге [67, с.90] приведены данные по влиянию возраста человека на различные его параметры, связанные с действием радиоактивных веществ.
Масса щитовидной железы у человека изменяется по формуле (табл. 2)
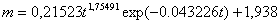 , (2)
, (2)
а эффективный период полувыведения из щитовидной железы радиоактивного йода-131 -
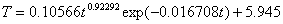 , (3)
, (3)
где t - возраст человека от 0,5 до 70 лет.
Из данных табл. 2 видно, что модели (2) и (3) с очень высокой точностью (практически однозначно адекватные математические модели) описывают параметры человека с изменением возраста. Аналогичные модели были получены и по другим параметрам тела.
Таблица 2. Параметры человека, зависящие от возраста, по поглощаемым дозам радиоактивного йода
|
Возраст t, лет |
Масса щитовидной железы, г |
Период полувыведения, сутки |
||||||
|
|
m |
ε |
Δ, % |
|
T |
ε |
Δ, % |
|
|
0.5 4 14 70 |
2 4 14 20 |
2.0 4.0 14.0 20.0 |
0.0 0.0 3.6e-15 7.1e-15 |
0.0 0.0 2.6e-12 3.6e-12 |
6.0 6.3 6.9 7.6 |
6.0 6.3 6.9 7.6 |
0.0 0.0 0.0 0.0 |
0.0 0.0 0.0 0.0 |
Исходя из двух вышеприведенных примеров можно сформулировать три методологических принципа: во-первых, точность идентификации может оказаться значительно выше точности исходных данных, по которым исследователи получали среднеарифметические (выровненные) значения (чаще всего это происходит при малом количестве наблюдений); во-вторых, если адекватность моделей к фактическим данным высока, то необязательно расчеты выполнять по всем статистическим показателям адекватности, приведенным ранее по классической теории статистики, а достаточно оценить предельные расхождения фактических и теоретических точек; в- третьих, числовые значения параметров моделей необходимо округлять до некоторого количества знаков, в зависимости от точности соответствия моделей исходным данным.
По различному количеству значащих цифр (по мантиссе числа нами рекомендуется: для класса А надежности принять не менее пяти значащих чисел, например 0,23453, или 0,0023453, или 2,34532, или 23,4534, или 234,534; для класса надежности В - не менее четырех значащих чисел).
Второй методологический принцип позволяет существенно сократить трудоемкость анализа показателей статистической адекватности модели, если принять за объект анализа не все исходные наблюдения, а только то наблюдение, которое имеет значение 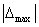 , то есть абсолютное по модулю значение максимальной относительной погрешности в точке.
, то есть абсолютное по модулю значение максимальной относительной погрешности в точке.
Таким образом, в некоторых случаях сознательно требовательность к точности модели увеличивается не менее чем на порядок. Многие примеры моделирования показали, что принятие класса надежности по значению Δ max (максимальная относительная погрешность в какой-то одной точке матрицы данных) гораздо требовательнее к искомым статистическим моделям, чем критерий Фишера χ 2 (хи-квадрат).
Например, при ![]() для малых значений измеряемых величин (лучше сказать о малом интервале изменения измеряемых величин относительно самих величин) получаем класс I (повышенная степень расчетов). Однако доверительная вероятность, при исчислении только по Δ max, а не по всем значениям
для малых значений измеряемых величин (лучше сказать о малом интервале изменения измеряемых величин относительно самих величин) получаем класс I (повышенная степень расчетов). Однако доверительная вероятность, при исчислении только по Δ max, а не по всем значениям 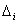 , станет не менее 95%. Поэтому класс надежности опускаем на уровень В (с малым риском). По критерию Фишера окажется, что класс надежности будет приближаться к практически достоверным расчетам, т. е. к 99,7%.
, станет не менее 95%. Поэтому класс надежности опускаем на уровень В (с малым риском). По критерию Фишера окажется, что класс надежности будет приближаться к практически достоверным расчетам, т. е. к 99,7%.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико - математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учеб. пособие / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МарГТУ, 2006. - 326 с.
- Пальчевский, Б.А. Научное исследование: объект, направление, метод / Б.А. Пальчевский. - Львов: Изд-во Львовского университета, 1979. - 180 с.
- Шеремет, А.Д. Анализ экономики промышленного производства / А.Д. Шеремет,
А.В. Прототопов. - М.: Высшая школа, 1984. - 352 с. - Редькин, А.К. Основы моделирования и оптимизации лесозаготовок: Учебник / А.К. Редькин. - М.: Лесн. пром-сть, 1988. - 256 с.
- Мазуркин, П.М. Биотехническое проектирование (справочно-методическое пособие) / П.М. Мазуркин. - Йошкар-Ола: МарПИ, 1994. - 348 с.
- Питер Х. Пирс. Введение в лесную экономику / Пер. с англ.: Учебн. пос. - М.: Экология, 1992. - 224 с.
- Практикум по лесоводству. - М.: Высшая школа, 1989. - 311 с.
- Пшеничникова, Л.С. Продуктивность сосновых молодняков разной густоты // Факторы продуктивности леса / Л.С. Пшеничникова // Сб. научн. трудов. - Новосибирск: Наука, 1989. - С.36-52.




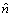 ,шт./га
,шт./га