В работе впервые рассматривается геодезические отображения пространств линейных элементов в терминах присоединенных связностей с кручениями. Пусть 
является пространством линейных
элементов с формой связности 
. С помощью аффинной связности 
, тензора 
и скалярной функции 
в можно ввести следующие объекты присоединенной связности [1] , [2]
(1)
и аффинные пути (обобщенные геодезические кривые)
Пусть 
некоторое другое пространство линейных элементов с формой связности
.
В 
, подобно (1), также можно ввести объекты присоединенной связности 
, 
и аффинные пути
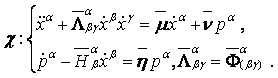
Если пространство отображается на пространство 
с сохранением формы дифференциальных уравнений аффинных 
и 
- путей, то получим следующие преобразования:
, (6)
, (7)
где 
, 
- ковекторы, 
- тензор, причем 
, 
, 
, 
.
Равенство (6), (7) являются основными уравнениями геодезических отображений аффинных , - путей пространств линейных элементов , с кручениями.
Из равенств (6), (7), используя строения объектов (1), находим преобразование для тензора
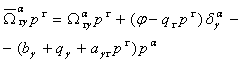, (8)
- являющиеся следствием (6), (7). Свертка (8) с 
приводит к условию 
.
Если связности отображаемых пространств без кручений, то
, ( 9)
Следующие равенства:
, (10)
, (11)
характеризуют проективно точечные пространства линейных элементов, где 
- объект аффинной связности с кручением, зависящей только от координат точки 
, 
. Из (10), (11), при 
, получим связность проективно точечных пространств линейных элементов с кручениями.
Если 
- опорный касательный псевдовектор, то получим уравнение геодезических
, (12)
пространства линейных элементов 
, где 
- присоединенная аффинная связность без кручения.
Следующее преобразование
(13)
сохраняет форму дифференциальных уравнений аффинных Г - путей, где 
, 
.
Формула (13) через объекты связности Картана-Лаптева можно записать так
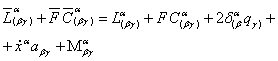,(14)
где 
, 
. Равенство (13), (14) являются однородными нулевого измерения относительно 
.
СПИСОК ЛИТЕРАТУРЫ
- Ферзалиев А.С. О связностях, индуцированных объектами Картана - Лаптева // Publ. Math. Debrecen, 1990, T.37. Fase. 1-2. P.115 - 120.
- Ферзалиев А.С. Пространство линейных элементов присоединенной связности // Изв. вузов. Сер. Математика, 1988, №10, С.55-64.