Рассмотрим гамильтонову функцию одномерной системы
(1)
где x и p - канонически сопряженные переменные, α - малый параметр (α<<1 ). Уравнения движения данной системы можно свести к одному дифференциальному уравнению второго порядка:
, (2)
которое называется уравнением Дюффинга [1]. Методом Линдштедта-Пуанкаре [2] получаем решение уравнения (2) в первом порядке по α
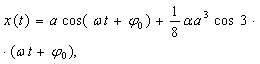(3)
, (4)
. Через 
обозначены корни уравнения
, (5)
где 
- потенциальная функция системы (1), E- полная энергия.
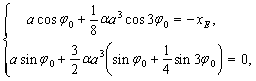
Для определения постоянных интегрирования получаем следующую систему из которой находим, что φ0=0 и 
.
Заметим, что произвольную постоянную при таком выборе начальных условий можно выразить через полную энергию E. Второе слагаемое в скобках в последнем выражении для 
является величиной пятого порядка малости по α, и в рассматриваемом приближении им можно пренебречь. Таким образом, можно считать, что 
и рассматривать как корень уравнения (5). Подставив в выражение (5), и разрешив полученное уравнение методом итераций, найдем выражение через E
В итоге решение (3) в первом порядке по α примет вид
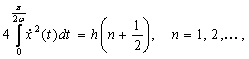
Произведем квантование полученных периодических решений уравнения Дюффинга, отобрав из них те, которые удовлетворяют условию
где 
- постоянная Планка.
Подставив частоту (4), а также выражения для 
и 
в условие квантования, получим
Квантовый аналог гамильтоновой функции (1) получится при помощи известной подстановки 
. Тогда приближенный спектр полученного дифференциального оператора определится по формуле
где 
. Эта формула совпадает с результатом стандартной теории возмущений с точностью до последнего слагаемого во второй скобке. В частности, при 
имеем известный случай гармонического осциллятора.
СПИСОК ЛИТЕРАТУРЫ
- Найфэ А.Х. Методы возмущений. М.:МИР, 1976, 455с.
- Де Брёйн Н.Г. Асимптотические методы в анализе. М.: ИИЛ, 1961, 247 с.
- Давыдов А.С. Квантовая механика. М.: Физматгиз,1963, 748с.