Моделирование играет важную роль для понимания и прогнозирования различных экономических процессов. Эта роль еще более актуализирована тем, что в экономике невозможно проводить многократные эксперименты. Неслучайно, что большинство экономических законов получено эмпирическим путем.
При моделировании в экономике чаще всего используют случайные величины, которые изменяются достаточно сложно, вынуждая применять громоздкие нелинейные модели. Однако предпочитать нелинейную модель более простой линейной не всегда оправдано.
В данной работе представлено моделирование нелинейной случайной величины ( уровень годовой инфляции ) при помощи линейных методов оценки: метода замены переменных. В некоторых случаях для нелинейной зависимости объясняемой переменной от регрессора можно использовать методы линейной оценки для получения достаточно точного прогноза случайной величины. В теории разработан метод, который носит название метода замены переменных. Он заключается в формальной линеаризации некоторых нелинейных корреляционных зависимостей. Для гиперболической :
y = a/x + b,
заменив 1/х новой переменной z можно получить уравнение прямой линии:
y = az + b.
Об эффективности метода замены переменных можно судить по примеру моделирования зависимости годового уровня инфляции в процентах.
В работе выбран период с 1992 - 1995 г.г. Исходный статистический материал взят из журнала « Маркетинг и маркетинговые исследования », октябрь 2002, № 5
Таблица 1.
|
Годы (Х) |
1992 ( 1 ) |
1993 ( 2 ) |
1994 ( 3 ) |
1995 ( 4 ) |
|
Уровень инфляции, % (У) |
2508,8 |
844,2 |
214,8 |
130,6 |
Для сравнения результатов моделирования на первом этапе была использована традиционная форма линейной парной регрессии :
y = ax + b.
С помощью теоремы Гаусса - Маркова были оценены коэффициенты линейной парной регрессии :
a = -776,4 ; b = 2865,6 ,
рассчитан коэффициент детерминации :
R2л = 0,826 ,
и получен прогноз поведения случайной величины ( Рис. 1)
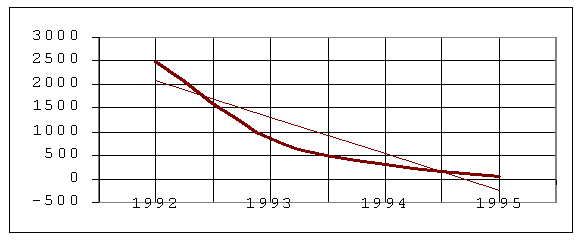
Рисунок 1. Моделирование уровня годовой инфляции
Таблица 2.
|
x |
z |
y |
|
1992 ( 1 ) |
1 |
2508,8 |
|
1993 ( 2 ) |
0,5 |
844,2 |
|
1994 ( 3 ) |
0,33 |
214,8 |
|
1995 ( 4 ) |
0,25 |
130,6 |
Далее с помощью метода замены переменных, где произведена замена 1/х на новую переменную z, исходные данные были переработаны в следующие :
После чего с помощью той же теоремы Гаусса - Маркова были рассчитаны коэффициенты линеаризованной с помощью метода замены переменных модели :
y = az + b,
a = 3274,203 ; b = -780,605 ,
а затем сделан обратный переход, т.е. z заменен на 1/x. Коэффициент детерминации для этой модели составил :
R2н = 0,995 ,
Таким образом можно сделать вывод что метод замены переменных позволяет, оставаясь в границах линейной модели парной регрессии, получить существенно более точную оценку уровня годовой инфляции ( дополнительно объяснено почти 17 % общей дисперсии ).
С другой стороны, форма линейной модели парной регрессии в традиционном виде ( т. е. y = ax + b ) является мало приемлемой для моделирования годовой инфляции, т. к. в конце 1994 года прямая линия пересекает ось абсцисс и значение годовой инфляции становится отрицательным, что в наших условиях противоречит здравому смыслу, тогда как кривая полученная с помощью метода замены переменных все время остается в положительной области значений инфляции.
Прогноз на 1996 год по линейной модели составил : -1020% ; по линеаризованной : 34 %.
Действительное значение годовой инфляции в 1996 году составило 22%. Кок видно из данного примера с помощью метода замены переменных можно не только получить достаточно точную ( R2 = 0,995 ) оценку нелинейных случайных величин, но и строить прогнозы их поведения за границами выборки.



