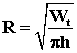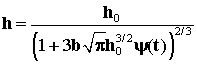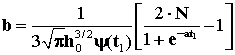По мнению многих исследователей, нефтяная пленка - одна из самых распространенных форм существования нефти как загрязняющего океан вещества [1]. Так, если в морскую воду попало значительное количество нефти, то в течение нескольких часов или, самое большее дней, пятно нефти может охватить много квадратных километров и иметь толщину не более стотысячной доли сантиметра. Поэтому, естественно, возникает необходимость находить размеры и форму нефтяного пятна с течением времени, прогнозировать распространение нефти по акватории и, при необходимости, управлять ее движением.
К настоящему моменту существует более десятка различных моделей, описывающих распространение и растекание нефтяного загрязнения по водной поверхности. В частности, все исследователи, занимающиеся изучением трансформации нефтяных загрязнений, отмечают, как основополагающие, работы Фея [2, 3]. Тем не менее, авторы этих моделей указывают на несовпадение результатов, полученных на основе этих моделей с результатами натурных экспериментов.
Данная работа посвящена построению математической модели растекания нефтяного пятна по водной поверхности и нахождению формы этого пятна.
Сначала найдем закон изменения объема нефти, пролитой на воду, с течением времени.
Общеизвестно, что нефть состоит из тяжелых и легких фракций: W = WТ + WЛ. Легкие фракции достаточно быстро испаряются и растворяются. Тяжелые же фракции значительно в меньшей степени подвержены этим процессам, поэтому можно считать, что объем WТ не испаряется (WТ = const). Кроме того, основываясь на натурных наблюдениях, можно приближенно считать, что в среднем WТ составляет 50 % от объема пролившейся нефти. Помимо этого везде ниже для растекания пятна нефти примем следующую модель (гипотезу): нормальная скорость растекания пропорциональна толщине пятна:
.
Определим закон испарения легких фракций:
При t=0 имеем
.
|
|
(1) |
где W t - объем нефти в текущий момент.
Рассмотрим осесимметричную задачу растекания круглого нефтяного пятна по покоящейся жидкости без учета дрейфа пятна.
В начальный момент пятно нефти представляет собой круг радиуса R0, толщиной слоя h0. Без учета ветра и течения пятно будет, сохраняя форму круга, равномерно растекаться по всем направлениям. Поэтому в текущий момент времени объем нефти W t будет равен 
. Здесь R=R(t) - текущий радиус круга, h=h(t) - текущая толщина слоя.
Отсюда
|
|
(2) |
С другой стороны из закона сохранения массы имеем 
. Здесь 
- скорость опускания верхней границы пятна, левая часть равенства - объем осевшей нефти, правая часть - объем растекшейся нефти по периметру пятна радиуса R, в предположении, что, ввиду малости толщины пятна, нормальная компонента скорости пятна не зависит от толщины пятна, и, что верхняя и нижняя границы пятна плоские.
С другой стороны 
. Здесь знак минус стоит потому, что скорость положительная, а толщина пленки со временем уменьшается (равномерно по всей толщине пятна). Поэтому имеем 
, тогда 
. Подставляя сюда выражение R через объем нефти в текущий момент (2) и гипотезу 
, получаем дифференциальное уравнение для нахождения толщины слоя: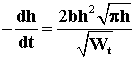 
. Тогда 
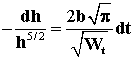. Интегрируя, находим 
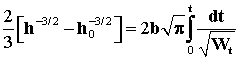где h0 - толщина слоя в начальный момент времени. Итак, имеем: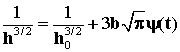 
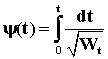
или
|
|
(3) |
Значение b найдем из того факта, что к моменту t=t1 площадь пятна увеличится в N раз: 
. Тогда по (2)
,
,
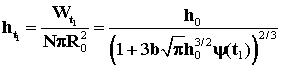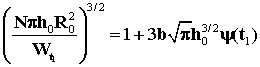то есть,
.
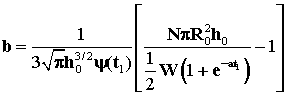А поскольку 
- объем W вылившейся нефти, то получаем
|
|
|
(4) |
Формулы (1)-(4) определяют радиус пятна и его толщину в текущий момент времени.
СПИСОК ЛИТЕРАТУРЫ:
- Войтов В.И., Монин А.С. "Черные приливы". М.: Молодая гвардия, 1984, с.160.
- J.A.Fay "The spread of oil slicks on a calm sea" In: Oil on the sea, Plenum Press. - New-York, 1969, p.53-63.
- Fay J.A. "Physical processes in the spread of oil on a water surface" In: Proc. of Joint Conf. on prevention and control of oil spills. Washington, 1971 (cit. N8).