Знание математической модели процесса позволяет прогнозировать условия изготовления, строение и свойства ткани, оценить степень влияния входных факторов.
Анализ литературы позволил установить, что для математического описания технологического процесса ткачества ранее использовались экспериментальные методы, заключающиеся в обработке экспериментальных данных, полученных в результате реализации математико-статистических методов планирования эксперимента.
Кроме этих методов существуют также методы приближения функций, которые не нашли широкого применения, поскольку требуют проведения значительного количества вычислений, то есть являются очень трудоемкими.
В настоящее время появилась современная вычислительная техника, позволяющая автоматизировать весь процесс исследования какого- либо процесса при наличии всех необходимых для этого средств исследования. Поэтому стало возможным использование методов приближения функций для математического описания технологических процессов.
Сущность методов приближения функций заключается в замене одной функции, которая чаще всего известна лишь эмпирически, другой функцией более простого вида. С этой целью можно применять различные интерполяционные полиномы, в частности, полином Лагранжа.
Для использования этого полинома при исследовании технологического процесса ткачества был составлен автоматизированный алгоритм, в соответствии с которым необходимо:
- На технологическом оборудовании, установленном в ткацком производстве или в лабораторных условиях, с помощью контрольно-измерительных приборов получить диаграмму или осциллограмму натяжения нитей. На диаграмме или осциллограмме выделить участок, после которого цикл натяжения нитей повторяется.
- Для получения дискретной информации об исследуемом процессе разбить диаграмму или осциллограмму натяжения нитей с выбранным постоянным шагом h изменения аргумента.
- На основе экспериментальных данных натяжения произвести вычисления коэффициентов полинома.
- Подставить коэффициенты в полином Лагранжа, общий вид которого:
Р(х) = В0 +В1(х -xо) + В2(х -xо)(х -x1)+ ... + Вп (х -xо)(х -x1)...(x -xп-1)
Для получения диаграммы натяжения нитей основы в лаборатории ткачества кафедры «Технология текстильного производства» Камышинского технологического института (филиал Волгоградского государственного технического университета) был проведен эксперимент на ткацком станке СТБ-2-216.
Полученная в результате эксперимента диаграмма обрабатывалась в соответствии с вышеуказанным алгоритмом. В среде программирования Mathcad было получено несколько математических моделей с различным шагом интерполяции. Оценка эффективности полученных математических моделей производилась в табличном процессоре Excel путем расчета относительной средней квадратической ошибки для всех значений аргумента хi по формуле
,
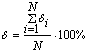где 
- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
,
где 
- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
,
где 
- экспериментальные значения натяжения основных нитей, сН
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
В зависимости от выбранного шага модели имели следующие величины относительной средней квадратической ошибки для всех значений аргумента (см. табл.1).
Таблица 1. Показатели относительной средней квадратической ошибки в зависимости от шага интерполяции
|
Шаг интерполяции |
Величина относительной средней квадратической ошибки на интервале (0; 360 град.), % |
Величина относительной средней квадратической ошибки на интервале (80; 280 град.), % |
|
5 |
84,29 |
100,00 |
|
10 |
68,50 |
81,95 |
|
15 |
84,01 |
96,51 |
|
20 |
47,92 |
46,40 |
|
30 |
21,80 |
7,25 |
|
40 |
37,20 |
2,37 |
|
60 |
3,51 |
3,28 |
|
80 |
10,20 |
5,68 |
|
120 |
10,30 |
5,72 |
Из таблицы 1 видно, что на узком интервале (80; 280 град.) более эффективной математической моделью является та, которая построена с шагом h=40 град. Однако для исследования натяжения нитей на всем интервале эту модель использовать нецелесообразно вследствие большой величины относительной средней квадратической ошибки. В этом случае следует выбирать математическую модель с шагом h=60 град. И в том, и в другом случае величины относительной средней квадратической ошибки на интервале (80; 280 град.) не превышают допустимой нормы δ=5 %, следовательно, математические модели с шагом h=40 и h=60 град. могут быть использованы для прогнозирования изменения натяжения нитей в ткачестве для точек, близких к середине интервала.
Выводы:
- Проанализированы методы приближения функций, которые могут применяться для описания технологических процессов ткацкого производства.
- С использованием полинома Лагранжа получены математические модели натяжения нитей основы при исследовании процесса ткачества и проведена оценка их эффективности.
- Разработаны автоматизированный алгоритм по использованию метода приближения функций с применением интерполяционного полинома Лагранжа для прогнозирования изменения натяжения на ткацком станке и рекомендации по использованию полинома Лагранжа при анализе натяжения в технологическом процессе ткачества.