Методы математического моделирования позволяют прогнозировать и управлять технологическими процессами, строением и качеством тканей, а также определять оптимальные параметры, например натяжение нитей и скорость станка при небольших затратах и достаточно оперативно. Кроме того, методы математического моделирования технологических процессов относятся к числу современных методов и средств исследования и включают в себя методы получения математических моделей и их исследование с помощью электронных вычислительных машин.
Раньше для получения математической модели с целью оптимизации процесса ткачества использовались экспериментальные методы, заключающиеся в обработке экспериментальных данных, полученных в результате реализации математико-статистических методов планирования эксперимента. Использование методов приближения функций являлось нецелесообразным вследствие многочисленных громоздких вычислений, необходимых для получения конечного результата, представленного в виде математической модели. Однако, в последнее время стало возможным использование данных математических методов в связи с тем, что многие расчеты, ранее производимые вручную, сейчас можно автоматизировать, имея соответствующие навыки при работе на современной вычислительной технике.
В работе по использованию математического метода приближения функций с применением полинома Бесселя при анализе технологических процессов ткацкого производства был разработан автоматизированный алгоритм, позволяющий достаточно оперативно получить искомую математическую модель исследуемого технологического процесса и оценить ее эффективность, расчет которой также автоматизирован. Все необходимые вычисления производились в программной среде Mathcad и табличном процессоре Excel.
В соответствии с разработанным алгоритмом необходимо провести эксперимент на ткацком оборудовании с целью получения экспериментальной диаграммы и ее последующей обработки.
На кафедре «Технология текстильного производства» Камышинского технологического института эксперимент проводился на ткацком станке СТБ-2-216, установленном в лаборатории ткачества, при выработке ткани бязь артикула 262. В результате эксперимента была получена диаграмма зависимости натяжения нитей в зависимости от угла поворота главного вала станка.
Для получения дискретной информации об исследуемом процессе полученную
экспериментальную диаграмму натяжения нитей разбили на n интервалов с выбранным постоянным шагом h изменения аргумента. Результатом этого разбиения стало определение значений аргумента и функции в соответствии с выбранным постоянным шагом. Полученные значения функции с выбранным постоянным шагом изменения аргумента были занесены в таблицу экспериментальных данных натяжения нитей, на основе которой составляется таблица разностей.
Для определения коэффициентов полиномa Бесселя из полученной таблицы разностей были выбраны только те значения разностей, которые находятся на линии среднего значения аргумента. Полином Бесселя, в который подставляли все найденные коэффициенты, имеет следующий вид:
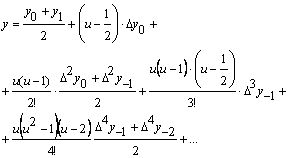
Проведя необходимые преобразования по упрощению полученной математической модели, приступили к определению ее эффективности.
Оценка эффективности математической модели заключается в определении относительной средней квадратической ошибки для всех значений аргумента хi по формуле
,
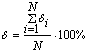где 
- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
,
где 
- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
,
где 
- экспериментальные значения натяжения основных нитей, сН
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
Таблица 1. Показатели относительной средней квадратической ошибки в зависимости от шага интерполяции
|
Шаг интерполяции |
Величина относительной средней квадратической ошибки на интервале (0; 360 град.), % |
Величина относительной средней квадратической ошибки на интервале (80; 280 град.), % |
|
5 |
80,49 |
66,51 |
|
10 |
398,46 |
619,78 |
|
15 |
103,87 |
106,28 |
|
20 |
6644,51 |
11226,90 |
|
30 |
76,24 |
62,83 |
|
40 |
94,11 |
15,30 |
|
60 |
42,79 |
4,81 |
|
80 |
72,39 |
4,82 |
|
120 |
211,98 |
9,27 |
С целью получения более достоверных сведений об исследуемом процессе были построены математические модели с шагом интерполяции h=5, 10, 15, 20, 30, 40, 60, 80, 120 град.
В зависимости от выбранного шага интерполяции математические модели имели следующие величины относительной средней квадратической ошибки для всех значений аргумента (см. табл.1).
Из таблицы 1 видно, что более оптимальной является математическая модель с шагом интерполяции h=60 градусов. Эта математическая модель выглядит следующим образом:
Данную математическую модель можно использовать для контроля натяжения нитей основы на ткацком станке, но только в узких пределах, поскольку особенностью метода приближения функций с использованием интерполяционного полинома Бесселя является то, что применение его дает особую точность для точек, близких к середине интервала.
Выводы:
- Проведен анализ работ, посвященных математическому моделированию технологических процессов ткацкого производства.
- Проанализированы методы приближения функций, которые могут применяться для описания технологических процессов ткацкого производства.
- На основе экспериментальных данных с использованием интерполяционного полинома Бесселя получены математические модели натяжения нитей основы при исследовании технологического процесса ткачества.
- Проведена оценка эффективности полученных математических моделей путем определения относительной средней квадратической ошибки.
- Разработан автоматизированный алгоритм по использованию метода приближения функций с применением интерполяционного полинома Бесселя для прогнозирования изменения натяжения на ткацком станке.
- Разработаны рекомендации по использованию полинома Бесселя при анализе натяжения в технологическом процессе ткачества.