Рассмотрим, о какой катастрофе второго закон Ньютона идёт речь.
Задача
Шарик массой m подвешен на нерастяжимой нити ℓ. Нить равномерно вращается в пространстве, образуя с вертикалью угол α (конический маятник). Определить центростремительную силу F и силу, которая отклоняет шарик от положения равновесия?
Физики предлагают общепринятый вариант (см. рис. 1а).
Решение: Чтобы найти центростремительную силу нужно сложить силы m
и 
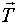по правилу параллелограмма и найти диагональ зная, что равнодействующая этих сил, согласно второму закону Ньютона, направлена по радиусу, но это чистейшая ложь. Второй закон Ньютона в катастрофе, проверим это утверждение экспериментально.
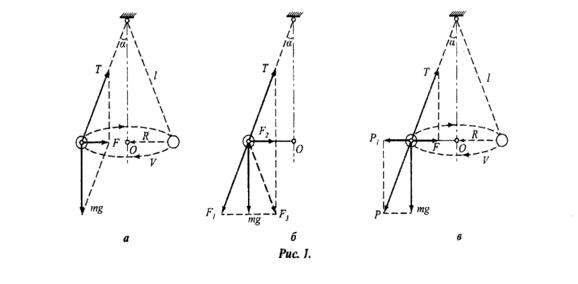
Рассмотрим движение тела массой m по окружности: пять вариантов (см. рис. 2).
Дано: m1 = m2 = m3 = m4 = m5 = m; ℓ - длина нерастяжимой нити; Сила натяжения нити:
F1 при радиусе R1 и скорости V1,
F2 = 2F1 при радиусе R2 и скорости V2,
F3 = 3F1 при радиусе R3 и скорости V3, F4 = 4F1 при радиусе R4 и скорости V4,
F5 = 5F1 при радиусе R5 и скорости V5. Масштаб сил: одна клеточка 0,5 см = 10Н.
Все силы натяжения подтверждаются экспериментально, если скорость шарика увеличивать постоянно. Сила тяжести постоянная, равна mg и она не меняется. Из рис. 2 видно, что у первой массы, с учётом масштаба, F1 = 50H; mg = 40H. По теореме Пифагора центростремительная сила Fц = 30Н и направлена по радиусу. Второй закон Ньютона для этого случая соблюдается. При движении по окружности массы m2, F2 = 100H m = 40H. Центростремительной силы нет, и она не направлена по радиусу. Второй закон Ньютона нарушается. Во всех остальных вариантах второй закон Ньютона нарушается. В физике это называется катастрофой. [1] Рассмотрим общепринятый вариант движения тела по окружности (см. рис. 1б). Из рис. 1б следует, что если слагать вектора по правилам, то результирующая будет равна F3. Это вариант неверный. [2]. Как выйти из катастрофы? Воспользуемся, статьей А.Ростовцева «Один постулат и от силы инерции останется одно воспоминание» [3]. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющие эти тела. Силы не уравновешивают друг друга это третий закон Ньютона F1 = - F2 (1).
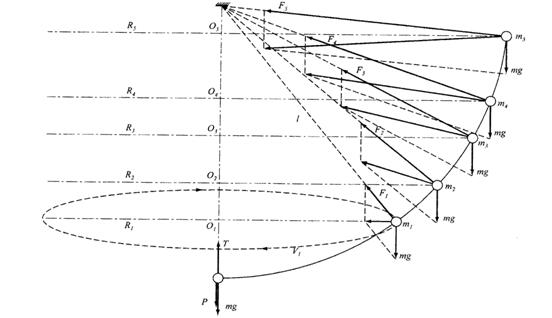
Рис. 2.
Если F1 = F2 = mа (2), где m - масса тела, а - ускорение, то уравнение (1) запишется так:
m а = - m а (3), откуда а = - -а (4).
Физический смысл уравнения (4) только одному богу известен, поэтому придадим этому уравнению свой физический смысл с введением постулата.
Постулат. Любая материальная точка, движущаяся с ускорением, создает инерционное (гравитационное) поле, равное ускорению и противоположно ему направленное. Инерционное поле, в отличие от гравитационного, не взаимодействует с материальными точками и телами.
Иными словами, используя постулат, в неинерциальных системах отсчета, расположенных вблизи Земли, можно применять те же законы, формулы и уравнения, что и в инерциальных, но всюду, где стоит вектор g0, заменить его вектором g, равным g = g0 + (- а) (5) , где g0 -- ускорение свободного падения вблизи Земли, (-а) - инерционное поле.
Вес - сила, с которой тело, притягиваясь к Земле, действует на опору или натягивает нить подвеса. P = mg. (6). Подставляя уравнение (5) в уравнение (6) получим:
Р = m [ g0 + ( - а) ] (7).
Если а = 0 , то вес равен силе тяжести: Р = m g0 (8) [4].
Рассмотрим эту теорию на примере (см.рис.1в).На тело действует сила тяжести m g и сила натяжения нити Т, результирующая этих сил равна F ц = m а, согласно постулата масса образует инерционное поле (-а) , тогда вес тела будет равен Р = m [ g0 + (-а) ] и он приложен к нити Из всего сказанного делаем резюме: законы Ньютона справедливы как в инерциальных , так и в неинерциальных системах отсчета, Что касается силы инерции, то ее заменяет одна из составляющих веса тел Р1.
Английский философ и логик Оккам (1285-1349) различал интуитивное знание, связанное с восприятием и переживанием единичной вещи, и абстрактное знание, которое способно отвлекаться от единичного. Известный принцип Оккама («бритва Оккама»), гласящий, что «не следует множить сущности без надобности», вошёл в сокровищницу человеческой интеллектуальной мысли, означает, что каждый термин обозначает лишь определенный предмет [5].
Рассмотрим с точки зрения диалектики понятия: равенство и уравнение. Это абсолютно два разных понятия. Пусть на материальную точку m действуют две равные и противоположно направленные силы F1 и F2 .для них имеет место равенство: F1 = - F2 (9). Если результирующая этих двух сил равна нулю, тогда F1 + F2 = 0 это, во- первых , уравнение и представляет собой первый закон Ньютона, а значит инерциальную систему отсчета. Пусть две материальные точки m1 и m2 движутся навстречу друг другу и сталкиваются, для них имеем место равенство
F1 = - F2 (10), это третий закон Ньютона. По форме уравнения (9) и (10) идентичны, а по содержанию нет. У третьего закона Ньютона нет равнодействующей потому, что силы приложены к разным телам, а, следовательно, это не уравнение, а векторное равенство. Уравнение и равенство - понятия разные [6].
Нельзя делать равенство между вектором и скаляром, это все равно, что приравнять мужчину к жеребцу по половому признаку. Все уравнения, где одна часть векторная, а другая скалярная должны записываться только по модулю: «Закон всемирного тяготения», «закон Кулона » и т.д.
Рассмотрим закон всемирного тяготения, установленный Ньютоном Согласно этому закону, любые две материальные точки взаимодействуют с силой пропорциональной произведению их масс (m1 и m2) и обратно пропорциональной квадрату расстояния r между ними:
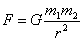(11), где G - гравитационная постоянная.
Правая часть уравнения (11) - векторная, левая - скалярная, поэтому их нельзя приравнивать. Во-первых, это противоречит понятиям вектор, скаляр. Во-вторых, в формуле (11) отсутствует третий закон Ньютона, а взаимодействие происходит по третьему закону Ньютона. В-третьих, если уравнение (11) записано по модулю, то будьте добры, господа физики, поставить знак модуля.
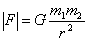(12), откуда 
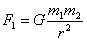(13) и 
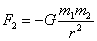(14).
Если правые части равенств (13) и (14) равны по модулю, тогда равны и левые по векторам F1 = - F2 , а это и есть третий закона Ньютона, выведенный из закона всемирного тяготения .Переход от векторной записи к скалярной определяется теоремой косинусов, но Шероварченко Г.А считает, что отрицательных чисел в природе не существует. Любые отрицательные ответы имеют физический смысл., т.е. это два вектора равных по модулю но противоположных по направлению [6]. В третьем законе Ньютона нет равнодействующей, поэтому, чтобы перейти от векторной записи закона к скалярной возведем обе части равенства (1) в квадрат получим F12 = F22 или F12 =±
откуда F = F2 (15) и F1 = - F2 (16) Учитывая уравнения (2) уравнения (15) и (16) будут выглядеть так
F = m а (17) и F = - m а (18), уравнение (17) это второй закон Ньютона, а уравнение (18) это закон инерции. Отсюда делаем вывод, что третий закон Ньютона это всеобщий закон природы в который входят: первый закон Ньютона, второй закон Ньютона и закон инерции. Так как эти законы являются частными случаями третьего закона Ньютона, они не законы, а закономерности. Любой исследователь может попасть в ловушку, созданную природой. Он не должен путать: закон с закономерностью, закономерность - со случайностью зная, что закономерность это частный случай закона, в то время, как случайность это единственный случай закономерности.
СПИСОК ЛИТЕРАТУРЫ
- Статья: А.К. Ростовцев «Классическая физика на гнилом фундаменте (катастрофа в механике» в журнале «Успехи Современного Естествознания». М.: Академия Естествознания. №3, 2009г, с.7.
- Балаш В.А. Задачи по физике и методы их решения. - М.: Просвещение, 1983. - с.69.
- Статья: А.К.Ростовцева «Один постулат и от силы инерции останется одно воспоминание», в журнале: «Европейская Академия Естествознания» (Лондон) 2007 г. №6, с. 146, на английском языке.
- Статья: «Один постулат и от силы инерции останется одно воспоминание», научно- теоретическом журнале: «Успехи Современного Естествознания» №3, 2008. с.69.
- Статья: А.К. Ростовцева «Философия в мире наук», «Международный журнал прикладных и фундаментальных исследований» №3, 2009Г, С. 133.
- «Философия науки», В.П. Кохановский, Т.Г. Лешкевич, 2007, с. 73, 67.
- Статья: Г.А. Шероварченко, А.К. Ростовцев: «Математический и физический смысл отрицательных чисел» журнал «УспехиСовременногоЕстествознания» №7, 2008, с.109.