Практически любой опасный промышленный объект подвергается неуправляемым и управляемым воздействиям. К первому виду воздействий относятся неблагоприятные природные влияния, неквалифицированные действия персонала, нарушение технологии эксплуатации и так далее. Задача управляющих воздействий состоит в поддержании промышленного объекта в состоянии, позволяющем отражать неблагоприятные воздействия, то есть сохранять определенный уровень стойкости промышленного объекта.
Увеличивая затраты на управляющие воздействия, можно достичь достаточно высокого уровня стойкости и свести потери от неблагоприятных воздействий до минимума, либо, проводя минимум управляющих мероприятий (экономя на затратах), получить большие потери в стойкости промышленного объекта. Очевидно, что здесь необходима оптимизация по минимуму общих потерь при эксплуатации опасного промышленного объекта. Исследуем возможность применения при этом модели в виде системы массового обслуживания (СМО).
В схеме метасистемы, функционирующей в данном случае как СМО на вход системы (сверху) поступают с интенсивностью λ неблагоприятные воздействия. Причем каждый из промышленных объектов реагирует на эти воздействия по-разному: для одних наиболее опасны природные воздействия, для других неквалифицированные действия персонала, либо изменение экономической обстановки или даже угроза террористического акта. Поэтому можно разбить промышленные объекты на классы в соответствии с их восприимчивостью к воздействиям и считать, что каждый класс реагирует только на свои воздействия и не замечает других. Например, хладостойкость важна для опор линий электропередач в Сибири и практически не требуется для резервуара под давлением находящегося в отапливаемом помещении.
При этих оговоренных условиях метасистему можно рассматривать как совокупность одноканальных СМО с отказом. Каждый из объектов класса характеризуется стойкостью, измеряемой интенсивностью воздействий, которые он может отразить - μ. Если интенсивность поступления неблагоприятных событий превышает стойкость, имеют место потери от каждого пропущенного неблагоприятного воздействия. В соответствии с классической теорией СМО вероятность обслуживания заявки (отражения неблагоприятного воздействия) равна
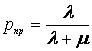
С другой стороны, чем выше должна быть стойкость объекта, тем больше необходимо произвести затрат управляющих воздействий. Пусть коэффициент пропорциональности при этом равен α.
В качестве критерия необходимо рассматривать суммарные потери от неблагоприятных воздействий и затраты управляющих воздействий. Поскольку каналы СМО в данном случае независимы, то необходимо минимизировать такой критерий для каждого i-го класса объектов
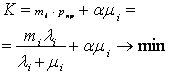
где: mi - потери от неотраженного отрицательного воздействия; 
- коэффициент пропорциональности. Дифференцируя этот критерий по μ и приравнивая производную нулю, можно найти оптимальную стойкость каждого из классов промышленных объектов.