Введение. Эра космонавтики дала возможность современным технологиям оторваться от поверхности Земли и осваивать околоземное пространство. То, что невозможно сделать в условиях земного притяжения, - в невесомости космического пространства вполне реально. Так родилась новая наука - космическое материаловедение, появились первые сверхчистые материалы - полупроводниковый германий с процентным содержанием вещества 99,9999% и выше [1].
В 1975 году усилиями американских и канадских специалистов в условиях строжайшей секретности была создана космическая лаборатория для получения сверхтонких оболочек из монокристаллов. Предполагаемая прочность выращенной в космосе оболочки должна была по оценкам экспертов на два порядка превзойти аналогичную поликристаллическую. Однако реальная прибавка прочности оказалась намного скромнее [7].
Преградой на пути революционно новых технологий стали микроускорения, поле которых образуется внутри космического аппарата (КА) от различного рода внешних (притяжение Земли, аэродинамическое сопротивление и др.) и внутренних (работа управляющих ракетных двигателей (УРД) системы ориентации КА, другого оборудования КА и др.) воздействий. Изучение, прогнозирование и обеспечение необходимого для технологического процесса уровня микроускорений стало одной из важнейших проблем космического материаловедения и объединило усилия ученых всех космических держав мира [8] .
Дорогостоящие натурные испытания не всегда оправдывают затраты, поэтому важную роль в современных условиях играет моделирование микроускорений [7]. Это объясняется двумя основными причинами. Во-первых, измерительная аппаратура, которая должна фиксировать значения порядка 10-6 испытывает на старте значительные перегрузки. Поэтому стоит осторожно относиться к обработке экспериментальных данных. Например, в работе [6] приведены обработки замеров уровня микроускорений на борту ИСЗ ФОТОН 11 с помощью французских акселерометров ВЕТА. Авторы работы указывают на возможное неправильное использование программного обеспечения, т.к. в приведенных графических зависимостях различных компонент микроускорения от времени имеется большое постоянное смещение. Хочется отметить также, что, согласно этим измерениям, первая компонента имеет максимальное значение порядка 1,6x10-4 м/с2, вторая - 5,7 x10-3м/с2, а третья - 3,1x10-3м/с2. Хотя никаких причин для такого отличия в значениях (более, чем в 20 раз), кроме отказа аппаратуры, на мой взгляд, нет.
Во-вторых, микроускорения нельзя измерить в чистом виде, - измеряются величины, которые влияют известным образом на их значения. Существуют различные методики получения зависимости микроускорений от времени. В работе [4] рассмотрен способ определения микроускорений с помощью датчика конвекции «Дракон», который был изготовлен в Пермском государственном техническом университете и в течение двух лет испытывался на орбитальной станции МИР. В работе [2] приводится целый ряд измерений микроускорений на ИСЗ от ФОТОН 2 (1986 год) до ФОТОН 10 (1995 год), а также ФОТОН 11 ( 1997 год ) и ФОТОН 12 (1999 год). Для этой цели конструкторским бюро общего машиностроения им. В.П.Бармина (г. Москва) был разработан комплекс технологических установок УЗ01, УЗ04, ПОЛИЗОН с системами измерения малых ускорений СИУ01,СИУ02 и СИУ03, а на двух последних космических аппаратах ( КА ) применялась аппаратура QSAM, разработанная специалистами германского центра DLR, и вышеупомянутая французская аппаратура ВЕТА. В работе [5] дано сравнение результатов расчета квазистатической составляющей микроускорений, полученных несколькими методами оценки.
Из всего этого обширного исследовательского материала можно сделать один вывод - даже при обработке экспериментальных данных строятся математические модели. На мой взгляд, здесь нет чистого классического эксперимента. Если угловую скорость, например, можно измерить в чистом виде с помощью датчиков угловых скоростей, то в случае с микроускорением понимание картины происходящих процессов изменения поля микроускорения даже квазистатической его компоненты приходит только после математического моделирования полученных экспериментально результатов.
Все вышесказанное несколько нивелирует роль натурных испытаний, отдавая пальму первенства математическим моделям. Эксперименты, в свою очередь, могут служить подтверждением или опровержением теоретических гипотез и положений.
Постановка задачи. В данной работе проведены исследования функции распределения изменения уровня микроускорений как случайной величины. Эти исследования важны для прогнозирования микроускорений с помощью фрактальной функции Вейерштрасса-Мандельброта еще на этапе проектирования КА, когда ни о каких натурных испытаниях не может быть и речи [7, 8].
Пусть орбитальный КА представляет собой центральное тело и большие упругие элементы: две панели солнечных батарей (ПСБ) и одну панель радиатора [1]. В качестве возмущающего фактора, подпитывающего поле микроускорений, в использованной математической модели предлагается выбрать момент от управляющих ракетных двигателей (УРД) системы ориентации (СО) КА. Это связано с тем, что основной вклад в квазистатическую составляющую микроускорений вносит движение КА вокруг центра масс, как считают многие исследователи. Действительно, гравитационная и аэродинамическая возмущающие компоненты могут быть почти полностью нивелированы за счет увеличения высоты орбиты КА, тогда как на движение вокруг центра масс этот шаг напрямую не повлияет. Включение УРД СОКА вызывает значительный скачок уровня микроускорений, однако, обойтись них на данном этапе развития космической техники невозможно. Есть другой выход - все технологические процессы, требующие жесткого выполнения условий микрогравитационного штиля (ограничение на квазистатическую составляющую около 1,0x10-6м/с2), проводить между включениями УРД, широко используя пассивную ориентацию КА (маховичные системы и т.д.). Поэтому предлагается смоделировать следующую ситуацию: на КА были включены УРД для его ориентации. Считается, что все двигатели СО создают равный по модулю момент. Такое возмущение вызывает колебания больших упругих элементов, которые поддерживают своим движением поле микроускорений после выключения УРД.
Здесь важно правильно определить тот момент времени, когда затухающие за счет внутреннего демпфирования колебания упругих элементов, будут порождать микроускорения, допустимые требованиями технологического процесса. Именно с этого момента и можно начинать эксперименты. Теоретический учет демпфирования предлагается проводить по классической схеме «вязкого трения» [3]. Фрагмент изменения уровня микроускорений во времени, полученный с помощью модели [1], которая основана на вышеописанных предположениях, представлен на рис. 1. Здесь логарифмический декремент колебаний принимался равным 0,1 [10], а максимальный момент от УРД - 1 Н м.
Статистические исследования. Максимальный уровень микроускорений при данных условиях моделирования составил 1,44 мкм/с2, т.е. полный диапазон изменения модуля микроускорений - 0...1,44 мкм/с2. Этот диапазон был разбит на восемь равных отрезков. С равномерным шагом t = 0,01 c. проводилась выборка значений микроускорений. Нетрудно заметить, что благодаря демпфированию число точек, попадающих во все отрезки диапазона, кроме включающего ноль (первый отрезок), ограничено и всегда можно найти такой момент времени, после которого ни одна точка не попадет в этот отрезок. На практике колебания упругих элементов прекращаются за конечный, пусть и значительный отрезок времени, т.е. число точек, попавших в первый диапазон, также ограничено. При моделировании демпфирования колебаний «вязким трением» нулевое значение микроускорений достигается лишь при ![]() . Поэтому при неограниченном увеличении выборки неограниченно возрастает и число точек, попадающих в первый диапазон.
. Поэтому при неограниченном увеличении выборки неограниченно возрастает и число точек, попадающих в первый диапазон.
Исследование функции распределения этой случайной величины показало, что при увеличении выборки она стремится к гамма-распределению. После получения экспериментальных функций распределения с помощью прикладного математического пакета «Statistica 6.0» было подобрано гамма-распределение [9]. На рис. 2 показано изменение суммы квадратов отклонений теоретической и эмпирической функций распределения. При расчетах гамма-функция аппроксимировалась многочленом восьмого порядка с точностью 3х10-7 [9].
Основные результаты работы. В результате исследований показано, что функция распределения микроускорений во времени стремиться к гамма-функции при наличии демпфирования. Выявлен ряд характерных точек: начиная с момента времени 141,53 с. все точки попадают только в первый диапазон (0...0,18 мкм/с2), начиная с момента времени 142,61 с. в первом диапазоне оказывается самое большое число точек. Примерно до 150 с. все выборки следует считать малыми. Они характерны хаотичным изменением параметров функции распределения. Критерий согласия хи-квадрат Пирсона позволяет использовать гамма-распределение на 10%-м и ниже уровнях значимости для любой, в том числе и малой выборки, в качестве функции распределения уровня микроускорений во времени.
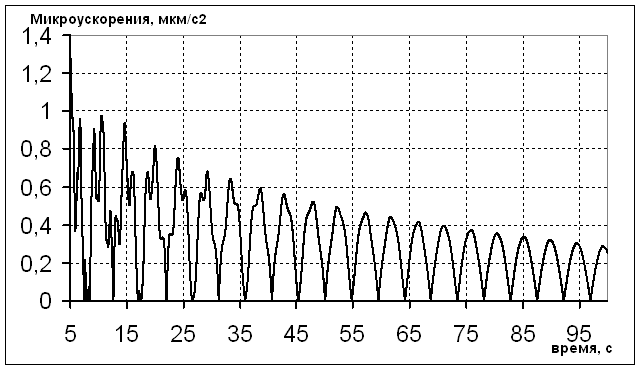
Рисунок 1. Фрагмент зависимости модуля микроускорений от времени после выключения УРД (t = 5 с.)
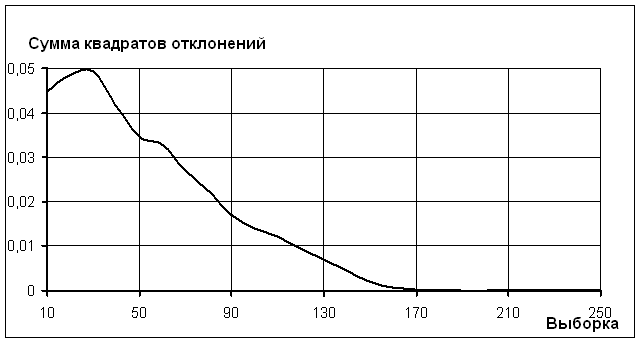
Рисунок 2. Зависимость суммы квадратов отклонений теоретической и экспериментальной функций распределения от размера выборки
СПИСОК ЛИТЕРАТУРЫ
- Авраменко А.А, Седельников А.В. // Изв. вузов Авиационная техника. 1996. №4. с. 22 - 25.
- Бармин И.В., Волков М.В., Егоров А.В., Реут Э.Ф., Сенченков А.С. // Космические исследования. Т. 39. № 4. 2001. с. 407-418.
- Нашиф А., Джоунс Д., Хендерсон Дж. Демпфирование колебаний М.: Мир. 1988. 448с.
- Никитин С.А., Полежаев В.И., Сазонов В.В. // Космические исследования. Т. 39. № 2. 2001. с. 179-187.
- Сазонов В.В., Беляев М.Ю., Ефимов Н.И., Стажков В.М., Бабкин Е.В. // Космические исследования. Т. 39. № 2. 2001. с. 136-147.
- Сазонов В.В., Чебуков С.Ю., Абрашкин В.И., Казакова А.Е., Зайцев А.С. // Космические исследования. Т. 39. № 4. 2001. с. 419-435.
- Седельников А.В., Бязина А.В.// Сборник научных трудов в Самарском филиале УРАО. вып. 2-3. Самара. 2002. с. 72 - 85.
- Седельников А.В., Бязина А.В., Антипов Н.Ю. // Сборник научных трудов X Всероссийского научно-технического семинара по управлению движением и навигации ЛА. Самара. 2002. с. 124-128.
- Титов Б.А., Вьюжанин В.А., Дмитриев В.В. Формирование динамических свойств упругих космических аппаратов М.: Машиностроение. 1995. 304 с.
- Справочник по специальным функциям // п/р Абрамовица М. и Стиган И. М.: Наука. - Главная редакция физико-математической литературы. 1979. 832 с.



