Под идеальным рынком авторы понимают рынок, удовлетворяющий следующим условиям:
- На рынке предлагается абсолютно идентичная продукции, но в разных объемах на разных ценовых уровнях (по разной цене), при этом цена продукции - это единственное, что отличает конкурентов;
- Между собой случайно взаимодействуют единицы спроса и единицы предложения, т.е. каждый покупатель хочет приобрести одну единицу продукции, и каждый продавец продает только одну единицу продукции;
- Ни одна единица спроса и не одна единица предложения не может перейти из одной ценовой категории в другую;
- За время взаимодействия общей совокупности спроса и предложения на рынок не поступает ни новых единиц предложения, ни новых единиц спроса;
- Взаимодействие единиц спроса и единиц предложения идет до тех пор, пока больше произойти сделок не может;
- Исследователь имеет достоверную информацию о рынке;
Допустим в результате маркетингового исследования были получены данные о предложении идентичной продукции и спросе на неё на идеальном рынке.
На рынке возможна встреча единицы любого уровня спроса и единицы любого уровня предложения. Если допустить, что суммарный спрос, равен суммарному предложению, и в какой-то момент времени любая единица спроса встретилась с единицей предложения, причем каждая единица спроса встретилась только с одной единицей предложения и наоборот, то факт полной встречи можно представить в виде таблицы, далее называемой таблицей расклада
Например, в таблице 1.
- количество встреч единиц 3-го ценового уровня спроса и 2-го ценового уровня предложения. На главной диагонали таблицы и под ней отражены сделки, а над ней несделки, т.е. встречи соответствующих уровней спроса и предложения без сделок. Формирование сделочной и несделочной зоны таблицы обусловлено тем, что предложение i-го уровня может быть реализовано за счет спроса уровней [i;n] и соответственно спрос j-го уровня может быть отоварен за счет предложения уровней [1;j]. Подобное явление связано с тем, что лимитирующим фактором для любой сделки является цена и спрос по цене j может отовариться только за счет j-го же предложения или за счет предложения с более низкой ценой (т.е. более низкого ценового уровня), что так же его устроит, поскольку продукция идентична.
Таблица 1. Таблица расклада
|
|
|
|||||
|
|
j i |
1 |
2 |
3 |
... |
N |
|
1 |
|
|
|
... |
|
|
|
2 |
|
|
|
... |
|
|
|
3 |
|
|
|
... |
|
|
|
... |
... |
... |
... |
... |
... |
|
|
n |
|
|
|
... |
|
|
Вероятность таблицы расклада в случае равенства спроса и предложения можно найти по формуле:
при этом в данной формуле 
- это и варианты сделок и варианты встреч, т.е. ячейки таблицы полученного расклада, а k - это номер таблицы расклада. Рэл - вероятность элементарного события, т.е. какой-то единичной таблицы расклада (дробь на которую умножается Рэл - соответственно количество способов, получения данного расклада). Очевидно, что при равенстве суммарного спроса и предложения 
для всех вариантов расклада. Для варианта 
формула расчета вероятности таблицы расклада будет иметь вид:
Некоторые таблицы расклада представляют модель такой ситуации на рынке, что более ни одной сделки произойти не может (конечная таблица расклада). Ситуация невозможности сделки можно считать стабильной. Все прочие рыночные ситуации стремятся к состоянию стабильности. Любая неконечная рыночная ситуация (т.е. когда возможны ещё сделки) стремится стать конечной, и неизбежно перейдет в неё. Требуется определить условие конечности.
Необходимое условие конечного варианта (таблицы расклада).
Существует для некоторых уровней спроса такая часть спроса, которая обязательно отоварит (свершится сделка) некоторую часть предложения при любом раскладе на рынке. Назовем эту величину min 
.
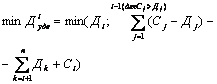(2.5)
Т.е. некоторый спрос Дi однозначно может отоварить предложение Сi и то предложение, которое останется избыточным для уровней 1...i-1 (суммарное по ценовым уровням, где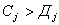 
, а не (
), поскольку i-ый уровень спроса не претендует на i+1 уровень предложения), при условии, что i=n. Но, если i≠n, то при «наихудшем» раскладе это предложение может быть отоварено за счет уровней 
.
Однако если < 
,
то разница между правой и левой частями уравнения и будет величиной предложения, которую минимум удовлетворит спрос Дi. Эта величина (разница) для уровней спроса близких к n может быть больше Дi, поэтому и используется оператор min.
Достаточное условие.
можно считать и достаточным условием, только в том случае, если предложение 
было отоварено 
. Однако, вполне возможен вариант, что потенциально реализуемое предложение, предназначенное для i-го уровня спроса, занято (первая встреча) спросом более низких уровней, не способных к покупке. И такая ситуация может возникнуть относительно части спроса Дi , при этом реализованная часть, возможно, будет больше .Очевидно, что даже при таких условиях предложение при следующем раскладе имеет возможность реализоваться, что и является показателем неконечности варианта.
Соответственно достаточным условием для некоторого спроса Дj можно считать
(2.6)
В случае, если вышеприведенная формула не дает верного результата, то достаточным условием можно считать:
(2.7)
Однако если выполняется формула
, то выполнение формулы
не обязательно.
Соответственно, только если на всех уровнях спроса выполняется достаточное условие (а значит и необходимое), вариант в целом можно считать конечным.
Таблиц расклада, если в каждой ценовой категории представлено несколько видов однородной продукции (что обычно и наблюдается на реальном рынке) будет выглядеть следующим образом
Таблица 3. Макет таблицы расклада
Соответственно l - номер изделия из совокупности однородной продукции. Найти вероятность таблицы расклада соответственно, в случае, если можно по формуле:
Достаточным условием конечного расклада для спроса Дj в подобного вида раскладах можно считать условие
В случае, если вышеприведенная формула не дает верного результата, то достаточным условием можно считать:
Однако если выполняется формула
, то выполнение формулы
не обязательно.
Соответственно, только если на всех уровнях спроса выполняется достаточное условие (а значит и необходимое), вариант в целом можно считать конечным.
СПИСОК ЛИТЕРАТУРЫ
- Вентцель Е.С. Теория вероятностей. // М.: Высшая школа, 2002.
- Гмурман В.М. Теория вероятностей. Учебник для ВУЗов.// М.: Высшая школа, 2003.
- Евтодиева Т.Е. Логистические основы процесса сбытовой деятельности// Самара, СГЭА, 2000.
- Клёнов М.В., Ольшанский А.М. Структура и динамика выпуска продукции. Расчет, анализ и прогноз совокупного спроса в Самарской области// Самара, 2002.