Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в ПСКВ позволяют существенно повысить скорость вычислительных устройств ЦОС. Кроме того, применение модулярных полиномиальных кодов позволяет повысить надежность функционирования вычислительных устройств, входящих в состав современных систем управления
Проблема обеспечения надежного функционирования сложного вычислительного устройства, в настоящее время приобретает первостепенное значение. Применение избыточного модулярного кодирования является одним из перспективных направлений обеспечения устойчивости к отказам, поскольку позволяют обнаружить и исправить ошибки, вызванные неисправностями оборудования.
Доказанные в работе теоремы [1] служат основой процедур поиска и исправления ошибок на основе проекции модулярного кода. Характерной чертой данного метода контроля является возможность коррекции ошибки даже при минимальном числе избыточных оснований. Так наличие одного контрольного основания, удовлетворяющего условию
![]()
позволяет однозначно исправить последствия однократной ошибки по любому основанию ПСКВ.
Однако, как показывают исследования [1-3], реализация данного метода характеризуется значительными схемными затратами, необходимыми для осуществления обратного преобразования из ПСКВ в позиционный код с последующим сравнением с величиной рабочего диапазона. В этом случае схемные затраты составят
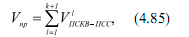
где Vt ПСКВ-ПСС - схемные затраты, необходимые на реализацию обратного преобразования из модулярного кода в позиционный код в ПСКВ, заданной основаниями {pj(z)},j≠l, j=1,2...k+1;l=1,2...k+1.
Исходя из условия, что техническое выполнение процедур поиска и коррекции ошибок в модулярном коде тесно связано с устойчивостью функционирования СП класса вычетов, очевидно, что устройство определения и локализация ошибки, состоящее из меньшего количества комплектующих элементов, оказывает меньшее воздействие на снижение надежности функционирования СП СПКВ. Данное положение полностью согласуется с экспоненциальной моделью надежности, в которой интенсивность отказов вычислительного устройства пропорционально суммарному числу элементов, из которых оно состоит.
Тогда математическая установка задачи выбора реализации процедуры поиска и коррекции ошибок в модулярном коде имеет вид
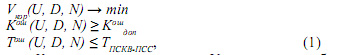
где Укор - схемные затраты; U - алгоритм обнаружения и коррекции ошибок в молекулярных кодах; D - пространственно-временное разделенеи алгоритма в нейросетевом базисе; N - набор модулей полиномиальной системы классов вычетов; Kош - количество парируемых ошибок выбранным алгоритмом; Kошдоп - минимально допустимое количество обнаруженных и исправленных ошибок; Тош - временные затраты необходимые на реализацию процедуры поиска и коррекции ошибки; Тпскв-псс - временные затраты на обратное преобразование из модулярного кода в позиционный код.
В табл. 1 представлены исходные данные, необходимые для решения поставленной задачи для СП ПСКВ, функционирующих в расширенных полях Галуа GF(23), GF(24), GF(25).
Табл. 1. Исходные данные для выбора алгоритма коррекции ошибок
|
№ п/п |
Алгоритм поиска и исправления ошибок |
Кратность ошибки |
Затраты на реализацию алгоритма |
|||
|
аппаратурные (нейроны) |
временные (кол-во итераций) |
|||||
|
GF(23) |
GF(24) |
GF(25) |
||||
|
1 |
Параллельная нулевизация [1] |
1 |
15 |
40 |
85 |
1 |
|
2 |
Интервальный номер [1] |
1 |
17 |
52 |
139 |
1 |
|
3 |
Интервальный номер [3] |
1 |
14 |
47 |
130 |
2 |
|
4 |
Коэффициенты ОПС [1] |
1 |
14 |
67 |
197 |
1 |
|
5 |
Синдром ошибки [2] |
1 |
18 |
41 |
87 |
1 |
|
6 |
Спектр [1] |
1 |
23 |
84 |
188 |
2 |
Анализ таблицы 1 показывает, что оптимальным способом реализации немодульной процедуры определения, локализации и исправления ошибки для конвейерной структуры СП ПСКВ с двумя контрольными основаниями, удовлетворяющим предельной теореме представленной работе [1], является метод параллельной нулевизации. Данный метод реализуется при этом минимальных аппаратурных и временных затрат.
Однако, если учитывать то обстоятельство, что коэффициенты обобщенной полиадической системы (ОПС) используется при выполнении процедур перевода непозиционного кода ПСКВ в позиционную систему счисления, то при проведении сравнительного анализа необходимо учитывать и схемные затраты необходимые для обратного преобразования на основе КТО. Тогда получаем, что для реализации процедуры поиска и локализации ошибки при переводе кода ПСКВ в ПСС на основе параллельной нулевизации потребуется:
- для поля GF(23) 49 формальных нейронов;
- для поля GF(24) 166 формальных нейронов;
- для поля GF(25) 401 формальных нейрон.
На рисунке 1 приведен сравнительный анализ двух методов определения глубины и местоположения ошибок в кодах ПСКВ с учетом аппаратурных затрат на устройство обратного преобразования ПСКВ-ПСС для различных полей Галуа GF(25).
Из рисунка 1 наглядно видно, что применение алгоритма вычисления коэффициентов ОПС позволяет обеспечить более надежную работу устройства обнаружения и коррекции ошибок по сравнению с параллельной нулевизацией. Полученные результаты показывают, что для СП класса вычетов с двумя контрольными основаниями алгоритм вычисления коэффициентов обобщенной полиадической системы, представленный в работе [1], является оптимальным. При этом при дальнейшем увеличении разрядной сетки СП ПСКВ с параллельно-конвейерной организацией вычислений эффективность применения данного алгоритма возрастает.
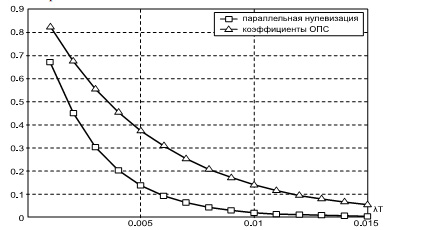
Рис. 1. Вероятность безотказной работы устройств обнаружения и коррекции ошибок в кодах ПСКВ с учетом обратного преобразования для поля Галуа GF(25)
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Калмыков И.А. Математические модели нейросете-вых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа/ Нейрокомпьютеры: разработка, применение. №8-9, 2003. С. 10-16.
- Калмыков И.А. Коррекция ошибок в модулярных кодах на основе нейросетевого алгоритма вычисления номера интервала/Зб1рник наукових праць Хар1вського ушверситету Повпряних Сил. Випуск 6(6). Харюв, 2005. с.65-68.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности/ Нейрокомпьютеры: разработка и применение, 2004, №5-6, с.94-101.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.



