В основу многих ИТ положена цифровая обработка сигналов, основу которой составляют ортогональные преобразования сигналов. Применение полиномиальной системы классов вычетов (ПСКВ) позволяет осуществлять такие преобразования в реальном масштабе времени [1]. Кроме того, параллельная обработка данных в вычислительных трактах мо модулям системы ПСКВ может служить базисом в реализации процедур поиска и коррекции ошибок. Разработанные алгоритмы обнаружения и исправления ошибок в нейросетевом базисе позволяют повысить эффективность ИТ систем управления.
Основу корректирующих кодов ПСКВ составляет распределение полиномов по полному диапазону. Если выбрать k из n оснований ПСКВ (kv) на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением
![]()
Многочлен A(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он принадлежит Ррaб(z). Второе подмножество, определяемое произведением r=n-k контрольных оснований,
![]()
задает совокупность запрещенных комбинаций. Вопросам разработки методов и алгоритмов контроля и коррекции ошибки в модульных избыточных кодах полиномиальной системы классов вычетов уделено значительное внимание [1,3]. Особое место отводится вычислению интервального номера полинома. Определения данной характеристики осуществляется
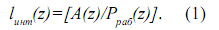
В работе [3] представлено устройство, осуществляющее обнаружение и коррекцию ошибки в модулярном коде на основе вычисления интервального номера, используя
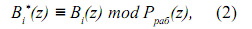
где B i*(z) и B i(z) - ортогональные базисы безизбыточной и полной системы. Тогда согласно (2)
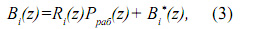
где 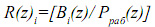
Подставив равенство (3) в выражение (1) и проведя упрощения, имеем
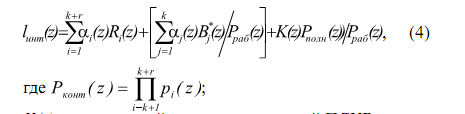
K(z) - ранг полной системы оснований ПСКВ. Так как множество значений интервального номера lинт(z) представляет собой кольцо по модулю p конт (z), то выражение (4) преобразуется к виду
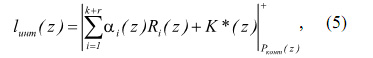
где ранг безизбыточной системы определяется выражением
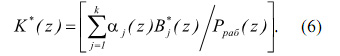
Если l инт (z)= 0, то исходный полином A(z) лежит внутри рабочего диапазона и не является запрещенным. В противном случае A(z) - ошибочная комбинация. Причем использование данной характеристики позволяет по величине lинт(z) определить местоположение и глубину Δa1(z) ошибки.
Анализ выражения (5) показывает, что применение составного модуля Р конт (z), по которому определяется значение интервального номера l(z), с точки зрения аппаратурных затрат, является не самым оптимальным.
Решить данную проблему можно за счёт модификации алгоритма [1]. В основу данной модификации положено свойство - отсутствие переноса единицы из младшего разряда в старший при выполнении арифметической операции сложения двух операндов в расширенных полях Галуа GF (2v). Таким образом, величина ранга K*(z) безизбыточной системы: ПСКВ p1(z),...,pk(z) определяется значением a 1(z) и B1*(z) , и никоим образом не зависит от переполнения диапазона ppaб(z). Следовательно, вычислив αiz можно отказаться от вычисления K*(z). Тогда (10) примет вид
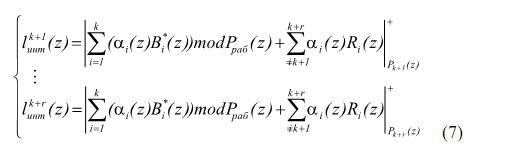
В ходе проведенных исследований было выявлено, что схемная реализация выражения (7) обеспечивает наибольшую эффективность при контроле и исправлении ошибок, возникающих в процессе функционирования спецпроцессора ПСКВ. При этом представленный алгоритм вычисления данной позиционной характеристики характеризуется довольно высокой надежностью работы при сравнительно небольших временных затратах на реализацию процедур поиска и определения местоположения ошибочных разрядов. Кроме того, с увеличением разрядности вычислительного устройства эффективность алгоритма (7) возрастает.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа/Нейрокомпьютеры: разработка, применение №8-9, 2003. С.10-16



