Применение систем контроля и управления доступом (СКУД) в современных системах управления позволяет обеспечить высокую степень защиты от несанкционированного доступа (НСД) к информации. При этом СКУД должны обладать свойством отказоустойчивости. Обеспечить высокую надежность работы таких систем можно за счет применения корректирующих арифметических кодов, используемых для первичной обработки биометрических параметров пользователя.
Решение
Биометрическая идентификация и аутентификация пользователя является одним из перспективных направлений защиты информации от НСД. В настоящее время наибольшее распространение получили системы контроля и управления доступом, базирующееся на статических параметрах пользователя. Однако данные системы слабо защищены от обмана муляжом. Данного недостатка лишены методы биометрической идентификации пользователя по его динамическим параметрам.
Однако для эффективной работы систем контроля управления доступом, использующих динамическую биометрию пользователя, необходимо осуществлять первичную обработку образа. Как правило, такая обработка основана на методах цифровой обработки сигналов (ЦОС). Известно, что большинство методов первичной обработки сигналов базируется на ортогональных преобразованиях, определенных в поле комплексных чисел, т.е. дискретном преобразовании Фурье, которое имеет ряд недостатков: низкая скорость обработки сигналов; аддитивные и мультипликативные погрешности из-за иррациональных значений поворачивающих коэффициентов Wkn. Кроме того, необходимо, чтобы возникающие ошибки при первичной обработки сигналов, были устранены в процессе этих вычислений.
Решить данные проблемы можно за счет применения специальной системы кодирования, которая бы поддерживала математическую модель ЦОС, обладающую свойством кольца или поля, а также была способна обнаруживать и корректировать ошибки. Данным требованиям удовлетворяет полиномиальная система классов вычетов (ПСКВ) [1-4]. Если в качестве оснований новой алгебраической системы выбрать минимальные многочлены p1(z) поля GF(pv), то любой сигнал x(n), представленный в полиномиальной форме X(z), удовлетворяющий условию
X(z) € P пол
где ![]() можно представить в виде П-мерного вектора
можно представить в виде П-мерного вектора
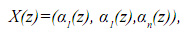
где 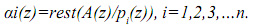
Наряду с повышением скорости обработки данных ПСКВ позволяет обнаруживать и корректировать ошибки, возникающие в процессе вычислений [2].
Полином, представленный в ПСКВ не содержит ошибки,если
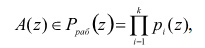
где k - количество информационных оснований ПСКВ (k < n)
Для обнаружения и коррекции ошибок в кодах ПСКВ используются позиционные характеристики, среди которых особое место занимают коэффициенты обобщенной полиадической системы (ОПС)[3]. Если полином, представленный ПСКВ, не содержит ошибок, то старшие коэффициенты ОПС, соответствующие контрольным основаниям равны 0, в противном случае - комбинация считается ошибочной.
Для эффективной реализации вычислений коэффициентов ОПС по значениям остатков ПСКВ был разработан алгоритм перевода из кода ПСКВ в код ОПС, который базируется на китайской теореме об остатках.
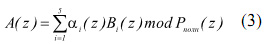
Представив ортогональные базисы в виде коэффициентов ОПС, получаем:
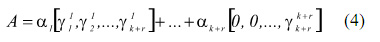
где у j i - коэффициенты ОПС j-го ортогонального базиса.
Тогда, проведя умножение вычетов αi. на соответствующие коэффициенты ОПС помодульно и поразрядно, при этом, учитывая превышение модуля pi как перенос единицы при суммировании результата, коэффициенты ОПС могут быть найдены
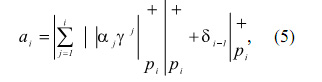
где δ i -l - переполнение, полученное при суммировании по модулю p i-l
Одним из важнейших свойств кодов ПСКВ, определенных в расширенных полях Галуа GF(pv), является отсутствие межразрядных переносов при вычислении результата по модулю p.(z). Это позволяет свести операцию итеративного получения коэффициентов ОПС к процедуре
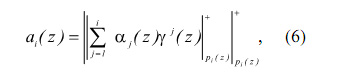
где i=1,2,...,n - количество оснований кода ПСКВ. Пусть задана ПСКВ со следующими полиномиальными основаниями:
рабочие p1(z)=z+1,p2(z) = z2+z+1,p3(z)=z4+z3+z2+z+1;
контрольные p4(z)=z4+z3+1;p5(z)=z4+z+1
При этом рабочий диапазон будет равен Pраб(Z)=z7+z6+z5+z2+z+1
В ОПС полином A(z) представляется в виде 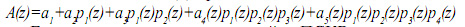
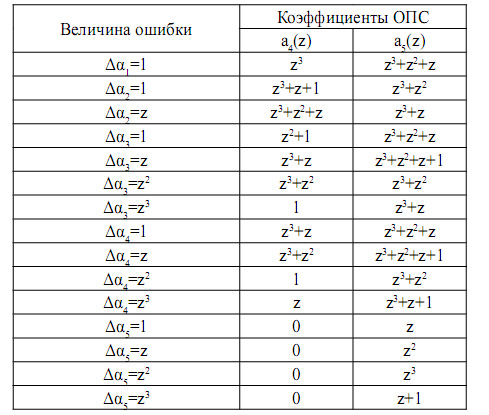
Если полином, представленный в ПСКВ, не содержит ошибок, то значения старших коэффициентов ОПС a4(z)=0, a5(z)=0. В табл. 1 представлена зависимость значений коэффициентов ОПС от местоположения и глубины ошибки.
Табл. 1.
На базе данного алгоритма был разработан преобразователь, который осуществляет параллельное вычисление коэффициентов смешанной системы счисления, реализованное с помощью нейроподобных вычислительных устройств. При этом характерной чертой патентованного устройства является то, что не только обнаруживает и корректирует ошибки, но и осуществляет обратное преобразование из непозиционного кода ПСКВ в позиционный двоичный код [3].
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
- Нейронная сеть для вычисления коэффициентов обобщенной полиадической системы, представленных в расширенных полях Галуа ОЕ(2у)Калмыков И.А., Лобо-дин М.В., Алексишин Е.В., Щелкунова Патент № 2258956.Бюл. №23 от 20.08.2005.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.



