В последнее время для анализа экономических систем используются методы биоэкономики. Биоэкономика - наука, объединяющая в себе методы эволюционной биологии, биологической антропологии и генетики.
В нашей работе для моделирования поведения совокупности адаптивных экономических агентов в паутинообразной модели использовался метод генетических алгоритмов [1]. Генетический алгоритм - стохастический метод глобального поиска, который реализует концепцию биологической эволюции. Генетические алгоритмы работают с популяцией возможных решений, применяя принцип «выживания наиболее приспособленных» для создания решений наиболее приближенных к цели. В каждом поколении создается новый набор индивидуумов при помощи их выбора и скрещивания путем применения операторов, заимствованных из генетики.
Паутинообразная модель описывает временное рыночное равновесие цен на отдельном рынке.
Пусть на конкурентном рынке существует n фирм, производящих одинаковый товар. Поведение каждой фирмы кодируется бинарной строкой длиной l. Эта строка кодирует действительное число, обозначающее количество продукции, которое решила произвести фирма i в цикле t.
Обозначим количество товаров, производимых фирмой i в цикле t через yi,t. Лица, принимающие в фирме решения, не знают цены следующего цикла в том момент, когда они определяют выпуск фирмы. Но им необходимо иметь ожидаемую цену 
. Исходя из этого ожидания, фирма i выбирает уровень выпуска, который принесет ей ожидаемой доход 
настолько большим, насколько это возможно. Оптимальное количество продукции для фирмы i задается через 
. Цена, определяющая рынок в цикле t, обозначается через pt и определяется с помощью обратной функции спроса. При рыночном равновесии ожидаемая цена должна в последствии совпадать с ценой равновесия, то есть 
для всех i, и все фирмы предпринимают одинаковые оптимальные действия 
для всех i и для некоторых 
.
Начальное состояние популяции задается случайным образом. Переход из цикла t в t+1 цикл осуществляется путем применения операторов генетического алгоритма [2]. Сначала необходимо представить стратегию каждой фирмы бинарной строкой. В работе количество выпускаемой продукции для k-ой фирмы определялось соотношением: 
, где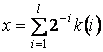 
, 
- значение i-го бита в строке k. Затем задавалась фитнес-функция, реализующая принцип выживания сильнейшего. В качестве фитнес-функции бралась функция дохода:
,
где 
означает цену, при условии, что вся популяция находится в состоянии 
.
Далее при помощи оператора пропорционального отбора выбирались фирмы, чьи значения функции приспособленности были большими. Тогда стратегии, дававшие среднюю прибыль, будут в дальнейшем в среднем использованы большим количеством агентов. Выбранные строки на следующем этапе разбиваются напополам, и к каждой паре с заданной вероятностью применяется оператор одноточечного кроссовера. После применения кроссовера каждый бит в каждой строке меняется на противоположный с заданной мутационной вероятностью.
Для моделирования была написана программа в пакете MATLAB при помощи инструментальной панели GA Toolbox. В данной инструментальной панели используются матричные функции пакета MATLAB для создания набора универсальных инструментов, обеспечивающих применение широкого диапазона методов генетических алгоритмов.
В результате проведения ряда экспериментов было обнаружено, что при любом задании параметров паутинообразной модели наблюдается резкое приближение к равновесному уровню. То есть фирмы способны были изменять свои решения таким образом, что количество выпускаемой ими продукции оставалось оптимальным, после довольно короткого периода эволюции.
В классической паутинообразной модели [3] возможна ситуация, когда на рынке не существует равновесия. Это происходит тогда, когда абсолютный наклон линии спроса превышает наклон линии предложения. Вместе с тем, эволюционное моделирование паутинообразной модели, проведенное в пакете MATLAB, демонстрирует, что процесс эволюции всегда сходится к некоторому равновесному состоянию вне зависимости от абсолютных наклонов линий спроса и предложения. Можно показать, что теорема шим (Schema theorem) объясняет данный феномен.
СПИСОК ЛИТЕРАТУРЫ
- J. Holland, Adaptation in Natural and Artificial Systems, University of Michigan Press: Ann Arbor, USA, 1975.
- Herbert Dawid, Michael Kopel. On economic applications of the genetic algorithm: a model of the cobweb type. // Journal of Evolutionary Economics (1998), 8: 297-315.
- Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. Электронный учебник.