Допустим мы имеем некоторую рыночную ситуацию в идеальном рынке. Для того чтобы найти наиболее вероятную таблицу расклада [4] предлагаю воспользоваться следующей логикой
У i-го предложения существует ниша, которую оно готово предоставить под j-ый спрос. У j-го спроса существует ниша, которая может реализоваться за счет i-го спроса. Это разные величины, однако практические 
= min(
).
Тогда для n-го уровня спроса и первого уровня предложения получаем:
,
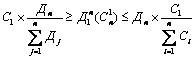а значит
Поскольку на различных этапах расчета какого-то одного Дj (
)(верхний индекс - ценовой уровень спроса, нижний - ценовой уровень предложения, нишу в котором занимает данный спрос; у предложения наоборот) возможно использование различных частей формулы, то необходимо в последующих расчетах учитывать результаты предыдущих, устраняя их из расчетов. В противном случае смена формулы расчета min приведет к эффекту расчета по этой формуле всех предыдущих вариантов, а, значит, автоматически приведет к ошибке.
Поэтому для 
имеем
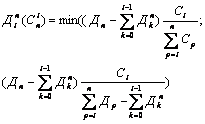
Напомним, что нулевого уровня спроса, как и предложения не существует.
Расчет по этой формуле возможен для всех уровней, если после каждого расчета удалять n-ый уровень спроса и предложения, а из всех уровней предложения (от 1 до n-1) вычесть 
. В итоге уровень n-1 станет уровнем n´.
Однако этот «окольный» вариант можно было бы получить лишь в случае разработки формул для более высокого уровня, поскольку они имеют ряд особенностей. Именно их разработка позволила впоследствии получить приведенную формулу для уровня n.
Для уровня n-1 формула будет иметь вид:
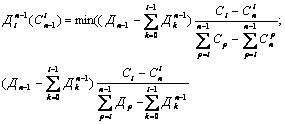
Соответственно для того, чтобы рассчитывать спрос для уровня n-1 нужно рассчитать спрос (и само собой разумеется предложение) для уровня n.
Соответственно для того, чтобы рассчитать спрос для j-го уровня требуется расчет спроса для уровней n ... j+1.
Для 
, где j ≥ i имеем формулу вида
Соответственно, использование данной формулы для ситуации с пятью ценовыми уровнями спроса и предложения (столбец Дj и строка Сi из табл. 1) выделило следующую наиболее вероятную таблицу расклада (представлены только сделки), которая размещена в строках и столбцах 1-5 в таблице 1.
Таблица 1. Результаты расчетов
|
|
|
||||||||
|
|
j i |
1 |
2 |
3 |
4 |
5 |
Дj |
ДΣ |
Достаточное |
|
1 |
3 |
- |
- |
- |
- |
40 |
3 |
37 |
|
|
2 |
2 |
8 |
- |
- |
- |
35 |
10 |
25 |
|
|
3 |
2 |
6 |
21 |
- |
- |
30 |
29 |
1 |
|
|
4 |
2 |
4 |
7 |
9 |
- |
22 |
22 |
- |
|
|
5 |
1 |
2 |
4 |
5 |
6 |
18 |
18 |
- |
|
|
Сi |
10 |
20 |
32 |
38 |
49 |
|
|
|
|
|
CΣ |
10 |
20 |
32 |
14 |
6 |
|
|
|
|
|
Cостаточное |
- |
- |
- |
24 |
43 |
|
|
|
|
СПИСОК ЛИТЕРАТУРЫ
- Вентцель Е.С. Теория вероятностей. // М.: Высшая школа, 2002
- Гмурман В.М. Теория вероятностей. Учебник для ВУЗов.// М.: Высшая школа, 2003
- Евтодиева Т.Е. Логистические основы процесса сбытовой деятельности// Самара, СГЭА, 2000
- Клёнов М.В., Ольшанский А.М. Моделирование сбыта продукции предприятия // Самара, 2004