В работах [1, 2] известный метод Римана для гиперболического уравнения второго порядка распространен на одномерные гиперболические системы общего вида. Получено явное представление решений задачи Коши. Ядрами интегральной формулы служат матрицы двух типов, получившие название матриц Римана первого и второго рода и представляющие собой сингулярную и регулярную компоненты фундаментальной матрицы гиперболической системы. Изучена детальная структура матриц Римана. В [3 - 5] этот математический аппарат применен к анализу асимптотического поведения решений задачи Коши. В частности, в [4] построен оператор монодромии системы указанного в названии класса, получены спектральные признаки устойчивости и дихотомии; в пространственно-однородном случае вычислена резольвента оператора монодромии, получено конструктивное описание его спектра.
В [6, 7] предложен подход к анализу устойчивости решений краевых задач для одномерной гиперболической системы на основе прямого метода Ляпунова: в [6] - для задачи Коши, в [7] - для смешанной задачи, встречающейся в акустике, химической кинетике. В [7] получено приложение к анализу устойчивости стационарных режимов в химических реакторах.
Данный доклад - продолжение [6, 7]. Рассматривается, как и в [4], задача Коши для системы указанного в названии класса. Построен вариант прямого метода Ляпунова, в котором условие на производную функционала Ляпунова вдоль траекторий системы существенно ослаблено по сравнению с общей ситуацией в [6].
Рассмотрим гладкий гиперболический оператор с кратными характеристиками
.
Здесь
- единичная матрица порядка 
. Будем предполагать
1) A, B периодичны по t с периодом T>0;
2) 
ограничены в 
.
Обозначим H линеал гладких финитных функций 
.
Задача Коши
(1)
однозначно разрешима в классе гладких функций 
и при каждом 
. Введем в H скалярное произведение и норму формулами 
. Зафиксируем гладкую ограниченную вместе с производными первого порядка матрицу 
порядка N со свойствами
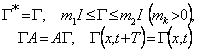(2)
и определим функционал 
равенством
.
Производная функционала вдоль траекторий системы (1) дается формулой
.
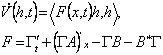ТЕОРЕМА. Пусть существует матрица 
со свойствами (2) такая, что
1º) 
в полуплоскости 
;
2º) 
хотя бы на одной прямой 
.
Тогда решение 
системы (1) экспоненциально устойчиво: существуют постоянные 
такие, что для любого решения
. (3)
ДОКАЗАТЕЛЬСТВО. Обозначим 
разрешающий оператор задачи Коши (1). Из формулы для решения задачи Коши в [1] следует: - линейный ограниченный (при фиксированных 
) оператор 
, гладкий по в операторной топологии, при этом выполняется равенство (свойство стационарности на периоде)
(4)
1. Пусть условия 1º, 2º выполняются при 
. Имеем для значений 
на любом решении u(x,t) равенства
.
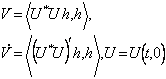Условия 1º, 2º дают:
(5)
при некотором t≥0.
Из второго неравенства (5) легко получить: существует t0>0 такое, что
(6)
Зафиксируем период 
; с учетом (6) и первого неравенства (5) имеем: число
(7)
Далее, из (4) вытекает равенство
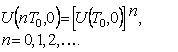(8)
Из (7), (8) с учетом априорной оценки для решения задачи Коши (1) вытекает для решений (1) оценка (3) с константой 
.
2. В общем случае замена Ляпунова 
где 
- эрмитово-положительный корень из 
, приводит к ситуации пункта 1.
Заметим, что требования 1º, 2º на 
существенно слабее, чем в аналогичной ситуации в [6] для систем с любыми гладкими коэффициентами.
СПИСОК ЛИТЕРАТУРЫ
- Романовский Р.К. О матрицах Римана первого и второго рода// Докл. АН СССР 1982. Т. 267, №3. С. 577 - 580.
- Романовский Р.К. О матрицах Римана первого и второго рода// Мат. сб. 1985. Т. 127, №4. С. 494 - 501.
- Романовский Р.К. Экспоненциально расщепляемые гиперболические системы с двумя независимыми переменными// Мат. сб. 1987. Т. 133, №3. С. 341 - 355.
- Романовский Р.К. Об операторе монодромии гиперболической системы с периодическими коэффициентами// В книге: Применение методов функционального анализа к задачам математической физики. Киев: Изд. ИМ АН УССР 1987. С. 47 - 52.
- Романовский Р.К. Усреднение гиперболических уравнений// Докл. АН СССР 1989. Т. 306, №2. С. 286 - 289.
- Воробьева Е.В., Романовский Р.К. Об устойчивости решений задачи Коши для гиперболической системы с двумя независимыми переменными// Сиб. мат. журн. 1998. Т. 39, №6. С. 1290 - 1292.
- Романовский Р.К., Воробьева Е.В., И.Д. Макарова. Об устойчивости решений смешанной задачи для почти линейной гиперболической системы на плоскости// Сиб. журн. индустриальной математики 2003. Т. VI, №1. С. 118 - 124.