Для оценки динамических процессов, происходящих при криволинейном движении лесовозного автопоезда (ЛАП-а), необходимо знать кинематические параметры его основных элементов и характерных точек и связь между ними.
В реальных условиях движение ЛАП-а по кривым характеризуется явно выраженной кинематической нестационарностью. Поэтому в основе его изучения должны лежать комплексные исследования дважды (геометрически и кинематически) нестационарных режимов, которые представляют собой наиболее распространенный вид движения и качественно отличаются от стационарных.
В проекции на опорную поверхность движение каждого элемента ЛАП-а в приближении можно считать плоско-параллельным.
Задачами исследований является определение траекторий характерных точек автопоезда, линейных и угловых скоростей и ускорений, построение подвижной и неподвижной центроид, кругов Лагира и Брессе, свидетельствующих о знакопеременности нормальных и касательных ускорений [1].
Разработанная математическая модель [2] позволяет решать геометрические задачи криволинейного движения ЛАП-а в условиях голономных связей без учета параметра времени, в результате чего можно получить соотношения между кинематическими параметрами.
При заданном законе движения вдоль основной траектории s=s(t) [3] скорость, касательное и нормальное ускорения средней точки задней оси автомобиля
, 
, 
,
где ρ - радиус кривизны.
Исходя из теории плоского движения определяются кинематические параметры характерных точек и основных элементов ЛАП-а [2]. При этом линейные и угловые скорости связаны между собой аналогичными соотношениями, что линейные и угловые перемещения, соответственно.
Скорость и ускорение произвольной точки М
, 
,
где 
- скорость и ускорение точки Ai, выбранной за полюс.
Угловая скорость и угловое ускорение i-того элемента автопоезда
, 
,
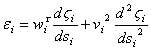где 
- угол поворота i-того элемента ЛАП-а, 
- скорость и перемещение точек продольной оси элемента вдоль нее.
Касательные ускорения центров масс элементов ЛАП-а имеют место как при неравномерном движении из-за проявления кинематической нестационарности, так и при равномерном, когда сказывается геометрическая нестационарность.
Уравнение неподвижной центроиды i-того элемента
, 
,
где 
- координаты полюса Ai в неподвижной системе координат.
Соответственно, уравнение подвижной центроиды
,
,
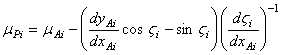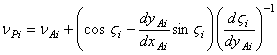где 
- координаты полюса Ai в подвижной системе координат.
Окружность
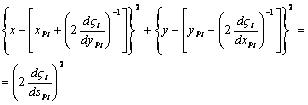
представляет собой геометрическое место точек, нормальные ускорения которых равны нулю (точек перегибов траекторий). Ограниченный ею круг является кругом Лагира (поворотным кругом).
Окружность
,
где 
, определяет семейство точек, для которых отношение 
является постоянной величиной. С введением параметра времени касательные ускорения этих точек равны нулю. Образованная ими окружность ограничивает круг Брессе (круг перемены).
Полученные кинематические соотношения в дальнейшем могут быть положены в основу динамических исследований движения ЛАП-а по кривым. Они позволяют провести многосторонний анализ изучаемых процессов при различных законах - разгоне, равномерном движении, торможении.
СПИСОК ЛИТЕРАТУРЫ
- Соколов, Г. М. Исследование точек подвижной плоскости по геометрическим признакам / Г. М. Соколов. - ВИНИТИ, 1985. № 3309-85. - 34 с.
- Соколов, Г. М. Движение лесовозного автопоезда на кривых. Теория. Расчет. Эксперимент / Г. М. Соколов. - ВИНИТИ, 1998. № 2507-В98. - 274 с.
- Закин, Я. Х. Прикладная теория движения автопоезда / Я. Х. Закин. - М.: Транспорт, 1967. - 356 с.