Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Ранее были получены уравнения для расчета коэффициентов растворимости σ и диффузии D для непористых полимерных мембран в рамках фрактальной модели процессов газопереноса:

,               (1)

,            (2)

где  и  - константы,  и  - эффективные площадь поперечного сечения и диаметр молекулы газа-пенетранта, соответственно, D_f - размерность областей локализации избыточной энергии, (ε/k)_эф - эффективная силовая постоянная потенциала Ленарда-Джонса, рассчитанная для взаимодействий газ-газ, f_c - относительный флуктуационный свободный объем полимера, d_h - диаметр микрополости этого объема, D_n - размерность структуры полимера, контролирующая процессы газопереноса, в качестве которой может выступить либо D_f, либо фрактальная размерность структуры полимера d_f, d_s - спектральная размерность структуры полимера.

Коэффициент газопроницаемости полимера Р может быть выражен следующей простой формулой:

,           (3)

а коэффициент селективности двух газов i и k α_ik на полимерной мембране определяется так:

.              (4)

Сочетание уравнений (1)-(4) позволяет получить следующее общее соотношение для определения a_ik в рамках фрактальной модели:

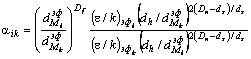,         (5)

где показатели в последнем множителе правой части уравнения (5) записаны в таком виде потому, что в общем случае для одной и той же полимерной мембраны величины D_n могут быть разными для различных газов i и k в зависимости от величины .

Цель настоящего сообщения - показать принципиальную применимость уравнения (5) для прогнозирования величины a_ik (селективности мембраны) на примере 4 полимеров и серии углеводородов С₁-С₄.

Использованы литературные данные для четырех полимеров: аморфно-кристаллического полиэтилена (ПЭ) со степенью кристалличности 0,57, стеклообразного аморфного поливинилтриметилсилана (ПВТМС) и сшитых каучуков полиизопрена (ПИ) и полидиметилсилоксана (ПДМС). Величины a_ik получены для них как отношение P_i/P_k, где в качестве P_k использована величина Р для метана (СН₄), а в качестве Р_i - величины Р для 11 остальных углеводородов С₁-С₄. Величины  и (ε/k)_эф взяты из литературных источников. Значения d_f приняты равными: 2,77 для ПЭ, 2,83 для ПВТМС и 2,90 для ПИ и ПДМС. Величина d_s для линейных ПЭ и ПВТМС принята равной 1,0, а для сшитых ПИ и ПДМС - равной 1,33.

Ранее было показано, что процессы переноса углеводородов в рассматриваемых полимерах нужно исследовать в рамках мультифрактального формализма, т.е., размерность D_f не является постоянной, как в случае монофрактального представления, а зависит от масштаба измерения (в данном случае ). Было получено следующее соотношение между D_f и (ε/k)_эф:

.                   (6)

Полученный таким образом спектр D_f( ) был принят одинаковым для всех четырех полимеров, что, конечно же, является аппроксимацией. Далее, также для всех четырех полимеров было принято D_n=d_f.

В таблице 1 приведено сравнение величин коэффициента селективности углеводородов a_ik по метану, рассчитанных по уравнению (5)  и полученных из литературных источников . Как можно видеть, для всех четырех полимеров получено достаточно хорошее соответствие (среднее расхождение между  и  для 44 пар составляет 20 %).

Таблица 1. Размерности D_f, сравнение  и литературных  величин коэффициента селективности и их расхождение Δ для 11 углеводородов С₁-С₄ на примере ПЭ, ПИ, ПДМС и ПВТМС.

Этот результат позволяет сделать следующие выводы.

1) Предложенная фрактальная модель процессов газопереноса для непористых полимерных мембран является перспективной для компьютерного прогнозирования и моделирования указанных процессов.

2) Очевидно, что для повышения точности результатов модели существует несколько способов, изложенных в последующих пунктах.

3) Как следует из данных таблицы 1, спектры D_f( ) близки, но не одинаковы для рассматриваемых полимеров, что видно по разной погрешности для одного и того же газа, но разных полимеров. Таким образом, требуется точная идентификация спектра D_f( ) для каждого полимера.

4) Имеющиеся в литературе величины (ε/k) и d_M могут иметь достаточно широкий разброс (для одного и того же газа они могут различаться в 1,5-2,0 раза). Поэтому важно иметь более точные методы оценки эффективных величин этих параметров.

5) Указанная точность необходима, поскольку характерной особенностью всех скейлинговых и фрактальных соотношений является степенная зависимость, существенно повышающая погрешность расчета.

6) Степень связности структуры полимера, характеризуемая величиной d_s, существенно влияет на величину α_ik. Так, увеличение d_s от 1,0 для линейных полимеров до 1,33 для сшитых при прочих равных условиях увеличивает α_ik в среднем в 1,5 раза. Поэтому следует использовать точную величину этой размерности.