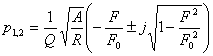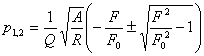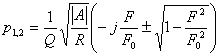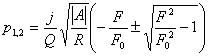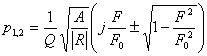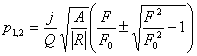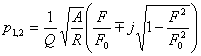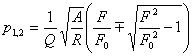Еще Р.Кеттелом, а чуть позднее Г.Айзенком было показано [5], что реакцию человека на некоторую стимулирующую ситуацию можно описать функцией или моделью
K = f ( S, P ),
где P - характеристики личности человека, S - характеристики стимулирующей ситуации, K - ответная реакция. Конкретное выражение этой модели можно получить различными способами, в частности, экспериментально или путем рассуждений по аналогии. Попробуем отыскать его с помощью аналогии, полагая, что S - информационное воздействие. Убедительным обоснованием правомерности ее использования в таком случае служит работа Л.Куффиньяля [3], в которой он аргументировано демонстрирует сходство динамики психической реакции человека на информационное воздействие с процессом, протекающим в электрической цепи под воздействием импульса напряжения. Поскольку между электрическими процессами и процессами, происходящими в оптических, гидравлических, механических и других физических системах, также есть существенное сходство, то, следуя Куффиньялю, очевидно, можно говорить об аналогии и между психической реакцией и неэлектрическим процессом.
Пусть, далее, имеется механическая система. Если на эту систему воздействует некоторая сила X, то система приходит в движение, начинает перемещаться. При этом возникают различного рода потери, и величина перемещения Y оказывается связанной с величиной X дифференциальным уравнением динамики
![]()
где m - инерционная масса системы, r - коэффициент вязкого трения, c - жесткость, обусловленная упругими свойствами системы.
Нетрудно заметить, что если силу X интерпретировать как силу информационного воздействия, имеющую смысл S, а Y - как уровень реакции человека, имеющий смысл K, то m, r и c можно рассматривать как величины, аналогичные таким характеристикам P личности человека, как ригидность, фрустрированность и агрессивность. Действительно, ригидность - это свойство, характеризующее психологическую инерционность, негибкость; фрустрированность - состояние, возникающее, когда на пути к достижению цели встречаются непреодолимые препятствия, и проявляющееся в отчаянии, депрессии, отказе от активной деятельности и пр.; агрессивность - повышенная склонность к противодействию, отторжению, стремление энергично возражать по каждому поводу и т.п. Таким образом, уравнение динамики механической системы описывает процесс, аналогичный психической реакции человека, и из него, вероятно, можно получить динамическую модель реакции, являющуюся реализацией функции K.
Воспользуемся для получения модели теорией размерностей. Интерпретируем массу m в уравнении динамики механической системы, измеряемую в кг, как ригидность R, измеряемую в некоторых условных баллах, и представим перемещение Y, измеряемое, допустим, в метрах, как уровень реакции, измеряемый в условных единицах, которые, например, в честь Г. Айзенка, назовем гай. Тогда первый и остальные члены уравнения динамики механической системы приобретут размерность балл × гай /сек2 (назовем ее в честь Р.Кеттела кет), что является интерпретацией размерности механической силы, выраженной в ньютонах ( 1 н = 1 кг× м /сек2 ), и имеет смысл размерности X как силы информационного воздействия. Величина r при этом получит размерность балл × сек взамен н × сек/м или кг/сек, а величина с - размерность балл/сек2 взамен н/м или кг/сек2.
Используем далее результаты интерпретации, полагая, что наличие сек в размерности обусловлено существованием некоторого временного параметра Q, и составим на основе уравнения механической системы «черновую» модель психической реакции
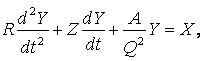
где A - агрессивность человека, выраженная в баллах, а Z - пока неизвестный коэффициент, зависящий от фрустрированности F . Если теперь в этой «черновой» модели определить Z, то получим «чистовую», окончательную модель, которая нас интересует.
Коэффициент при Y не зависит ни от R, ни от F, а потому определен непосредственно из размерности ( балл/сек2). Что касается коэффициента Z , то таким же образом его определить нельзя. Причина в том, что психологическая реакция - процесс колебательный. Это известно из инженерной психологии [2], в которой человек исследуется как звено системы управления. В теории управления [1] колебательное звено обычно описывается уравнением динамики
T2 ![]() ,
,
где T - постоянная времени, ξ - коэффициент затухания колебаний, k - коэффициент усиления. И поскольку T входит в коэфффициенты при первом и втором членах уравнения, величина Z непосредственно через размерность не определяется. Чтобы ее найти, разделим обе части уравнения на k
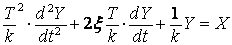
и сопоставим полученное с "черновой" моделью. Из сопоставления становится ясно, что T2 / k эквивалентно R , 1 / k эквивалентно A/Q2 , а Z эквивалентно 2 ξ T/ k.
Вычислив T/ k через R и A/Q2 , получим
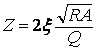 .
.
Выражая F подобно R и A в баллах, коэффициент затухания, исходя из его физического смысла, можно представлять как
![]() ,
,
где F0 - некоторое значение уровня фрустрированности, считающееся нормальным или пороговым ( при определении фрустрированности, например, по методике, описанной в [6], F0 = 10). Подставив последнее выражение для коэффициента ξ в формулу для Z, а затем Z в «черновую» модель, получим «чистовую» модель
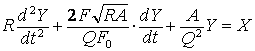 .
.
Это и есть искомая модель в окончательном виде. Исследуем её методами теории автоматического управления [4], для чего представим её в операторной форме и запишем характеристическое уравнение отображаемого ею процесса в виде
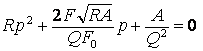 .
.
Решая это уравнение, найдем его корни
 .
.
Исследуем их, полагая, что F - величина однонаправленная (F ≥ 0), а R и A - двунаправленные (ригидности соответствует её альтернатива пластичность, а агрессивности - терпимость), что предопределяет возможность R>0, R<0 и A>0, A<0.
В общем случае корни характеристического уравнения - комплексные числа, содержащие действительную и мнимую части. Известно [4], что если действительные части этих чисел отрицательные, то процесс устойчив. Если среди них есть хотя бы одна положительная - то неустойчив. Если они равны нулю, то процесс находится на грани устойчивости. Подставляя в связи с этим в формулу для корней положительные и отрицательные R, отвечающие соответственно ригидности и пластичности, и положительные и отрицательные А, отвечающие соответственно агрессивности и терпимости, а также различные значения F, получим результаты, приведенные в таблице.
Таблица 1. Влияние параметров модели на характер психической реакции
|
A |
R |
F |
Вид корней характеристического уравнения в аналитической форме |
Расположение корней на комплексной плоскости*) |
Вид процесса (психической реакции) |
|
>0 |
>0 |
<F0 |
|
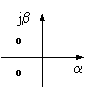 |
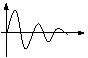
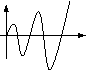
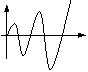
устойчивый колебательный
|
|
>0 |
>0 |
>F0 |
|
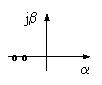 |
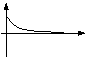
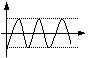
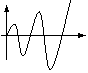
устойчивый апериодический
|
|
<0 |
>0 |
<F0 |
|
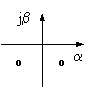 |
неустойчивый
|
|
<0 |
>0 |
>F0 |
|
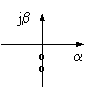 |
на грани устойчивости
|
|
>0 |
<0 |
<F0 |
|
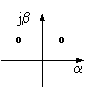 |
неустойчивый
|
|
>0 |
<0 |
>F0 |
|
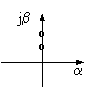 |
на грани устойчивости
|
Продолжение таблицы 1. Влияние параметров модели на характер психической реакции
|
A |
R |
F |
Вид корней характеристи-ческого уравнения в аналитической форме |
Расположение корней на комплексной плоскости*) |
Вид процесса (психической реакции) |
|
<0 |
<0 |
<F0 |
|
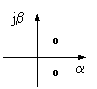 |
неустойчивый
|
|
<0 |
<0 |
>F0 |
|
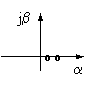 |
неустойчивый
|
|
>0 |
>0 |
=0 |
|
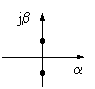 |
на грани устойчивости
|
|
<0 |
<0 |
=0 |
|
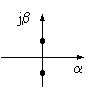 |
на грани устойчивости
|
|
=0 |
≠ 0 |
≥ 0 |
|
 |
неустойчивый
|
|
≠ 0 |
=0 |
>0 |
корней нет |
- |
повторяет внешнее воздействие |
*) α - ось действительных чисел, jβ - ось мнимых чисел.
Из таблицы видно, что устойчивая психическая реакция свойственна лишь людям, обладающим определенными ригидностью и агрессивностью и некоторой фрустрированностью. Людям, обладающим пластичностью и терпимостью, а также нулевой фрустрированностью свойственна неустойчивая реакция, либо реакция, находящаяся на грани устойчивости. Это вполне объяснимо: люди «пластичные» обладают повышенной «податливостью» влияниям внешних воздействий, а люди с высоким уровнем терпимости не способны отторгать негативные воздействия на них. Те и другие и «откликаются» на указанные воздействия активными внутренними переживаниями, а иногда и стрессами. Интересно отметить, что агрессивность и ригидность существенно влияют на продолжительность реакции. Чем больше ригидность и меньше агрессивность, тем дольше длится реакция. Рост фрустрированности приводит к сокращению длительности реакции и к некоторому сглаживанию её, уменьшению максимумов при колебаниях.
Предложенная модель и результаты её исследования, несомненно, могут вызвать возражения. Главное из них очевидно: психологический портрет личности не ограничивается описанием ригидности, фрустрированности и агрессивности, а потому реакция на информационное воздействие будет зависеть не только от них. Не отрицая этого полностью, с этим, все же, можно поспорить, поскольку общепризнанно, что перечисленные характеристики личности - основные. Подавляющее же большинство остальных характеристик так или иначе можно выразить через них. Так, например, тревожность, в зависимости от того, насколько человек невротичен, в какой степени он экстраверт или интроверт, может быть характеристикой либо вообще несущественной, либо «генерирующей» определенные ригидность и агрессивность [5]. Возможны и иные возражения, однако в ответ на них следует отметить, что авторы работы не претендуют на ее исключительность, отвергающую другие подходы к изучению психической реакции. Описанное - лишь метод и данные, дополняющие уже известное.
СПИСОК ЛИТЕРАТУРЫ
- Голубничий Н., Зайцев Г., Иващенко М., Чинаев П. Беседы по автоматике. Киев: Техника, 1971, 232 с.
- Котик М. Курс инженерной психологии. Таллин: Валгус, 1978, 364с.
- Куффиньяль Л. Кибернетика - искусство управления //Кибернетика ожидаемая и кибернетика неожиданная. М.: Наука, 1968. С. 122-142.
- Лотош М. Теория автоматического управления. М.: Наука, 1979, 256 с.
- Хьелл Л., Зиглер Д. Теории личности. СПб.: Питер, 1997, 608 с.
- Шпалинский В., Морозов Л. Введение в современную теорию личности и коллектива. Харьков: Гуманитарная академия, 1995, 134 с.