В процессе автоматизации и объективизации скрининговых операций возникает задача построения адекватных решающих правил по соотнесению исследуемого пациента к определенному классу заболеваний по результатам базовых лабораторных исследований (например, общему анализу крови). В связи с этим, базируясь на клинический опыт теоретической и экспериментальной медицины школы Завьялова А.В. и собственные исследования, предлагается следующая технология построения диагностических решающих правил.
На первом этапе осуществляется сбор фактологического репрезентативного материала и отбрасываются артефакты. Общая выборка случайным образом делится на три части - обучающую, настраивающую и экзаменационную. На перовой рассчитываются показатели системной организации (см. далее), на второй определяются функции принадлежности, на третьей подвыборке определяется эффективность идентифицированных диагностических решающих правил. Соотношения статистических мощностей указанных подвыборок рекомендуется выбирать исходя из взаимной репрезентативности (они должны подчиняться подобным законам распределения). Опыт доказывает, что этого можно достичь, используя случайную сортировку (равномерный закон распределения) и принцип «золотого сечения», т.е. примерное соотношение объемов указанных подвыборок - 0,46:0,32:0,22.
На втором этапе на обучающей выборке синтез диагностических матриц предлагается осуществлять по следующей методике.
Допустим нам необходимо осуществить диагностику К классов. (В медицине - один из классов - базовый - это здоровые люди.) В общем случае формируется матрица признакового пространства Х. Для каждого признака j в классе k определяем закон распределения (при маломощности подвыборок рекомендуется в данном случае использовать метод Уразбахтина И.Г. - «приведенные распределения») и ему соответствующую медиану Мjk и среднеквадратичное отклонение от нее 
. Для классов k и l определяются матрицы парной корреляции, соответственно, состоящие из элементов 
и 
(под элементами здесь понимаются значения корреляционного отношения в классе l между признаками i и j, превышающие выбранный уровень статистической значимости; если рассчитанное значение меньше порога, то ему соответствующее значение элемента матрицы принимается равным 0). Тогда некоторая «точка-пациент» 
- классу характеризуется следующим показателем отклонения (назовем его показателем системной организации) от «центра масс» медиан класса l PRml, определяемым по формуле 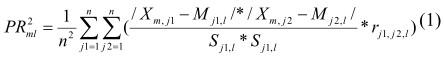(1).
(1)
где n- количество регистрируемых признаков.
Если есть возможность оценки информативности признаков (индивидуальной и совместной), например, с помощью экспертного анализа, анализа функций распределения или методом максимального правдоподобия, 
, то каждое слагаемое в формуле (1) необходимо умножить на данный коэффициент информативности.
После проведения описанной процедуры получаем для каждого класса вектор квадратов значений PRml , который характеризуется значением медианы МPRml. Изменяя k и l по всему множеству классов, получаем матрицу МPRК,К (К - количество классов).
Третий этап проводится, используя настраивающую выборку. Для каждого объекта z из нее по формуле (1) определяются показатели системной организации и формируется матрица ZPR, состоящая из элементов - квадратов значений PRz,l,k. Затем, для каждой точки z определяется матрица относительных отклонений от матрицы МPR - DPR:
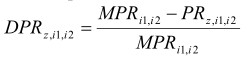(2)
i1,i2=1,K -номера диагностируемых классов.
Обрабатывая следующим образом z матриц, формируем матрицу функций принадлежностей μ на носителях DPR. Определяются законы распределения Fi1,i2(DPRi1,i2) и, задавшись необходимыми точностью и уровнем статистической значимости, строятся классификационные интервалы ΔDPRi1,i2: ΔDPRi1,i2=Mi1,i2(DPRi1,i2)±γi1,i2·σi1,i2(DPRi1,i2), где Мi1,i2(), σi1,i2() - операторы вычисления моды и СКО(DPRz,i1,i2) в классах i1 и i2, соответственно, γi1,i2- множитель, определяющий размер классификационного интервала (вычисляется, исходя из анализа пересечений функций Fi1,i2(DPRi1,i2), Fi1,i1(DPRi1,i1), Fi2,i2(DPRi2,i2) Fi2,i1(DPRi2,i1) ).
Функции принадлежности определяются как: μi1,i2=Fi1,i2(DPRi1,i2)*(1-βi1,i2), если у обследуемого DPRi1,i2 ∉ ΔDPRi1,i2, и μi1,i2 = (1-βi1,i2), в противном случае. (βi1,i2 - ошибки второго рода применения решающих правил для элементов матрицы (i1,i2), определенные на настраивающей выборке).
На экзаменационной выборке рассчитываются коэффициенты согласия каппа между истинным диагнозом (здесь возможно так же применение мнения экспертов) и результатами диагностике по полученным матрицам MPR, DPR и μ. В случае хорошего результата, указанные матрицы используются в соответствующей автоматизированной системе скрининг диагностики.
При принятии решения для конкретного пациента применяется формулы (1) и (2) и определяется матрица классификационных значений функций принадлежностей μb по μ. Пользователю сообщается указанная матрица функций принадлежностей с указанием (выделением) L (L-свобода выбора решений) наиболее вероятных ситуаций и вектор коэффициентов уверенности соотнесения состояния пациента к определенному классу. К ним относятся ситуации с максимальными значениями функций принадлежностей и непротиворечивые между собой (определяются по анализу над и поддиагональных элементов). В качестве коэффициентов уверенностей рассматриваются значения функций принадлежности. Решающее правило о принадлежности состояния исследуемого к классу k формируется в виде заключения типа: «по результатам исследования пациент относится к классу (заболеванию) k с уверенностью UK» (k=1,...K).
Уверенность принадлежности к классу k UK рассчитывается следующим образом. Выделяются все значения функций принадлежности k-ой строки и k-го столбца, превышающий определенный пороговый уровень - пусть всего таких значений будет Т. Затем, применяется итерационная формула:
(3)
UK0=0, t=1,2...T.
Теоретические исследования автора показали, что вместо (3) оптимальнее применять формулу (4), обладающей большей чувствительностью, для которой (3) является частным случаем обладающим плохим асимптотическим свойством по мере приближения к единичному значению.
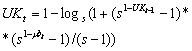, (4)
где 
.
Заметим, что если к матрице функций уверенностей μ применить процедуры агрегатирования (например, перемещение ее элементов таким образом, чтобы вокруг главной диагонали выстраивались элементы с максимальными значениями), то анализ вновь полученной матрицы позволяет выстроить иерархию классов в пространстве состояний.
Формулу (4) применима так же для вычисления коэффициента уверенности наличия у пациента или заболевания А1 или заболевания А2 или заболевания А3 и т.д. В случае необходимости расчета коэффициента уверенности наличия у пациента заболевания А1 и заболевания А2 и заболевания А3 и т.д. рекомендуется применять формулу 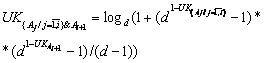(5).
, (5)
где 
.
В общем случае, необходимо учитывать коэффициенты неуверенности. Они могут быть построены аналогичным образом, построив матрицу функций непринадлежности.
Для описанной технологии синтеза и применения диагностической матрицы создано соответствующее программное обеспечение.