В самых общих терминах, метаданные - это данные о данных. Более точное определение: метаданные - это структурированные данные, описывающие характеристики информационных объектов (в частности, ресурсов Веба) и имеющие целью способствовать их поиску, идентификации и оценке, а также управлению этими объектами.
Метаданные играют ключевую роль в Семантическом вебе. С их помощью выполняется семантическая аннотация веб-ресурсов. Метаданные передают (частично) семантику ресурсов. Другими словами, метаданные, выполняющие семантическую аннотацию веб-ресурса - это на самом деле формально представленное знание, (частично) содержащиеся в этом ресурсе.
Семантические аннотации записываются в соответствующем языке представления знаний. Обычно используются концептуальные языки, основанные на терминологической логике (или логике описаний - description logic) [1].
В простейшем случае семантическая аннотация представляет собой список терминов (в данном языке терминологической логики) и утверждений. Например, мы можем задать термин Менингит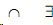 
причина.Вирус 
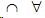причина.Вирус, (1) который обозначает менингит, вызываемый вирусом и только вирусом. Другими словами, этот термин определяет вирусный менингит, и мы можем записать утверждение
Вирусный Менингит = Менингит причина.Вирус причина.Вирус (2)
Таким образом, предложение выражает утверждение о кореферентности (синонимии) атомарного термина Вирусный Менингит и составного термина (1).
Между терминами также можно устанавливать отношение включения: t1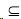 
t2, если класс объектов, определяемый термином t1, содержится в классе объектов, определяемом термином t2. Другими словами, если t1 t2, то термин t2 является более общим, чем термин t1.
Совокупность терминов и утверждений указанного вида, записанных для данной области, составляет онтологию этой области.
Ключевым понятием аннотированных ресурсов в Интернете является релевантность терминов. Степень релевантности ρ (t1,t2) - это некоторое число из интервала [0,1]. Если ρ(t1,t2)=1, то эти два термина кореферентны (что означает их полную релевантность); если ρ(t1,t2)=0, то термины не релевантны.
Как отметил Заде в [2]: «Релевантность - центральное понятие для поиска. Фактически, начальный успех Google в большой мере обязан простому, но хитроумному алгоритму ранжирования в соответствии с оценкой релевантности».
Онтологию можно рассматривать как граф, вершинами которого служат термины, а дуги отвечают отношению непосредственного следования по включению. Релевантность можно определить, используя заданную на этом графе метрику. Конечно, такого типа релевантность является лишь некоторым приближением. Формальная экспликация понятия релевантности является весьма трудной задачей. Заметим, что Заде относит это понятие к нечетким.
В настоящее время комитет W3C (World Wide Web Consorcium) в качестве стандарта для языков спецификации веб-онтологий предложил язык OWL (Ontology Web Language). На самом деле OWL имеет три диалекта: OWL Lite, OWL DL и OWL full. Эти диалекты связаны последовательно отношением синтаксического и семантического включения. Таким образом, если это отношение обозначим символом <, то будем иметь: OWL Lite < OWL DL < OWL Full. Эти языки, однако, имеют некоторые недостатки:
- атрибуты объектов представляются как роли, что не естественно, когда значением атрибута является тип данных;
- отсутствуют средства для спецификации составных типов данных, а это затрудняет совместимость онтологий с объектно-ориентированными базами данных.
2. Составление онтологий на основе Бинарной Модели Знаний
Мы предлагаем использовать для составления онтологий в области биологии и медицины язык «Бинарная Модель Знаний» (БМЗ) [3], [4]. БМЗ лишен вышеуказанных недостатков языков OWL.
Онтология (концептуальная схема), записанная в БМЗ, содержит два вида понятий: классы и бинарные связи. (Заметим, что связи могут также выступать в роли классов.) Структура понятий (универсумы понятий) задается с помощью структурных предложений, имеющих следующий абстрактный синтаксис.
• Элементарными структурными предложениями являются:
C[A:T], C[A:D], C[A:D(*)], C[A:D(m,n)], (C L D).
Здесь C и D - имена понятий (классов или бинарных связей), L - имя бинарной связи, А - имя атрибута, Т - спецификация типа данных (значений атрибута), m ≤ n - натуральные числа. Выражение D(*) обозначает понятие, экземплярами которого служат конечные множества экземпляров понятия D, а экземплярами понятия D(m,n) являются те экземпляры понятия D(*), число элементов в которых не меньше, чем m и не больше, чем n. Атрибуты можно обозначать теми же именами, что и понятия. Например, выражение C[E:E] - допустимое обозначение для элементарного структурного предложения (но вместо него можно писать просто C[E] ).
• Произвольные структурные предложения получаются соединением «хвостов» элементарных предложений с одинаковыми «головами».
Например, соединяя элементарные предложения C[E], C[K:Integer], C[A: D(*)] и С[B: (Integer(*), LIST(String)], получаем структурное предложение C[E, K: Integer, A: D(*), B: (Integer(*), LIST(String)]. Это предложение определяет универсум UC понятия С, элементами которого являются кортежи [E: x, K: y, A: z, B: u], где x - суррогат (системное имя - идентификатор объекта), y - целое число, z - конечное множество суррогатов, u - элемент абстрактного типа данных (Integer(*), LIST (String)).
БМЗ включает язык для спецификации типов данных. Типы данных могут быть примитивными (такими, как Integer, String и т.п.) или составными, т.е. абстрактными типами данных, определяемыми экспертом при помощи заданных конструкторов типов. Для спецификации операций, действующих на абстрактном типе данных используется подъязык функционального программирования. Этот подъязык играет роль хостязыка. БМЗ также включает запросный язык (к базам данных, структурированным в соответствии со подсхемами структурной спецификации).
Спецификация экстенсионалов понятий дается при помощи следующих типов предложений:
- логические предложения. Примером является предложение вида EACH C(α) L SOME D(β), где α и β - атрибутные условия;
- предложений, специфицирующих поведение объектов.
Примером являются продукция
X IN C(α), Y IN D(β) ==> DELETE f(X,Y) FROM E;
INSERT g(X,Y) INTO; ASSERT φ,
где f и g - функции, выраженные в хост-языке, а φ - логическое или модальное предложение) ;
- модальных предложений. Примером является
FUTURE EXIST X IN С(K=0) AND f
(X) =/= 1.
Замечание. Для того, чтобы сделать предложения БМЗ более читаемыми, мы можем использовать конкретный синтаксис, близкий, например, к тому, который обычно применяется в объектно-ориентированных базах данных и знаний, в частности, в такой системе как DEGAS, [5].
В БМЗ имеются две стратегии вывода (логической дедукции): прямой и обратный вывод. Прямой вывод имеет преимущество перед обратным выводом в зависимости от того, когда решается задача противоречивсти схемы. Но при вычислении ответов на запросы более эффективен обратный вывод.
Приведем пример онтологии, записанной в языке БМЗ.
Болезнь[Этиология: Фактор (*), Характер_течения: String,
Способы_лечения: Способ_лечения (*),
Патологич_изменения:Орган (*),...], (Орган Входит_в Система),
Система ISA Нервная_система | Иммунная_система |
Пищеварит _ систем а | Ре спираторная_система |
Мышечная_система | Гормональная_система |...
Внутренняя_болезнь ISA Болезнь,
Внутренняя_Болезнь[Категория: (Гастроэнтерология |
Гематология|Кардиология|Нефрология |Пульмонология)],
Место_поражения:
Орган(*)],
Гепатит ISA Внутренняя_болезнь,
Печень ISA Орган,
Гепатит = Внутренняя_болезнь (Место_поражение = Печень) Вирусный_гепатит = Гепатит (Этиология.Фактор = Вирус),
Г е п а т и т _ С = В и р у с н ы й _ г е п а т и т
(Вирус.Назв = С).
Работа выполнена при финансовой поддержке РФФИ (проект № 08-0100465)
СПИСОК ЛИТЕРАТУРЫ:
- Baader, D. Calvanese, D. McGuinness, D.Nardi, P. Patel-Schneider (eds.) The Description Logic Handbook (theory, implementation and applications). - Cambridge University Press, USA, 2003.
- L.A. Zadeh. From search machine to question answering systems - problems of world knowledge, relevance and precisiation. In: E. Sanchez (ed.) Fuzzy Logic and th Semantic Web. - Elsevier, 2006.
- G.S. Plesniewicz. Binary Data and Knowledge Model // Proceedings of the 6th Joint Conference on Knowledge-based Software Engineering, IOS Press, 2004.
- Г.С. Плесневич. Бинарная модель знаний // III-й Международный научнотехнический семинар «Интегрированные модели и мягкие вычисления в искусственном интеллекте». Сб. научных трудов (Коломна, май 2005). - М: Физматлит, 2005.
- J. van den Akker, A. Siebes. DEGAS: a database of autonomous objects // Information Systems, v. 22, No. 3, 1997.