Объекты моделирования представлены в виде трех множеств: M1 - множество людей, прошедших отбор и рассматриваемых в качестве претендентов на множество M2 . Элементами множества M2 являются вакантные (условно вакантные) должности, которые включены в бизнес-план данной организации. M3 - множество видов обучения, выполняющих поддерживающую функцию, функцию социализации и мотивации представителей множества M1 [1]. Элементами множества M3 являются виды начального, повторного и развивающего обучения: рабочий инструктаж, ротация должностей, обучение в учебном центре на базе организации, обучение в вечерней школе, обучение на курсах повышения квалификации и переподготовки кадров, обучение в лицеях, колледжах, ВУЗах и академиях.
Сформулируем следующую задачу. Претендента из M1 , прошедшего определенный вид обучения из M3 , назначить на соответствующую его способностям, образованию и ожиданиям должность из M2 . Результатом такого назначения должно стать повышение эффективности деятельности организации, выраженное в повышении общего уровня выполнения работы, реализации профессионального потенциала каждого сотрудника и формирования резерва талантливых людей, способностями которых организация могла бы воспользоваться в будущем. С точки зрения математического моделирования эта задача представляет собой обобщение известной в теории дискретной оптимизации задачи о назначениях [5]. При определении допустимых решений этой задачи должны быть учтены ограничения на финансовые, производственные, трудовые и временные ресурсы, имеющиеся в распоряжении данной организации. Качество этих решений оценивается как экономическими (в рублях), так и социально-психологическими критериями. Значениями социально-психологических критериев могут служить результаты тестов (в баллах), которые проводятся для оценки детерминант, определяющих уровень и качество выполнения работы. Например, такими детерминантами в [1] являются способность, готовность и возможность выполнять работу. Таким образом, рассматриваемая задача формулируется как многокритериальная.
В предлагаемой математической постановке задачи используются следующие понятия и обозначения теории гиперграфов [2]: G = (V,E) - гиперграф с множеством вершин V = {v} и множеством ребер E = {e} ; ребра e ∈ E представляют собой подмножества множества V, т.е. e ⊆ E.
Если каждое ребро e ∈ E гиперграфа G состоит из λ вершин, то гиперграф G называют λ-однородным. При λ=3 гиперграф G будем называть 3-однородным; 3-однородный гиперграф G называется 3-дольным, если множество вершин V разбито на три подмножества Vs , s= 
так, что в каждом ребре e = (v1, v2, v3) ∈ E его вершины принадлежат различным долям, т.е. vs ∈ Vs, s = . В этом случаем гиперграф G будем обозначать через G = (V1,V2,V3,E). Если в паре ребер e 1, e2 ∈ E нет общего для них элемента v ∈ V, то эти ребра называются непересекающимися. Всякое подмножество попарно непересекающихся ребер называется паросочетанием данного гиперграфа G . Это паросочетание называется максимальным, если оно содержит максимальное число ребер и называется совершенным, если каждая вершина инцидентна [2] некоторому ребру паросочетания.
В качестве иллюстративного примера рассмотрим гиперграф
G = (V1,V2,V3,E), V 1={1,2,3,4}, V2 ={5,6,7}, V3 = {8,9,10,11}, E = {e 1,e2,...,e5}, где e 1 =(1,5,9), e2 =(3,6,10), e3=(4,7,11), e4 = (1,7,10), e5 = (2,5,8), представленный на рис. 1.
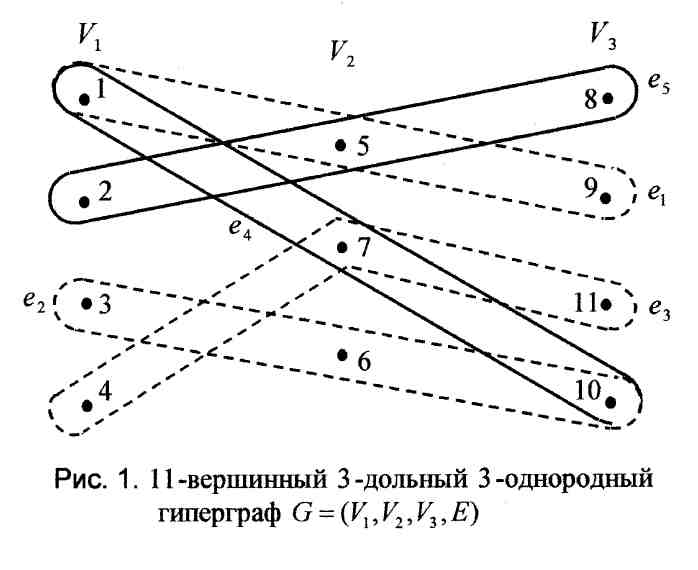
Нетрудно увидеть, что в рассматриваемом гиперграфе имеются три тупиковых паросочетания E 1 = {e 1,e2,e3}, E2 = {e2,e3,e5}, E 3 = {e4,e5}, Ei ⊂ E, i = . Паросочетание E0 ⊂ E называется тупиковым, если любое ребро e∈(EE0) пересекается хотя бы с одним ребром из E0 . Отметим что максимальное (совершенное) паросочетание согласно этого опреде-ления, также является тупиковым. Гиперграф, изображенный на рис. 1, содержит два максимальных паросочетания E1 и E2.
Математическая постановка рассматриваемой задачи базируется на 3-дольном 3-однородном гиперграфе G = (V1,V2 ,V3 ,E ) , который определяется следующим образом. Вершины первой доли V1 (второй доли V2 ) поставлены во взаимнооднозначное соответствие указанному выше множеству претендентов M1 (множеству должностей M2 ), т.е. имеет место равенство мощностей: |V1| =|M1 | (| V2| =|M2 |). Вершины третьей доли V3 отражают множество видов обучения претендентов с учетом представленных выше ограничений следующим образом. Пусть элементы множества M3 перенумерованы индексом r = 1,2,...,L, и для каждого значения r определено максимально возможное количество mr людей, для которых организация может осуществить r -й вид обучения; обозначим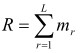 
. Каждому индексу r = 1,2,...,L поставим в соответствие множество 
мощности | | =mr.. Тогда третья доля V3 определяется как теоретико-множественное объединение всех множеств , т.е.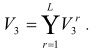 
Рассмотрим пару элементов v1 ∈V1, v2 ∈V2, где v1 означает определенного претендента, а v2 представляет определенную должность. Тогда, если кандидат v 1 может заполнить вакансию v2 после прохождения r -го вида обучения, согласно стратегии принятия решений о распределении вакантных должностей в данной организации [1], то считаем, что множество E содержит mr ребер вида
(1)
В противном случае множество E не содержит ни одного ребра вида (1). Ребро вида (1) условимся называть допустимой тройкой. Множество E всех ребер гиперграфа G = (V1,V2,V3,E ) , 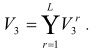образуется в результате теоретико-множественного объединения допустимых троек вида (1) по всем элементам 
В классической постановке задачи о назначениях, сформулированной на 2-дольном графе, как правило, термин "допустимое решение" означает совершенное (максимальное) паросочетание на этом графе. Допустимым решением рассматриваемой задачи на гиперграфе является всякое тупиковое паросочетание. Для данного гиперграфа G = (V,E) тупиковое паросочетание представляем в виде его подгиперграфа
Каждому ребру e <Е E вида (1) гиперграфа G = (V,E) приписаны два веса wv (e), V = 1,2 , которые означают w1 (e) = f1 (v1, v2, v3) - экономический эффект, т.е. ожидаемый доход организации (в рублях) в случае, когда претендент, представленный вершиной v1, прошел вид обучения, представленный вершиной v3, и назначен на должность, представленную вершиной v2; w2 (e) = f2 (v 1, v2, v3) - социально-психологический эффект, т.е. ожидаемый уровень социализации [1] претендента (в баллах) в этом же случае.
Качество допустимых решений этой задачи xеX оценивается с помощью векторной целевой функции (ВЦФ)
F(x) = (F1(x),F2(x)), (2)
состоящей из критериев вида MAXSUM
. (3)
Критерий F1 (x) означает ожидаемый суммарный доход организации от указанного выше назначения. Критерий F2 (x) означает ожидаемый уровень социализации всех претендентов, назначенных на соответствующие должности.
ВЦФ (2) - (3) определяет в МДР X паретовское множество (ПМ) X, состоящее из паретовских оптимумов (ПО) 
[3]. В случае, если одинаковые по значению ВЦФ решения x´, x" ∈ X считаются эквивалентными (неразличимыми), то из ПМ 
выделяется полное множество альтернатив (ПМА) X0 . ПМА X0 представляет собой максимальную систему векторно несравнимых ПО из , X0 ⊆ .
Наиболее целесообразное решение выбирается из ПМА с помощью процедур теории выбора и принятия решений [4].
СПИСОК ЛИТЕРАТУРЫ:
- Джуэлл Л. Индустриально-организационная психология. 2001. СПб.: Питер. 720 с.
- Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. 1990. М.: Наука. 384 с.
- Емеличев В.А., Перепелица В.А.//Дискретная математика. 1994. Т. 6. вып. 1.С. 3.
- Ларичев О.И. Наука и искусство принятия решения. 1979. М.: Наука. 200 с.
- Сакович В.А. Исследование операций.1984. Минск.: Вышэйшая школа. 256 с.