Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

 Лес пространство, покрытое растущими и рослыми деревьями В.И. Даль

Теоретический анализ. Растущие и рослые деревья по В.И. Далю образуют основу пространства леса. Расти - вырастать, возрастать, увеличиваться питаньем, а рослый - взрослый, во всех годах. Издревле дерево понималось как живое и здоровое растенье, причем большое, высокое и крупное.

Совокупность деревьев - основа формирования леса как экосистемы.

Определение леса как экосистемы, данное в Лесном кодексе, расширяет объем понятия (ныне лес даже лесоводы понимают как склад древесины и как вертикально стоящие бревна) растущих и рослых деревьев. По В.И. Далю молодое насаждение не являются лесом, а лесишком, где сообщество деревьев еще не способно организовать внутри себя пространство флоры и фауны, то есть не способно стать лесом.

В средневозрастных древостоях, как будет показано в статье, действие растительной силы, то есть активности питания и усвоения питательных веществ в прирост себе, можно оценивать простыми математическими зависимостями. К кривой высот [1, c.19-20], то есть зависимости высот деревьев Н от диаметра ствола D₁₃ на высоте 1,3 м, нами дополняется кривая диаметров (толщин), то есть зависимость толщины ствола от высоты деревьев.

Таким образом, кривая высот типа H = f(D₁₃) характеризует рослость деревьев на выделе леса (по экспериментам на пробной площадке древостоя). А кривая толщин типа D₁₃ = f(H) показывает (в общем случае на любой высоте стволов) не только рост, но и состояние структурного развития деревьев стволами и кронами внутри пространства древостоя. Обе эти кривые  позволяют измерять территориальное и компонентное экологическое равновесие (экологический баланс) по Н.Ф. Реймерсу [10, с.427-431].

Методика. Экологическими компонентами древостоя, как ядра лесной экосистемы, то есть леса, являются растущие и рослые деревья. Баланс между ними возникает только в девственных лесах, да и то падающие отдельные деревья образуют там дисбаланс или неравновесие на отдельных частях древостоя. Оказалось, что проще оценивать неравновесное состояние среди растущих на пробной площадке деревьев, чем найти равновесие между ними.

Для оценки компонентного экологического неравновесия древостоя предлагается применять два способа: таксационных измерений деревьев [1]  и распределений их по лентам на пробной площадке по патенту [9].

Первый способ [1, с.19-20, 179-180) включает в себя измерение диаметра D13 (см) на высоте 1,3 м и высоты H (м) от корневой шейки. После находят зависимости высоты деревьев от их диаметра по стволам в виде математической функции H = f(D₁₃) или же строят в прямоугольной системе координат по парам значений D₁₃ (ось абсцисс) и H (ось ординат) на миллиметровке кривую высот. Затем на построенной кривой отсчитывают значения высоты для каждой ступени толщины у стволов деревьев. Причем кривая высот рассматривается как кривая состояния древостоя в отличие от кривой его развития, однако при выборочных рубках деревьев, находящихся в древостое в экологическом равновесии, кривая высот совпадает с кривой развития. Неравновесие наступает после рубки или же оно уже было до неё.

Основным недостатком является применение группировки деревьев по ступеням толщины ствола, что снижает точность математического описания кривой высот по всем измеренным деревьям на пробной площадке. Выравнивание кривой высот на миллиметровке вообще не рассматриваем.

Второй способ измерения растущих деревьев по патенту 2229127 [9] предполагает разметку на пробной площадке параллельных лент, на которых сосчитывают оставленные после рубок ухода деревья, измеряют параметры, проводят анализ распределения значений таксационных показателей по лентам. Здесь недостатком является отсутствие оценки параметров деревьев на пробной площадке в целом по кривым состояния (высот и диа
метров), причем эти кривые состояния деревьев на лентах не сравниваются с кривыми состояния всех измеренных деревьев, например, до и после рубок прореживания и проходных.

Для повышения контроля за рубками деревьев и комплексности оценки экологического состояния древостоя, вначале на пробной площадке измеряют толщины ствола и высоты всех деревьев. Затем идентифицируют  закономерности  типа H = f(D₁₃) и D₁₃ = f(H)  для сопоставления каждой ленты со всей пробной площадкой.  А по результатам сравнения этих закономерностей до и после проведения рубок деревьев оценивают качество проведения прореживания леса или проходных рубок. Поэтому способ [9] с уточнениями рекомендуется к применению в лесничествах, например, при контроле за выполнением проектов освоения лесов рубками ухода.

Экспериментальная часть. После рубки прореживания в  кв. 34 выделе 65 Кокшамарского лесничества Кокшайского лесхоза Республики Марий Эл в 2006 году на пробной площадке 20*60 м, расположенной от края лесной дороги, были измерены 114 деревьев (табл. 1). В среднем плотность популяции оставленных на дальнейшее доращивание деревьев сосны составляет 950 шт. га ^-1. По количеству пней 108 шт. до рубки на пробной площадке росли 222 дерева (плотность древостоя 1850 шт. га ^-1).

На рис. 1 приведена кривая высот для всех оставленных после рубки прореживания деревьев на пробной площадке по данным табл. 1, а на рис. 2 - кривая диаметров по этим же данным. При этом уравнения высот и диаметров идентифицируются одной и той же закономерностью [2 8] типа:

- статистическая закономерность кривой высот (рис. 1)

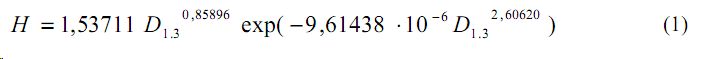
Таблица 1. Таксационные показатели растущих деревьев на пробной площадке 20*60 м

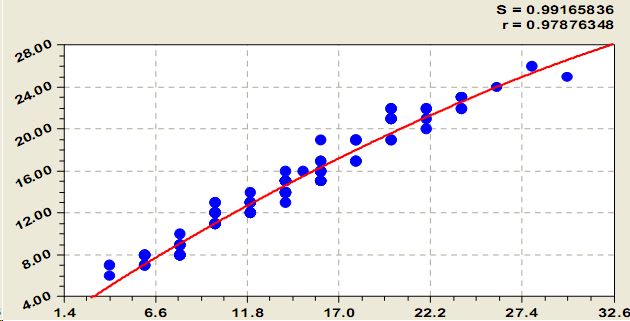
Рис. 1. Кривая высот у растущих на площадке деревьев сосны

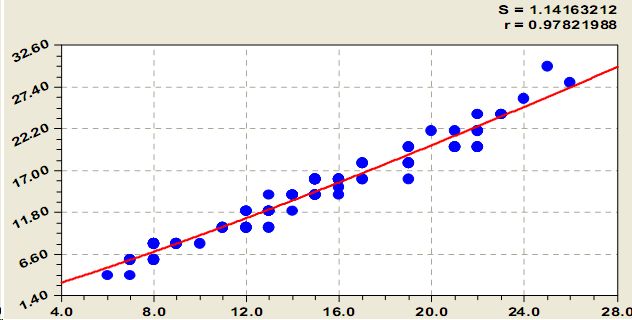
Рис. 2. Кривая диаметров на высоте 1,3 м у деревьев сосны

- математическая модель кривой диаметров растущих деревьев (рис. 2)

Уравнение (2) является показательным законом, который  по конструкции становится частным случаем более общего биотехнического закона [2 8], выраженного в виде формулы (1). В ней по сравнению с уравнением (2) появилась вторая компонента в виде закона экспоненциальной гибели, то есть рост в высоту происходит, по сравнению с ростом по диаметру, с торможением.

Коэффициенты корреляции у формул (1) и (2) почти одинаковы и соответственно равны 0,979 и 0,978.

Рослые деревья (лидеры по высоте) по рис. 1 образуют подгруппу из верхних точек, а крупные деревья (лидеры по толщине) образуют множество из верхних точек рис. 2:

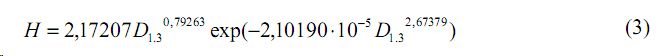
лидеры по толщине ствола (22 крупные деревья), r = 0,998

В некоторых странах, например в Англии, для оценки древостоя принимают только деревья лидеры по высоте,  что значительно снижает трудоемкость измерений.

Распределение деревьев по лентам. По патенту [9] эффективно оценивать древостой на пробной площадке по отдельным лентам (рис. 3).

После моделирования идентификацией биотехнического закона были получены следующие формулы для лент пробной площадки:

-первая лента леса, коэффициенты корреляции 0,975 и 0,975

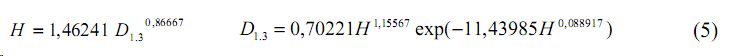
- вторая лента леса, коэффициенты корреляции 0,980 и 0,981

-третья лента леса, коэффициенты корреляции 0,974 и 0,974

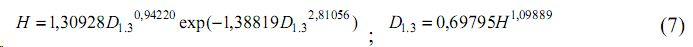
- четвертая лента леса, коэффициенты корреляции 0,988 и 0,990

- пятая лента леса, коэффициенты корреляции 0,983 и 0,984

- шестая лента леса, коэффициенты корреляции 0,986 и 0,965

Схемы точечных кривых высот и диаметров показаны на рис. 4

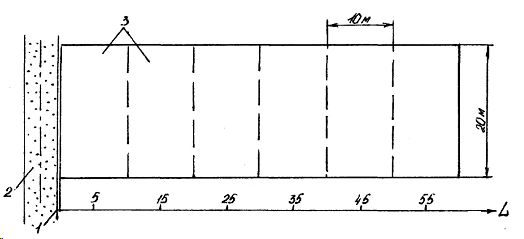
Рис. 3. Схема расположения пробной площадки около лесной дороги:

1 - граница пробной площадки; 2 - лесная дорога; 3 - ленты леса

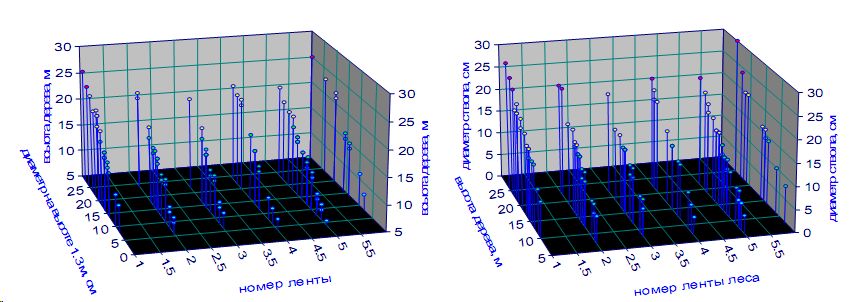
Рис. 4. Двухфакторные графики: а - кривой высот; б - кривой диаметров ствола на 1,3 м

Парное сравнение формул (5 10 показывает почти одинаковую адекватность закономерностей изменения высот и диаметров друг от друга.

Коэффициент компонентного экологического неравновесия. Отношение остатков  ε  к  расчетным  значениям (1 10 назовем коэффициентом неравновесия К_н. Но, как оказалось, сами остатки ε могут быть смоделированы волновыми функциями, основанными на биотехническом законе [2 -8]. Тогда компонентное экологическое неравновесие К_н по состоянию на момент измерений растущих деревьев определяется формулой

где y₁ не волновая первая составляющая статистической закономерности, показывающая естественную растущую силу деревьев на момент измерений (может быть и больше одной составляющей); y₂, y₃  волновые составляющие колебательной адаптации популяции деревьев по общей растущей силе.

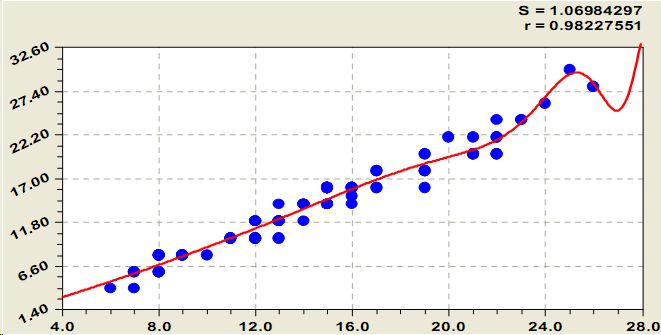
Рис. 5. Рой точек и график кривой высот 114 деревьев сосны

Волновые составялющие кривых состояния.  Кривая высот с волновой составляющей получает вид (рис. 5) составного уравнения

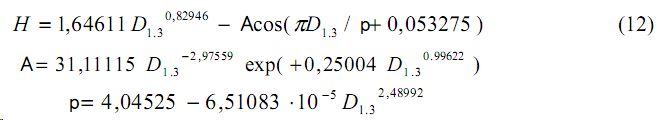
где A - амплитуда колебательного возмущения деревьев по высоте, м;

p - половина периода колебательного возмущения по высоте, м.

Из-за смены знаков амплитуда изменяется по аномальному биотехническому закону [2 -8], а частота возмущения у рослых крупных деревьев учащается. Первая составляющая имеет показательный рост.

Кривая диаметров получает выражение (рис. 6) вида

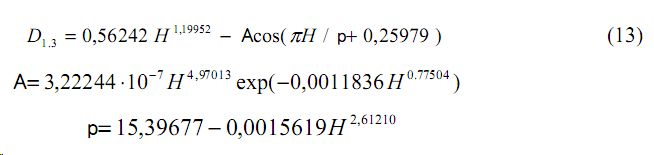
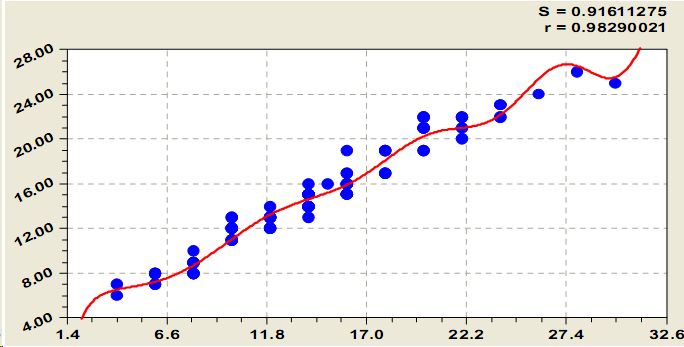
Рис. 6. Рой точек и график кривой диаметров 114 сосен на пробной площадке 20*60 м

Кривые диаметров стволов растущих деревьев на уровне 1,3 м от корневой шейки (основной экологический горизонт) показывает позитивные возможности дальнейшего роста оставшихся после прореживания деревьев сосны (вторая составляющая не аномальна).

Оценка качества рубок ухода. Пусть неизвестно исходное состояние кривых диаметров по пробной площадке до проведения рубки прореживания. Тогда предлагается заложить пробную площадку по схеме на рис. 3, измерить растущие деревья и найти кривые диаметров по лентам леса с волновыми составляющими по обобщенной формуле

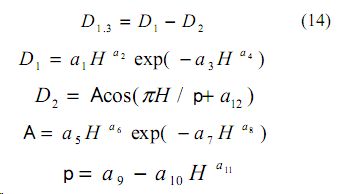
где a1...a12 искомые параметры статистической модели (20).

На рис. 7 приведены графики кривых диаметров по шести лентам.

Качество множеств деревьев на лентах (рис. 7) и в целом по пробной площадке (см. рис. 5 и рис. 6) определяется по характеру изменения кривых высот и диаметров в правом верхнем углу. Растительная сила по пробной площадке положительная, т. к. кривые на рис. 4 и рис. 5 продолжатся, по мере дальнейшего роста оставленных после рубки деревьев, вверх.

Однако по лентам картина иная: на лентах № 1, 3 и 5 деревья будут расти устойчиво по толщине, а деревья, расположенные на лентах № 2, 4 и 6 будут расти явно неустойчиво. Причем на второй ленте неравновесие наблюдается на рослых и крупных деревьях сосны.

В табл. 2 приведены результаты вычислений коэффициента неравновесия (11) по заданным моделям (20) кривых диаметров стволов 114 сосен. Для расчетов достаточно знать параметры первой составляющей модели (14), а при явной динамичности неравновесия волновые составляющие не ищутся и достаточно использовать только трендовые закономерности типа (2 -10), если максимальные остатки трендов составляют не менее 40 %.

Лидером по росту в толщину (+44,99 % от среднестатистической кривой диаметров на ленте № 1) является дерево, когда при высоте 13 м ствол сосны достиг диаметра 14 см на высоте 1,3 м от корневой шейки. Аутсайдером по росту в экологическом горизонте (-35,77 % от кривой диаметров на ленте № 4) является сосна высотой 7 м, а диаметром всего 4 см.

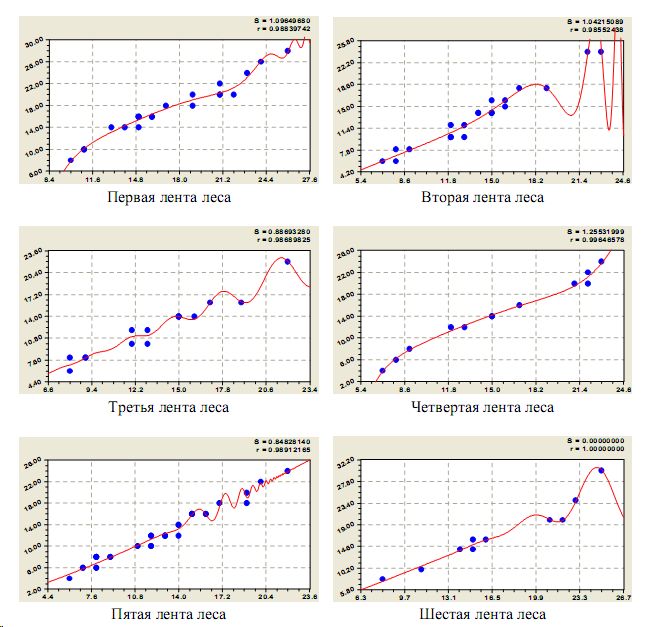
Рис. 7. Кривые диаметров по лентам пробной площадки 20*60 м

Обсуждение результатов. Таким образом, в высоту и в толщину действует одинаковый закон, математически состоящий из мультипликации двух устойчивых законов показательного роста и экспоненциальной гибели (спада). Модель показательного структурного развития (роста в толщину) даже точнее по коэффициенту корреляции на первых трех лентах леса по сравнению с ростом высоту.

По распределениям остатков после формул (5 -16) можно судить о пространственной организации деревьев и мест их произрастания.

При этом точность измерений (для диаметров была принята точность ±0,5 см, а для высот - ±0,5 м) существенным образом влияет на распределения остатков ε = у_ф ·у (абсолютных погрешностей) найденных формул, где: у_ф - фактические значения параметров деревьев по табл. 1; y - расчетные значения параметров деревьев по формулам (1-10).

Таблица 2. Параметры первой составляющей модели (20) по лентам леса на пробе 20*60 м и коэффициент неравновесия по лидерам и аутсайдерам деревьев сосны

Примечания: * шесть деревьев; полужирным шрифтом выделены максимальные значения высоты и толщины ствола у лидера и аутсайдера из 114 сосен по крупности (относительно высоты дерева) диаметра

Предложенный коэффициент неравновесия можно определить в целом по пробной площадке (или же по результатам ленточного или полного перечета деревьев во всем древостое), а также по лентам леса на пробной площадке, сориентированной  относительно  лесной  дороги (в общем случае относительно любых лесных объектов). Значимое неравновесие среди растущих деревьев наблюдается по кривым диаметров, когда появляется возможность моделирования волновых составляющих закономерности (20) при условии, если остатки от тренда составляют менее 40 % от самого тренда.

Основные выводы и рекомендации. Коэффициент компонентного экологического неравновесия позволит оценивать не только структурное качество древостоя и проведенных рубок ухода за лесом, но и оценивать влияние лесных дорог, квартальных и иных просек, зданий и соору
жений, холмов и оврагов, а также других объектов, находящихся в лесном массиве. При малом экологическом неравновесии этот коэффициент определяется по формуле (11), а при больших колебательных возмущениях параметров растущих деревьев он может вычисляться упрощенно как отношение остатков от трендовой закономерности типа (1 10) к расчетным значениям по ней.

Предлагаемый способ по патенту [9] относится: во-первых, к лесоведению, в частности к изучению свойств древостоя с различными антропогенными сооружениями внутри и по краям; во-вторых, к лесоводству, в частности к слежению ха ходом роста и развития лесных культур; в-третьих, к прижизненному лесопользованию, например, к оценке качества проводимых и проведенных технологических мер в древостое. Этот способ может быть использован, например, при оценке каче 

ства древостоя до и после рубок в средневозрастных и приспевающих древостоях, а также для обоснования экологических требований и выбора рациональных процессов и технических комплексов для рубок прореживания и проходных.

Для лесничеств способ рекомендуется при сертификации участков леса. Он, с учетом оценки по коэффициенту неравновесия, может быть использован при мониторинге особо охраняемых территорий с древостоями, нуждающимися в санитарных выборочных рубках.

СПИСОК ЛИТЕРАТУРЫ:

1. Анучин Н.П. Лесная таксация: Учебник для вузов. - Изд. 5-е, дополнен. / Н.П. Анучин. - М.: Лесная промышленность, 1982. - 552 с.
2. Бедертдинов Э.Н. Циклическое размещение деревьев после рубок ухода / Э.Н. Бедертдинов // Материалы VI междунар. конф. "Циклы природы и общества". Часть 2. Ставрополь: Изд-во Ставроп. ун-та, 1998. С.179-182.
3. Мазуркин П.М. Геоэкология: Закономерности современного естествознания: Научное изд. / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с.
4. Мазуркин П.М. Математическое моделирование. Идентификация однофакторных статистических  закономерностей:  учебноетпособие / П.М. Мазуркин, А.С. Филонов. -Йошкар-Ола: МарГТУ, 2006. - 292 с.
5. Мазуркин П.М. Статистический мониторинг рубок ухода за лесом / П.М. Мазуркин, Э.Н. Бедертдинов // Тр. междунар. конф. "Математические и физические методы в экологии ..." М.: МГУЛ, 2001. С.269-274.
6. Мазуркин П.М. Оценка и прогноз качества лесной территории / П.М. Мазуркин, Э.Н. Бедертдинов, П.А. Перов // Лесной журнал. - 2003. № 4. - С. 33-41.
7. Мазуркин П.М. Динамика рубок леса / / П.М. Мазуркин, Э.Н. Бедертдинов, А.Н. Фадеев. - Йошкар-Ола: МарГТУ, 2002. - 216 с.
8. Мазуркин П.М. Изменение площади места произрастания лидирующего дерева / П.М. Мазуркин, Н.В. Русинова // Лесной журнал. 2001. № 1. С. 14-20.
9. Пат. 2229127 Российская Федерация, МПК7 G 01 N 33/46, А 01 G 23/00. Способ испытания растущих деревьев после рубок прореживания и проходных / Мазуркин П.М., Колесникова А.А. Бедертдинов А.Н. Русинова Н.В. (РФ); заявитель и патентообладатель Марийск. гос. тех. ун-т. № 2001115403/12; заявл. 04.06.01; опубл. 20.05.04. Бюл. № 14.
10. Реймерс,  Н.Ф.  Природопользование: Словарь-справочник  /  Н.Ф.  Реймерс. М.:Мысль, 1990. - 637 с.

Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603 МОН РФ