В списке процедур и функций рекомендуется описать следующие функции:
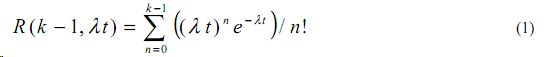
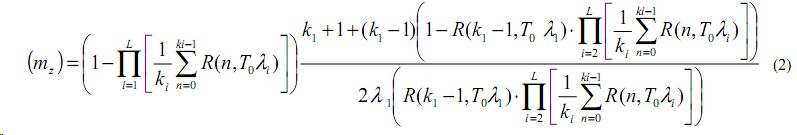
где Т0 - среднее значение приемлемого для продолжения движения интервала по времени между автомобилями (постоянная величина).
1-й шаг. Вводим следующие данные для одного из вариантов организации движения на данном нерегулируемом перекрестке:
- тип перекрестка (крестообразный или Т-образный);
- количество полос для движения в каждом направлении;
- интенсивность по каждому из направлений движения.
2-й шаг. Создаем массивы, хранящие параметры распределения Эрланга. Экспериментально доказано, что можно принять параметр k=2, параметр λ рассчитывается следующим образом:
![]()
где Ni - интенсивность движения по i - ой полосе.
3-й шаг. Для каждого из направлений движения по второстепенной дороге рассчитываем среднее время ожидания первым в очереди автомобилем возможности пересечь главную дорогу по формуле (2).
4-й шаг. Если параметр α = λ*m/k < 1 , то для каждого направления движения по второстепенной дороге рассчитываем:
- среднюю задержку (в секундах) автомобилей в данном направлении:
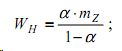
- среднюю длину очереди в данном направлении:
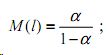
- вероятность отсутствия очереди в данном направлении
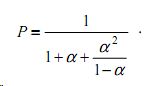
- среднюю суммарную потерю времени (авт-ч) всех автомобилей на данном перекрестке за один час:
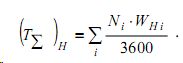
Если параметр α>1, то вычисляем приблизительную нижнюю границу этих характеристик по вышеперечисленным формулам, приняв α=0,9.
5-й шаг. Рассчитываем следующие средние характеристики:
- средняя суммарная потеря времени (авт-ч) всех автомобилей на данном перекрестке за один час
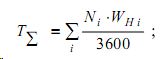
- средняя задержка (в секундах) автомобилей второстепенного направления
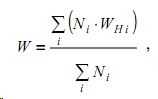
где Ni интенсивности движений по полосам второстепенного направления, WHi соответствующие средние задержки.
6-й шаг. Выводим на экран результаты расчетов.
7-й шаг. Повторяем шаги 1-6 для каждого из возможных вариантов организации движения на данном нерегулируемом перекрестке.
8-й шаг. По заданному пользователем с клавиатуры критерию К выбираем оптимальный вариант:
- если К={средняя задержка автомобилей в данном направлении }, то оптимальный вариант отвечает условию min{WHi};
- если К={средняя задержка автомобилей второстепенного направления}, то оптимальный вариант отвечает условию min{W};
- если К={ средняя суммарная потеря времени всех автомобилей на данном перекрестке за один час }, то оптимальный вариант отвечает условию min{TΣ}.
Работа выполнена при поддержке РФФИ.



