Расстояние между электродами, один из которых прозрачен для видимой части спектра излучения, обычно не превышает 1 см. Газовый разряд в ГРП инициируется рентгеновским или высоко энергетическим тормозным излучением. После подачи на электроды импульса высокого напряжения, из областей первичной ионизации в газе развиваются электронные лавины, что приводит к усилению изображения. На начальной стадии своего развития газовый разряд качественно может быть описан в соответствии с таундсендовским механизмом развития газового разряда[1]. Механизм Таунсенда при описании разряда справедлив до тех пор, пока можно пренебречь электрическим полем пространственного заряда электронов и ионов по сравнению с напряженностью внешнего поля. Экспериментальные исследования [2] показали, что вследствие искажения поля пространственными зарядами, уже при небольшой плотности тока 10-8 А/см, наступает заметное увеличение ионизации, и условия самостоятельности разряда выполняется при меньших значениях напряженности на разрядном промежутке.
Для описания разряда этих условиях наиболее широко используется теория искрового разряда, разработанная Миком [3] и независимо от него Ретером [4], которая основана на многочислимых экспериментальных исследованиях развития искрового разряда.
С помощью этого механизма можно устранить противоречия, связанные с очень малы коэффициентом поглощения в опытах Ретера и других авторов [5]. В качестве ионно-молекулярной химической реакции, способной объяснить механизм развития катодного стримера в гелии, предложена ассоциативная ионизация:
Например, для гелия сечение реакции имеет значение ≈10 -15 -10 -16 см2 [15]. Исследуем реакцию типа (1) как один из возможных механизмов развития стримера в условиях ГРП с ксеноновым наполнением. Учитывая селективность реакции (1), при протекании в собственном газе ассоциативную ионизацию более правильно записать в виде:
Индексами n и θ обозначают соответственно состояния возбужденного атома и номера колебательного уровня иона A2+ , σ n,v сечение процесса (1). Ассоциативная ионизация осуществляется, если энергия возбужденного атома A* превышает энергию основного колебательного состояния θ = 0 иона A2+ . Вообще говоря, столкновения атомов A* и A может привести к появлению A* (θ) в различных колебательных состояниях, поэтому процессу (2) можно сопоставить сечение в соответствии с набором начального и конечного каналов реакции. В настоящее время, однако, сведения о выходе ионов A в зависимости от θ при ассоциативной ионизации атомов инертных газов отсутствуют. Поэтому реакцию (2) будем характеризовать суммарным сечением:
Лишь для атомов гелия имеются наиболее подробные экспериментальные и теоретические данные [6]. В этой же работе отмечается, что ассоциативная ионизация становится преобладающим каналом разрушения возбужденных атомов и молекул при выполнении условия
где τ * - время жизни возбужденного состояния, [A] - концентрация нормальных атомов, θa - скорость атомов. По соотношению (4) можно определить наиболее интенсивные колебательные уровни атома гелия вступающие в реакцию (2). Для других атомов инертного газа использовать (4) затруднительно из-за отсутствия данных о сечениях выхода A2 + в зависимости от θa .
В работе [7] приведен наиболее удобный для практического применения критерий по оценке протекания разрушения возбужденных атомов по типу (2), исходящий из энергетических соображений
где ε*A -энергия возбуждения частицы А, εiA – энергия ионизации этой частицы, εd(AB)+ – энергия диссоциации молекулярного иона (AB)+ на A и B. Ассоциативная ионизация наиболее эффективно происходит в случае, когда потенциал ионизации атома сравним с энергией диссоциации молекулярного иона. У атомов инертных газов наиболее благоприятными для ассоциативной ионизации являются уровни, энергия возбуждения которых превышает ε* >22,19 эВ; 20,2 эВ; 14,6 эВ; 12,8 эВ;11,07 эВ соответственно для Не, Ne, Аr, Кr, Хе.
Данные предположения согласуются с исследованиями [8], где показано, что для Аr реакция (2) идет наиболее активно с участием атомов в состояниях 6S 3/2 и 4d 1/2 (энергия уровней 14,84 эВ; 14,69 эВ). Оценим количество вторичных электронов, образованных в месте образования начального электрона в результате ассоциативной ионизации. Для получения количественных оценок по образованию электронов за счет (2) необходимо знать основные параметры возбуждения атомов и молекул (сечения, функцию распределения электронов по скоростям). Непосредственное решение кинетического уравнения Больцмана для нахождения функции распределения электронов затруднительно. Однако при рассмотрении атомарного газа можно полагать, что средняя энергия электронов много меньше энергии возбуждения ато-мов ε* и составляет (3/10) ε1 : (5,0 эВ; 3,5 эВ; 3,0 эВ; 2,5 эВ – для Ne, Аr, Кr, Хе соответственно. В этом случае свободных электронов, способных возбуждать или ионизировать атом, мало, причем электрон, испытывающий неупругое соударение теряет практически всю энергию. Это позволяет использовать диффузионную модель, заключающуюся в том, что при θ < θ1 ( θ1 – скорость электронов, соответствующая началу неупругих потерь энергии) электроны накапливают энергию из-за диффузии в электрическом поле, а при θ > θ1 теряют ее в неупругих столкновениях. Используя данную модель, а также с учетом того, что vt = const с точностью 15-20% в области энергий ε1 < ε* <3 · ε1 (vt – транспортная частота упругих соударений) симметричную часть функции распределения электронов, необходимую для расчета выхода оптического излучения, можно представить в виде):
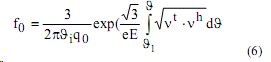
где q0 - параметр столкновений:
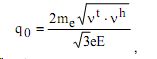
vh - частота неупругих столкновений, E - напряженность поля в газоразрядном промежутке, m e и е - масса и разряд электрона соответственно. Расчет сечений возбуждения резонансных уровней производился по формуле Режемортера с использованием экспериментальных значений сил осцилляторов [9], а оценки сечений для видимого излучения получены по полуэмпирическим формулам, разработанным Ванштейном, Собельманом и Юковым. Количество резонансно возбужденных атомов, приходящихся на один свободный электрон в лавине запишем, как [10]
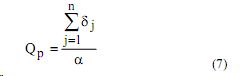
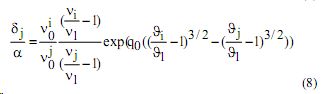
где суммирование проводилось по полному набору резонансных уровней; v j0 и v i0 - соответственно коэффициенты пропорциональности в аппроксимационных формулах для частоты возбуждения на j-й резонансный уровень и частоты ионизации, θ j и θ i - скорости электронов, соответствующие энергиям jго резонансного уровня и потенциала ионизации. Для используемой конструкции ГРП при питании прямоугольными импульсами, значения напряженности, соответствующей лавино-стримерному переходу для Nе, Аr, Кr, Хе соответственно равны: 5,6; 10,4; 11,2;14,8 кВ/см. Параметр столкновений обратно пропорционален напряженности электрического поля и при E = E n , q 0 →0 . Учитывая, что
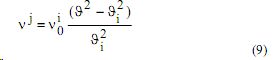
а также, что экспонента в выражении (8) при q 0 →0 стремится к 1 , получим
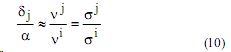
Аналогично рассуждая для расчета видимого излучения, получим
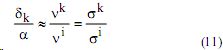
Выход видимого излучения в области E >E n отличается от удельного выхода резонансного излучения на величину
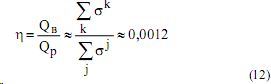
и Qв также можно считать const при En >14,8 кВ/см. Если обозначить T - характерное время реакции (3), Tp - время разряда, τc - время релаксации ступенчатых переходов, то при T <<Tp только часть возбужденных атомов успеет вступить в реакцию (2), так как τc >> Tp ( τc ≈10 -5 ). Число электронов, образовавшихся в результате ассоциативной ионизации в головке лавины с радиусом r= 0,1 мм ( r=rл - радиус лавины).
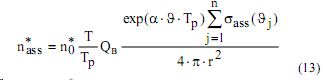
где n *0 - плотность ионизации скрытого изображения ≈108 см -3
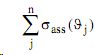- полное сечение ассоциативной ионизации ≈10 -16 см2 , T≈10 -10 с , Tp ≈10 -8 с , Qв≈ 6,5 ·10-2 фотон/электрон
Подставив данные значения в (13), получим
n*ass << 1 (14)
при любых значениях напряженности электрического поля в рабочем режиме ГРП. Условие (14) означает, что реакция, протекающая по схеме (2) и объясняющая распространение катодонаправленного стримера в гелии, в условиях ГРП не может образовывать вторичных электронов для поддержания самостоятельности разряда, так как даже в головке лавины, где плотность электронов максимальна, данный механизм не играет существенной роли в образовании вторичных электронов.
Список литературы
- Мик Дж Карэгс Дж. Электрический пробой в газах./ Перевод с англ. Под ред. В. С. Комелькова - М.:Изд.1960 г. 605 с.
- Браун С. Элементарные процессы в плазме газового разряда - М.: Госатомиздат, 1961. -323с.
- Miek J.M.//Phys .-V.57.-P.722
- Raether H. // Arch Electrotechn.-1940.-V.34.P.49.
- Ретер Г. Электронные лавины и пробой в газах./ Перевод с англ. Под ред. В. С. Комелькова .М.: Мир, 1968.-420 с.
- Леб Л. Основные процессы электрических разрядов в газах. М. -Л.: ГИТЛ, 1950. -672 с.
- Лозинский Э. Д. К вопросам о природе фотоионизирующего излучения при стримерном пробое газа // ЖТФ.-1968.-Т.38.-с. 1563-1569.
- Raether H. Ionizing Radiation Accompaming a Spark Discharge // Z. Phys. 1958. Bd 151.-P.264-276.
- Hornbeck J. A. Molnar J. P. Mass Spectrometric Studies of Molecular Ions in the Noble Gasses// Phys.Rev.-1951.V.84.-P621-625.
- Lozansky E. D. Mechanisms of Seconcary Processes in Streamer Breakdown of Gases //J. Phys. D. .1969.V.2.-P.137-148.