Применение нами стохастического системного подхода к анализу химико-технологического процесса и оборудования, в целом как физической системы, позволяет определить все внутренние связи между элементарными процессами, выявить определенные закономерности их протекания или же доказать полное отрицание их детерминированности. Этот метод позволяет дать математическое описание надежной работы процесса и оборудования. Получающаяся система уравнений включает обычно нелинейные интегро-дифференциальные и дифференциальные уравнения в частных производных.
Решение полученной системы требует задания начальных и граничных условий, а это возможно лишь при изучении элементарных актов процесса. Наличие математической модели с элементами теории надежности в общем случае позволяет с достаточной достоверностью перенести результаты лабораторных исследований вплоть до промышленных условий. Все вышеизложенное дает возможность своевременно получить исходный материал для расчетов с учетом внутренних связей и определить главные условия в технической реализации процесса.
За основу построения модели нами было взято уравнение скорости выхода годной продукции (производительности). В общем виде эта зависимость описывается следующим уравнением:
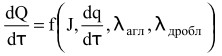(1)
где J - скорость зародышеобразования;
- скорость роста кристаллов;
λагл - скорость роста кристаллов за счет агломерации;
λдробл - скорость дробления кристаллов.
В понятие надежности процесса кристаллизации и работы кристаллизационного оборудования кроме стабильной производительности необходимо включить также и такие показатели: 1. определенное процентное содержание требуемого грансостава кристаллического продукта, 2. определенная чистота продукта, иначе минимальный процент примесей, 3. оптимальные (и даже min) расходы электроэнергии, тепла, холода, растворителя и т.д.
Скорость зародышеобразования - величина весьма сложная и зависящая более чем от десятка факторов. На нее оказывают влияние физико-химические свойства вещества и растворителя, параметры процесса, режим работы установки и ее конструктивные особенности.
Скорость зародышеобразования можно описать двумя зависимостями аналитической (2) и функциональной (3)
J = K (C-C0)m (2)
где К, m - постоянные. зависящие от физико-химических свойств растворенного вещества и растворителя, например, таких как произведение валентностей ионов вещества, число молекул кристаллогидратной воды, тип кристаллической решетки и т.д.;
С0 - абсолютная растворимость вещества, или концентрация пересыщенного раствора для данных условий;
С - действительная концентрация вещества в пересыщенном растворе.
(3)
где Пс = С - Со = f (C, Со) - величина пересыщения,
Пt = (tнас - tд) = f (tнас ,tд) -величина переохлаждения,
tнас - температура насыщения раствора;
tд - действительная температура при данном пересыщении (температура раствора);
Пc (φ) = f (tр, Со, Пвал., Мквg ,КР) - устойчивость пересыщения;
tp - температурный коэффициент растворимости;
Пвал - произведение валентностей ионов составляющих соль;
Мквg - число молекул кристаллогидратной воды;
КР - тип кристаллической решетки;
t0C = tд - температура раствора;
Θпр - количество и физико-химические свойства примесей, снижающих качество продукта, а, следовательно, влияющих на надежность процесса;
Vпер - скорость перемешивания.
Скорость роста кристаллов является функцией устойчивости пересыщения, скорости перемешивания раствора и его температуры, скорости инкрустации, если она имеет место, а также количества и свойств примесей.
Скорость роста кристаллов описывается в общем виде следующей зависимостью:
(4)
От величины устойчивости пересыщения будет зависеть форма образующихся кристаллов Фк, которая является одним из показателей качества получаемого продукта.
Скорость перемешивания Vпер раствора как один из параметров процесса кристаллизации, влияет на скорость диффузии вещества из раствора к граням кристалла Д, а это, в свою очередь, влияет как на скорость роста, так и на форму кристаллов.
Л.А. Разумовский использует в своей работе [2] для описания кинетики роста среднего кристалла следующее уравнение:
(5)
где А - коэффициент времени, определяемый режимом работы кристаллизатора. Следовательно, можно считать, что коэффициент А в определенной мере характеризует надежность процесса кристаллизации.
Взаимосвязь 
определяет основное условие надежности процесса по показателю «размер кристалла».
Согласно выводам Л.А. Разумовского [2] уравнение 5 в координатах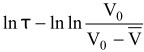 
дает прямую линию, k = 3 и не зависит от режима работы кристаллизатора. Итак, один из показателей надежности процесса кристаллизации и работы кристаллизационного оборудования можно всегда поддерживать на должном уровне, зная время роста кристаллов до требующегося размера.
В непосредственной близости от стенки аппарата (кристаллизатора, кристаллорастителя, трубопроводов) основной процесс идет несколько иначе (медленнее), а это позволяет побочным процессам развиваться быстрее. Этим и обусловливается процесс инкрустации, который снижает надежность основного процесса кристаллизации, т.е. замедляет скорость роста кристаллов, изменяет их форму, увеличивает наличие примесей в готовом продукте (товарных кристаллах), вследствие перехода полезной части раствора в инкрустационный слой и т.п.
Уравнение, описывающее процесс инкрустации, запишется в виде функциональной зависимости:
Fинкр = f (Пt ,Vпер ,Qпр ,Ст.ф ) (6)
где Ст.ф - комплекс величин, которые определяют пристеночный эффект.
Ст.ф = φ (Δt, x, ξ) (7)
Величина Ст.ф должна непосредственно отражать теплопроводность через слой l (пристеночаая зона), в котором проходит инкрустация.
Δt - градиент температур в пристеночной зоне;
х - координата фронта охлаждения;
ξ - положение границы раздела фаз;
δ - толщина стенки;
tд > tвоздуха; t0С = tж = t2; tст = tт = t1
Класс задач, связанный с фазовыми превращениями с выделением тепла или его поглощением (это характерно для процесса ивкрустации), относится к типу задач Стефана. Такая задача формулируется как задача о сопряженности температурных полей двух фаз (1 - твердой, 2 - жидкой) при наличии особого граничного условия на движущейся границе раздела фаз (уравнения 12, 13). Решение приведенной задачи (8 - 13) в данной математической постановке предложено В.Т. Меламедом [1], который учитывал теплоту фазовых превращений в виде непрерывно распределенных на фронте кристаллизации источников тепла. Это особый метод решения, т.к. условие на границе фаз (8, 9) относит задачу Стефана к классу нелинейных и решить её обычный путем не представляется возможным. Уравнение теплопроводности:
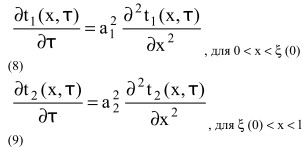
Дополнительные условия:
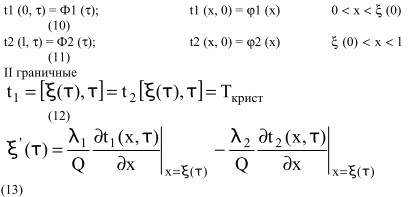
где а1, а2 - температуропроводность соответственно твердого и жидкого слоев;
λ- теплопроводность;
Q - количество теплоты кристаллизации в 1 м3;
т - время кристаллизации.
В функциональной зависимости (1) одним из аргументов роста кристаллов является λагл, т.е. параллельно основному процессу - росту кристаллов, увеличение их размеров может происходить еще за счет агломерации кристаллов.
Агрегированию могут подвергаться как зародыши, так и кристаллы любых размеров, разница лишь в том, что скорость агрегирования будет зависеть, в частности, от размеров контактируемых элементов.
В общем виде скорость процесса агломерации можно выразить следующим уравнением:
(14)
где Ипер - интенсивность перемешивания;
т - время кристаллизации (среднее время пребывания кристалла в слое);
Vt - скорость охлаждения раствора;
dо, V - размер (средний диаметр, объем) соответственно зародыша и кристалла;
σ - поверхностные силы натяжения;
Скр - концентрация кристаллов в слое.
На скорость роста кристаллов будет оказывать нежелательное воздействие дробление кристаллов, которое будет зависеть в общем виде от следующих величин:
λдробл = f (Vпер , Vt , V, Скр ,T) (15)
Рассматривать дробление по отношению к качеству продукта, как процесс уравновешивающий агломерацию, нельзя, вследствие того, что образующиеся осколки, как и образующиеся агломераты, снижают качество готового продукта, увеличивая неоднородность размеров.
Итак, анализируя уравнение скорости выхода годной продукции (1) можно установить следующее:
- Не все величины, входящие в это уравнение, оказывают положительное воздействие на процесс кристаллоращения и степень их влияния не одинакова.
- Такие факторы, как наличие примесей Qпр, протекание процессов дробления λдр и инкрустации Fинкр оказывают полное отрицательное воздействие на основной процесс, то есть снижают его надежность пропорционально величинам Qпр, λдр, Fинкр.
- Такие параметры, как Мквд, t°С, Vпер, т, Скр и процесс агломерации Хагл, могут оказывать нежелательное воздействие на основной процесс, если не поддерживать их на оптимальном уровне.
Литература.
- Меламед В.Т. Сведение задачи Стефана к системе обыкновенных дифференциальных уравнений. Известия АН СССР. Серия геофизика, 1958. № 7.
- Разумовский Л.А. Исследование кинетики процесса кристаллизации солей из растворов во взвешенном слое. 1967. Кандидатская диссертация. г. Иваново. ИХТИ.