При решении прикладных задач необходимо по набору экспериментальных данных, содержащих систематические и случайные ошибки, выбрать такую математическую модель, которая наиболее адекватно описывает исследуемое явление или процесс. Если изучаемый объект описывается линейной по параметрам функцией вида
y = F(x, a), (1)
то необходимо определить точечные и интервальные оценки параметров, а этой функции. Пусть ошибка измерения в каждом опыте составляет εi , то тогда истинные значения параметров функции (1) а* должны удовлетворять системе неравенств:
(2)
В работе [1, 2, 3] показано, что область Ω возможных значений параметров а при интервальной ошибке измерения представляет собой выпуклый многогранник.
В качестве точечной ошибки параметров можно использовать либо геометрический центр множества неопределенности, либо решение экстремальной задачи вида
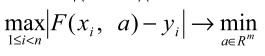(3)
При практическом использовании метода центра неопределенности [МЦН] представляют интерес аппроксимации множества Ω простыми геометрическими фигурами сверху и снизу. В качестве таких фигур использовали прямоугольник и эллипс. В этом случае точечной оценкой параметров может служить геометрический центр выбранных фигур. Необходимо подчеркнуть, что разработанные алгоритмы обладают свойством рекуррентности, что позволяет по мере поступления информации об изучаемом объекте последовательно уточнять точечные оценки и уменьшать интервальные оценки.
В данной работе приведены результаты расчетов начальной концентрации исходного вещества и констант скорости реакции обратимой
g реакции первого порядка превращения γ-оксимасляной кислоты в соответствующей ланктон и воду [4]. В таблице 1 приведены исходные кинетические параметры этой реакции.
Таблица 1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
А(i) моль/л |
0.1582 |
0.1450 |
0.1324 |
0.1213 |
0.1115 |
0.1012 |
0.0923 |
0.0788 |
0.0668 |
|
ti, мин |
21 |
36 |
50 |
65 |
80 |
100 |
120 |
160 |
220 |
При проведении вычислительных экспериментов оценки погрешности измерений текущих концентраций вещества и времени варьировали в широких пределах. В таблице 2 приведены результаты расчетов параметров a, b линейной зависимости y = a + bx, где b = -(k1 + k2). Значение начальной концентрации определили по формуле 
где 
= 0,0495 моль/л - точное значение концентрации γ- оксимасляной кислоты. Расчеты проводили по методикам прямоугольника в МЦН, рекуррентного прямоугольника в МЦН (для двух случаев: при точном измерении входной переменной ti и неточном измерении входной переменной ti), взвешенного эллипса неопределенности в МЦН. Данные методики описаны в [5-7].
Таблица 2
 |
|
A0 |
Размеры области неопределенности |
Метод |
|
2.016872 |
0.009414 |
0.1827896 |
1,34 • 10-7 |
Прямоугольник в МЦН |
|
2.038648 |
0.009217 |
0.182355 |
1,42 10-7 |
Рекуррентный прямоугольник в МЦН |
|
2.01807 |
0.00940 |
0.18241 |
1 • 10-7 |
Взвешенный эллипс в МЦН |
|
2.027299 |
0.009306 |
0.018119 |
4,17 • 10-7 |
МНК |
Непосредственно из экспериментов получены значения параметров: b = 0,0094, (-а) = 2,01807, которому соответствует начальная концентрация γ -оксимасляной кислоты А0 = 0,18241 моль/л. Таким образом
оценки параметров, полученные по предложенным методикам практически совпадают с экспериментальным значениям. Все расчеты выполнены по программе «Аппроксимация экспериментальных данных».
СПИСОК ЛИТЕРАТУРЫ
- Вощинин А.П. Решение задач оптимизации по интервальным оценкам критерия // Зав. лаб. - 1987. - Т.53, № 7. С. 45-48.
- Вощинин А.П., Дывак Н.П. Планирование оптимального насыщенного эксперимента в задачах анализа интервальных данных // Завод. Лаб. - 1991. - Т.57, № 7. - С. 56-59.
- Вощинин А.П. Метод анализа данных с интервальными ошибками в задачах проверки гипотез и оценивания параметров неявных линейно-параметризованных функций // Завод. лаб.-2000.- Т.66, №3. - С. 51-65.
- Эмануэль Н.М., Кнорре Д.Г. Курс химической кинетики. М.: Высш. шк., 1984. - 463 с.
- Белов В.М., Гончаров С.А., Пролубников В.И., Унгер Ф.Г., Лукьянцева М.В. Алгоритмы прямоугольника в методе центра неопределенности для оценивания параметров линейных функций. -Томск, 2001. - 36 с. /Препринт ТНЦ СО РАН/.
- Белов В.М., Евстигнеев В.В., Суханов В.А., Лагуткина Е.В. Интервальная кинетика химических реакций. Методика взвешенного эллипса неопределенности в кинетике обратимых реакций первого порядка // Изв. вузов. Химия и хим. технология. - 1999. - Т.42, № 1.- С. 41 - 45.
- Белов В.М., Гончаров С.А., Гончарова Н.Л. Рекуррентный алгоритм оценивания параметров линейной двухпараметрической функции // Междунар. конференции «Физико-химические процессы в неорганических материалах», Ч.2. - Кемерово: Кузбасвузиздат, 2001. - С. 134-135.