Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Введение

Для функционального описания поведения территории нами вводятся новые понятия - активность и интенсивность растительного покрова. Причем территория понимается как простейшее геодезическое изображение ландшафта. А сам ландшафт, в свою очередь, является первым компонентом динамической геотриады «ландшафт + население + хозяйство».

Активность учитывается по доле площади растительного покрова (леса и древесно-кустарниковая растительность, луга и пастбища, особо охраняемые территории и болота) и этот экологический параметр позволяет характеризовать фактически образовавшиеся отклонения от территориального экологического равновесия [1] на конкретной территории.

Однако пока отсутствуют данные земельных кадастров по конкретным землепользователям. Поэтому приведены значения параметров растительного покрова по административным районам и городам субъекта федерации. В частности рассмотрены районы и города Республики Марий Эл (РМЭ) по состоянию распределения земель на 01.01.07 г.

В наиболее общем случае интенсивность проявляется как активность во времени. Физически интенсивность - это скорость изменений. А активность - это сами изменения в природной, природно‒техногенной или технической среде (по площади, урожайности растений, продуктивности почвы и пр.) в некотором срезе времени.

Ритмика жизнедеятельности растений четко предопределена циклами вращения Земли вокруг Солнца, поэтому единицей измерения любого показателя (параметр - это показатель, характеризующий исследуемую систему) растительного покрова и его компонент станет год. Активность и интенсивность поведения человека по отношению к процессу уничтожения ландшафта быстротечны. Например, планировалось атомными взрывами построить русло крупного канала для переброски воды северных рек на юг.

Растительный покров - это территориально распластанное живое существо, обладающее многими свойствами поведения живого вещества. Индикатором экологического равновесия на данной территории становится его активность. Она в простейшем случае исчисляется по доле занятой площади, причем в ходе конкуренции за плодородные почвы, с человеком. А интенсивность поведения (скорость реакции на внешние раздражения, в том числе и на антропогенные воздействия) растительного покрова за более чем 350‒450 млн. лет эволюции наземных растений пока не изменилась. За скоростью эволюции человека растения явно не успевают. Но они это возместят высокой своей активностью роста и развития сорняков, а также ликвидацией нужных человеку видов культур болезнями.

Травяной покров. Особое место в растительном покрове занимает травяной покров, и он более живуч, устойчив и стабилен в своем поведении по сравнению с древесными пологами. По данным американских ученых, трава появилась около 100 млн. лет назад. А деревья возникли 350‒450 млн. лет назад, то есть трава появилась как результат отклика древесных растений на поведение наземных животных. Поэтому трава биологически устойчивее деревьев, кустарников и кустарничков. При снижении плодородия почвы и ухудшении климата деревья исчезают, а их место обитания занимают степные травы.

Интенсивность воспроизводства травяного покрова. Годичная цикличность определяет урожайность травы в естественных условиях роста и развития, какими являются естественные луга, на которых заготовляется сено. Улучшенные луга уже меняют свое поведение, повышая урожайность на позитивное воздействие человека культурными и техническими мерами и внесением на такие луга удобрений.

Из статистического сборника [6, с. 181] были взяты сводные данные по сенокосным лугам Республики Марий Эл (РМЭ), приведенные в таблице 1.

Таблица 1

Урожайность сена в сельских хозяйствах на территории РМЭ, ц/га 

Примечание: * Недостатком динамического ряда является отсутствие данных по всем годам в промежутках между пятилетками, что не позволяет точно выявить циклы с полупериодом менее пяти лет.

Вначале рассмотрим статистические закономерности динамики урожайности травы после естественной сушки в сено на сенокосных лугах сельских хозяйств всех категорий. При этом будем выполнять все этапы статистического моделирования:

‒ эвристическая идентификация, когда выясняется логика каждого динамического ряда исходных количественных данных;

‒ структурная идентификация, когда по эвристической модели понимание процессов изменения значений изучаемого показателя выбирается основная (естественная составляющая) закономерность, то есть тренд изменения во времени исследуемого показателя;

‒ параметрическая идентификация, когда в решающей математической среде типа CurveExpert‒1.3 подбираются значения параметров статистической модели исходной конструкции, полученной на предыдущем этапе структурной идентификации.

После выполнения всех процедур и этапов идентификации биотехнического закона, предложенного проф. П.М. Мазуркиным [2‒5], сформируется готовая статистическая модель. Урожайность сена с естественных и улучшенных сенокосов со всей площади по РМЭ определяется рядом значений по точечному графику на рис. 1.

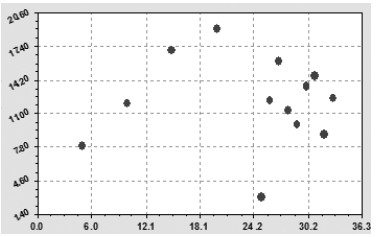
Рис. 1. Изменение урожайности сена естественных и улучшенных сенокосов

Республики Марий Эл, ц/га

Из роя точек резко выделяется одна (самая нижняя) точка.

Полнота динамического ряда. Пусть исходные данные [6, с.181] количественно достоверны и статистики адекватно описали табличными моделями типа табл. 1 картину динамики исследуемого явления или процесса. Тогда можно поставить задачу оценки полноты статистического ряда динамики значений изучаемого показателя.

Критерий полноты значений показателя. Представим динамический ряд значений урожайности сена с естественных и улучшенных сенокосов со всей площади по РМЭ в виде последовательности, показанной в таблице 2.

Весь этот ряд динамики можно разделить на две части:

а) динамика по пятилетним циклам, причем четко по хронологическому времени 1970, 1975, 1980 и т.д.;

б) динамика по годичным циклам, что соответствует действительности, то есть ритму вращения Земли вокруг Солнца.

Таблица 2

Полный динамический ряд урожайности сена, ц/га 

Введем новый показатель оценки добротности статистических данных динамического ряда - это коэффициент полноты ряда. Этот коэффициент k будет вычисляться как отношение количества m имеющихся значений показателя в ряду к общему количеству возможных членов n динамического ряда, то есть по формуле k=m/n .

Из данных табл. 2 получаем m=14 и n=34. Поэтому коэффициент полноты ряда будет k=14/34=0,412. Динамический ряд оказался сильно деформированным. Специальными уловками группировки исходных данных вовсю занимались советские экономисты, чтобы доказывать недоказуемое. Нужно статистическим службам запретить публикации неполных динамических рядов, так как это почти всегда приводит к ложной идентификации.

Картина распределения точек, показанная роем на рисунке 1, оказалась ложной из-за отсутствия 20 точек из требуемых 34 значений изучаемого показателя. При этом не ясно, какими по расположению относительно принятой системы координат были точки в промежутках между пятилетками. Поэтому может оказаться, что полный статистический ряд даст совершенно иную модель динамики (если урожайности 1970, 1975, 1980, 1985, 1990, 1995 годов окажутся не максимальными, а иными). Вот почему надо обращать серьезное внимание на полноту статистического ряда динамики значений изучаемого показателя.

Границы доверительного интервала статистического ряда. Применим известный прием выделения верхней и нижней границ доверительного интервала. Это обезопасит от ложной идентификации и неправильной трактовки найденной формулы, так как верхняя и нижняя границы показывают только возможное поле распределения значений показателя вне зависимости от полноты статистического ряда.

Перепишем первую часть показателей таблицы 1 с учетом границ доверительного интервала и результаты приведем в таблице 3.

Верхняя граница урожайности сена естественных и улучшенных сенокосов определится уравнением (рис. 2) вида

q_max=14,5092exp(-0,0091099t)+4,7361×10^-8t^9,23434exp(-0,44353t). (1)

Максимальная относительная погрешность уравнения (1) равна 4,59 %. Коэффициент корреляции по рис. 2 равен 0,9861.

Нижняя граница урожайности сена (рис. 3) определится статистическим уравнением

q_min = 7.64985exp(-0,0052882t)+0,000403119 t ^5,45669 exp(-0,31879t). (2)

Максимальная относительная погрешность уравнения (2) равна 3,84 %, а коэффициент корреляции по рисунку 3 равен 1,0000, то есть формула (2) становится однозначно функциональной математической зависимостью.

Таблица 3

Урожайность сена в сельских хозяйствах всех категорий на территории РМЭ, ц/га 

Примечание: * Такие резко отклоняющиеся точки исключаются из статистических рядов. 

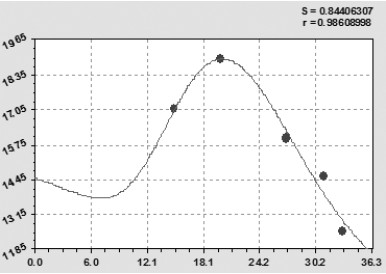
Рис. 2. Верхняя граница доверительного интервала урожайности сена естественных

и улучшенных сенокосов РМЭ, ц/га

Закономерности динамики урожайности сена. Конструкция уравнений для описания верхней и нижней границы доверительного интервал одинакова. Она содержит две составляющие:

а) закон гибели (спада) в упрощенной конструктивной форме, когда третий параметр статистической модели будет равен единице;

б) биотехнический закон проф. П.М. Мазуркина [2‒5] в упрощенной форме (когда четвертый параметр модели равен единице).

Когда известна общая конструкция статистической закономерности, то можем её применить ко всему динамическому ряду новых исходных статистических данных.

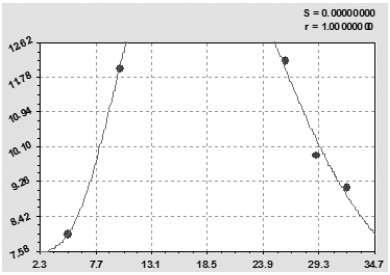
Рис. 3. Нижняя граница доверительного интервала урожайности сена естественных и улучшенных сенокосов РМЭ, ц/га

В результате идентификации был получен тренд (рис. 4) из двух составляющих в виде устойчивых законов, в котором знак экспоненциального закона изменился с отрицательного на положительный, и он стал показывать рост значений урожайности сена. При этом 1995 год не был исключен.

q=10,9017exp(0,00083530t)+1,1128×10^-10 t ^14,0597 exp(-0,88382t), (4)

После исключения резко отклоняющейся от других значений показателя точки, отмеченной в данных табл. 3 звёздочкой, была получена формула (рис. 5) статистической закономерности вида

q=11,4401exp(-0,0010562t)+4,9549×10^-12 t ^14,74586 exp(-0,80755t). (5)

Коэффициент корреляции увеличился до 0,7266, а закономерность стала одинаковой с границами доверительного интервала.

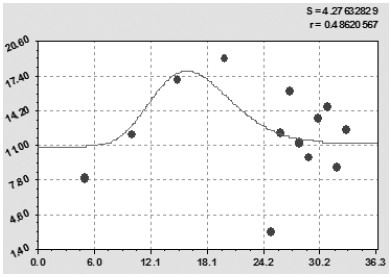
Рис. 4. Тренд урожайности сена естественных и улучшенных сенокосов РМЭ, ц/га

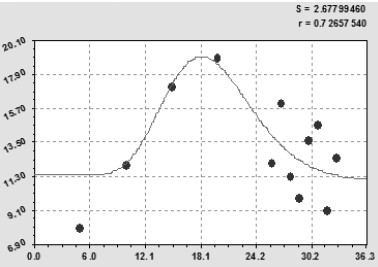
Рис. 5. Тренд урожайности сена естественных и улучшенных сенокосов РМЭ после исключения резко отклоняющейся точки, ц/га

При этом попытка наращивания первой составляющей до закона гибели в полной форме не дает результата. Остатки приведены на рис. 6.

Чередование знаков остатков ε показывает, что можно дополнить составляющей в виде закона колебательного движения.

Структурно-параметрическая идентификация выполняется относительно вейвлет‒функции проф. П.М. Мазуркина [2‒5] вида

q₃ = Acos(πt/p0.5±a10), (6)

где A - амплитуда (половина) колебательного движения значений изучаемого показателя во времени по биотехническому закону

(6а)

p0.5 - половина периода колебательного возмущения показателя по биотехническому закону (с учетом предыстории в виде постоянного члена)

, (6б)

a1...a10- параметры исходной конструкции статистической модели (6), являющейся обобщенным законом колебательного изменения значений изучаемого показателя.

Волновую закономерность нельзя искать по статистическим выборкам с пропусками данных. Поэтому принимается интервал времени с 1995 по 2003 гг. (причем результат 1995 года исключается).

После нескольких сеансов поиска значений параметров модели (6) в математической среде CurveExpert‒1.3 была получена конкретная закономерность в виде сложного уравнения

q=5,64537exp(0,022908t)+6,0178×10^-13 t ^14,8210 exp(-0,74130t)-A₁cos(πt/p₁+3,29024)+

+A₂cos(πt/p₂+1,31367), (7)

A₁ = 2,09541 t ^0,15870 exp(-0,0037692t), p₁ = 2,79259 - 0,019856t,

A₂ = 4,1925×10^-9 t ^8,82490 exp(-0,38095t), p₂ = 1,12563 + 0,00014490t.

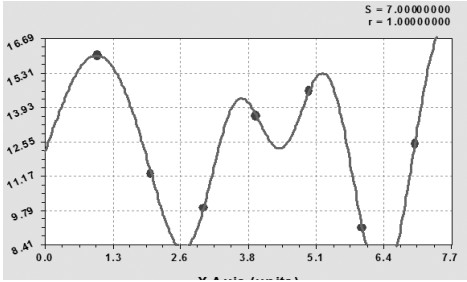
Рис. 7. Динамика урожайности сена естественных и улучшенных сенокосов РМЭ за период 1970‒2003 гг., ц/га

В статистической модели (7) из четырех составляющих две последние являются колебательными возмущениями. Из-за отрицательного знака первая волновая зависимость является кризисным возмущением сенокосных лугов на внешние раздражители (естественные и антропогенные), причем частота возмущения растет, а вторая волна с начальным периодом в 2×1,12563 = 2,25 лет показывает позитивное успокоение травяного покрова со снижением частоты адаптивного возмущения.

Сокращение ряда до 1996‒2003 гг. сужает прогнозные возможности готовой статистической модели. Исходя из высокой точности, когда максимальная относительная погрешность равна всего 0,47 %, уравнение (7) дает возможность принять горизонт прогноза, равный основанию прогноза, то есть в восемь лет до

2003 + 8 = 2011 года.

А при ряде со всеми 34 точками получили бы возможность прогноза до

2003 + 34 = 2037 года.

При этом остатки располагаются так, как это показано на рис. 8.

Расположение остатков показывает, что существует еще одна волновая составляющая с примерным периодом в пять лет. Погрешность измерений урожайности сена недостаточно высока, чтобы искать вейвлет‒функцию с амплитудой менее 0,08 ц/га (запись в справочнике [6, с.181] выполнена с округлением до одной десятой, поэтому точность измерений составляет ±0,05 ц/га).

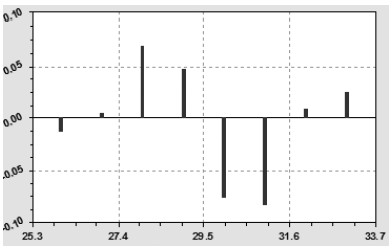
Рис. 8. Остатки готовой статистической модели тренда (4.11) урожайности сена естественных и улучшенных сенокосов РМЭ, ц/га

Изменение шкалы времени. Если исключить пятилетние данные, а также резко отклоняющуюся точку 1995 г., то получим динамический ряд с новой шкалой абсцисс. Переход выполняется по формуле t₁=t‒26.

Для новой шкалы получаем условие t₁ = 0 для 1996 года. Такое сокращение времени приводит и к уменьшению количества составляющих модели.

После повторной параметрической идентификации модели (4.11) была получена формула (рис. 9) с тремя составляющими

q=12,3327exp(-0,00036540t) -A₁cos(πt/p₁+1,53433)+A₂cos(πt/p₂ -2,93294), (8)

A₁ = 3,63948exp(0,0089534t), p₁ = 1,91645-0,028705t,

A₂ = 0,034478 t ^8,51786 exp(-1,80140t), p₂ = 1,16822 - 0,0086746t

Рис. 9. Динамика урожайности сена естественных и улучшенных сенокосов РМЭ за период 1996‒2003 гг., ц/га

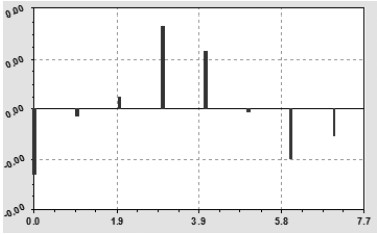
Рис. 10. Остатки готовой статистической модели тренда (4.12) урожайности сена естественных и улучшенных сенокосов РМЭ за период 1996‒2003 гг., ц/га

По коэффициенту корреляции 1,000 и нулевым остаткам (рис. 10) модель (8) стала однозначной.

Даже по малым остаткам, находящихся в интервале пренебрежимо малых для практики измерения массы сена чисел ǀɛǀ=7·10^-12...7·10^-10 на рис. 10 наблюдается новая волновая закономерность. Этот факт означает, что повышение точности измерения массы травы и сена с единицы площади позволит находить статистические закономерности динамики урожайности.

Список литературы

1. Реймерс, Н.Ф. Природопользование: Словарь‒справочник / Н.Ф. Реймерс. - М.: Мысль, 1990. - 637 с.
2. Мазуркин, П.М. Геоэкология: Закономерности современного естествознания: Научное изд. / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с.
3. Мазуркин, П.М. Закономерности устойчивого развития / П.М. Мазуркин. ‒ Научное издание. - Йошкар-Ола: МарГТУ, 2002. - 302 с.
4. Мазуркин, П.М. Рациональное природопользование: учебное пособие. В 3‒х ч. Ч. 1: Экологически ответственное землепользование / П.М. Мазуркин, С.Е. Анисимов, С.И. Михайлова; под ред. П.М. Мазуркина. - Йошкар-Ола: МарГТУ, 2006. - 176 с.
5. Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МарГТУ, 2006. - 292 с.
6. Республика Марий Эл: Статистический ежегодник / А.В. Целищев и др. - Часть 1. - Йошкар-Ола: ФСГС, 2004. - 342 с.

Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603 МОН РФ