I. ФИЗИЧЕСКАЯ ТЕОРИЯ
Определение 1. Мультипликативной квазигруппой называется объект Q = {M, S, P}, где M - множество, S - сигнатура, операция умножения в которой неассоциативна, Р - правила вывода (включающие аксиоматику). Q имеет единицу и обратный элемент.
Пример 1: Березниковская квазигруппа B ([2], см. список литературы в Части 2).
Определение 2. Квазимоноидом называется объект Q = {M, S, P}, где S не содержит операции деления (нет обратного элемента).
Постулат 1: Объект Q ≡ Q(F) = Q
F, где F - множество непрерывных функций, является математической основой соответствующей физической теории Ф ≡ Ф(Q).
Постулат 2: Действие системы операторов G над Q генерирует систему уравнений движения и состояний физики Ф ≡ Ф(G, Q).
Постулат 3: Существует отображение φ: GQ →Ф(Rn), где n = dim Q.
В общем виде модель физики Ф = {Q, G, I}, где I - система интерпретации, включающая содержательное обоснование, и М - предметное множество. В случае D C G, где D - множество дифференциальных операторов, получим подмножество дифференциальных моделей физики Фd C Ф.
Ближайшим к ассоциативным алгебрам объектом Q является альтернативная алгебра октав О. Она нормирована и над полем Р действительных чисел R образует октетное пространство О, над которым действует G, включающая множество дифференцируемых функций Fd C F и дифференциальных операторов D.
Пример 2. Пусть 
-
где jn - единицы алгебры октав, Un - n-я переменная на множестве дифференцируемых реальных функций от вещественных компонент zn октетной переменной z = z0 + j1z1 + ... + j7z7, zn R. Выражение U = uT + ix + jy + kz + m´(αH + ipx + jpy + kpz)E, где u - константа размерности (характерная скорость, u = c - постоянная Лобачевского), T = T(t, x, y, z, px, py, pz) - физическая длительность, или провремя, t - параметрическое (евклидово) время, x, y, z - параметрические пространственные координаты (материальной точки), m´ - константа связи между кватернионами размерности кг/c, - постоянная размерности, H = H(t, x, y, z, px, py, pz) - энергия (функция Гамильтона), px, py, pz - импульсные координаты (материальной точки), а единицы jn переобозначены согласно законам умножения в О, называется предметным термом. Выражение, представляющее собой обобщение дифференциального оператора Гамильтона на восемь целочисленных измерений, Û = δ/u δt + i δ/ δx + j δ/ δy + k δ/ δz + m´( βНC + i δ/ δpx + j δ/ δpy + kδ / δpz)E, где β - константа размерности, НC- оператор, аналогичный гамильтониану (в квантовой механике), - называется операторным термом октетной физики. Произведение образующих: ÛU называется ядром октетной физики.
Тогда для U / I имеет место:
Основная теорема: Статичность гиперсферы U 2 = R 2 в пространстве О является условием существования уравнений движения в R8
Действительно, 
=0 и ввиду альтернативности умножения отсюда следует U(d/dz)U=0.Умножая последнее уравнение слева на U и сокращая на R2, придем к равенству (d/dz)U=0. Полученные восемь уравнений после сокращения гиперкомплексных единиц – вещественные: одно уравнение – для провремени Т, три уравнения – для компонент радиуса-вектора, одно уравнение – для энергии итри уравнения – для компонент импульса (см. ниже). Тем самым произведено конкретное отображение φ:D O(F)→Ф (R8).
Приложения и следствия теоремы – в [1 – 5], см. список литературы в Части 2.
Следствие 1: В О основная теорема является обобщением классического принципа наименьшего действия (см. в [1]); в общем случае условие (d/dz)U = 0 может включать ортогональные к подпространствам О Zn террасы по условию {δ/δzn,δ2/δzn2}=0 и седловые точки.
Общая теорема: Экстремум функционала 
в области О © О, где k € N, ak, a0, U € O, указывает на условия существования неисчислимого множества физических вселенных, основной закон движения в которых определяется обобщенным принципом экстремального действия: df(U)/dz = 0. Действительно, получаем: 
откуда, поскольку аq произвольны и U ≠0, следует d/dz U =0 , где оператор 
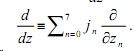
Основная теорема является частным случаем общей теоремы, справедливой для неассоциативных функций.
Вывод о многолистности Фd (О) получен в [2]. Вывод о существовании неисчислимого множества физических вселенных равносилен выводу о самоограниченности численных мето- дов вообще и геометрических методов в частности (вырождение физической картины мира по f(U) неустранимо в рамках количественных подходов – это «прообраз» калибровочных условий).
Экстремум (плюс седловые точки и террасы) функционала f(U) означает устойчивость поло- жения альтернативного наблюдателя U2 относительно «внешнего» |U| > R и «внутреннего» |U| < R миров (гиперкомплексных миров). В «предельной» геометрии выявляется ограниченность Эрлангенской программы геометризации физики. Содержательные основания и аксиоматика октетной физики О ≡ Фd(O) из класса Фd(Q) для линейных дифференциальных операторов 1-го порядка рассмотрены в [1, 3, 4, 13]. Таблица умножения биоктетной алгебры 2O, являющейся квазимоноидом, приведена в [3]. Биоктетная механика представлена в [4]. Таким об- разом, предложен метод дедуктивного по- строения физических теорий.
Физика называется черно-белой, если она строится на основе моделирования физического пространства-времени геометрией Минковского или римановым пространством (2 единицы коммутативного и ассоциативного поля комплексных чисел: 1 и i). Физика называется цветной, если она строится на основе моделирования физического пространства-времени октетным пространством, другими квазигруппами и/или квазимоноидами размерности dim > 8 (8 и более единиц неассоциативных тел).
Обобщенной механикой называется значение ядра системной физики в точке экстремума: d/dzU=0 , где z и U – предметные термы, включающие обобщенные механические координаты (аргументы: время, пространственные и импульсные координаты, энергия, координаты момента импульса и момента силы и т.д.).
1.1. ОКТЕТНАЯ ФИЗИКА
Запишем систему дифференциальных уравнений октетной физики (1994, см. [3, 13]):
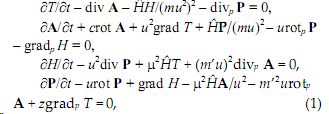
где t – параметрическое время, вводимое априорно; Т – генератор физической длительности, провремя; А – вектор физических координат; Р – вектор физического импульса; Н – функция, подобная гамильтоновой; Ĥ – аналог гамильтониана; u – характерная скорость (при u = с – первая постоянная Лобачевского); μ = m’/m; z = (m’u) 2 ; m’ – новая константа размерности кг/с; m – масса тела (системы тел); gradp, rotp, divp – операторы по импульсным координатам. Аналогично строится октетная электродинамика с отличным от нуля зарядом магнитного монополя [3]. Элементарный интервал в случае изменения (измерения) отсчетов времени в О имеет вид:
где константы размерности для краткости опущены, v – относительная скорость систем отсчета S и S’, f – сила (плотность силы), действующая на систему (в системе) S, w – мощность (плотность мощности), выделяемая (поглощаемая) в системе (системой) S. Отсюда вытекает, что время и пространство зависят не только от относительной скорости движения систем отсчета S и S´, но и от процессов энергообмена и силового взаимодействия между телами, составляющими эти системы отсчета (систему S).
Ввиду абсолютности силовых характеристик реального физического движения и сил инерции в формулах преобразований элементарного интервала ds € O снимается скоростной релятивизм СТО. Численные решения системы (1) при некоторых условиях на Т и
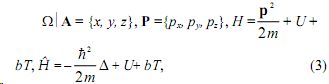
где h – постоянная Планка, Δ – оператор Лапласа, U – силовая функция (принимаем U = – α/r, а в общем случае при сохранении вида первых слагаемых в Н и Ĥ функция U – восьмая неизвестная функция в системе (1)), b – числовой коэффициент, приводят к множеству новых эффектов.
Решение (1) для звездного шара ([5] и см. ниже) привело к теоретическому обнаружению двух новых характерных скоростей: u = 7.9904. 1017 см/c – определена из условия однозначности в узле графа состояний, отвечает гравитационному взаимодействию; v = 4.8875. 1035 см/c – определена непосредственно из топологии решений, отвечает генерации инертной массы и пространственных отношений.
Логические возможности существования тахионов рассмотрел Ю.Б. Молчанов [7]. Другие результаты: 1) эффект «тюльпан» [3] как альтернатива бесконечному гравитационному коллапсу; 2) обнаружение нестандартной памяти пространственной субстанции, отличной от памяти инерции [3]; 3) обнаружение гипермасштабных пульсаций Метагалактики и ее автосолитонной структуры [2]; 4) теоретическое обнаружение ядра электрона [2]; 5) объяснение феномена квантовых неопределенностей квантовой механики (см. [1 – 3]); 6) эффект обтекания энергетического центра может быть исследован в Космосе (искривление лучей света Солнцем) и, возможно, использован для защиты от ударов быстрых механических объектов.
Положим в системе уравнений октетной физики (1) постоянную m’ = 0 и перейдем от векторов физических протяженности А и импульса Р к обобщенным координатам классической механики: xs, ps, где s = 1, 2, 3. Тогда получим систему уравнений пост’октетной механики (о решениях и расширении формализма см. [14, 15], Часть (2):
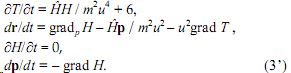
Если рассматривать (3’) на многообразии Т ≡ 0, то при условиях Ω получим квазиоктетную механику (о решениях и расширении формализма см. [14, 15], Часть 2):
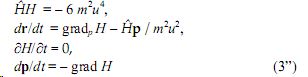
где u – характерная для конкретной задачи скорость, m – масса тела.
Октетная физика содержит тела многих известных теорий, среди которых классическая механика в формулировке Гамильтона – при А, Р из (3), Т = 0, μ ≡ 0, u →∞:
dr/dt = gradp H,
dp/dt = – grad H (4)
а также СТО (лоренц-инвариантность является частным случаем преобразований в октетном пространстве), равновесная термодинамика моногенной системы [2], электродинамика Максвелла [3], классическая квантовая механика [3]. Она переходит в формализмы этих и многих других новых теорий в предельных переходах, но не сводится к их простому объединению. Решения (3’), (3”) указывают на эфемерность флогистона массы в некоторых взаимодействиях.
1.2. БИОКТЕТНАЯ МЕХАНИКА
Использование алгебры 2О дает возможность моменты импульсов и сил рассматривать в едином подходе с обобщенными координатами октетной физики в варианте Ω. Это приводит к системе в работе [4], посвященной исследованию гравитации.
Выпишем уравнений биоктетной механики в соответствии с формализмом [6]:
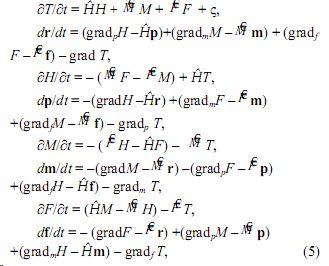
где М = {M, mx, my, mz} – 4-вектор M- момента импульса; F = {F, fx, fy, fz} – 4-вектор F- момента силы; gradю – оператор градиента по величине ю; Ю – оператор компоненты Ю в Ю, ς = 12 – показатель (синергетической) необрати- мости провремени Т (см. [9]). Mасса m, константы размерности и связи, среди которых могут быть постоянная Лобачевского с при u = c, по- стоянная октетной физики m´, характерные расстояние r0 и скорость v0, для краткости опущены. Остальные величины известны по уравнениям октетной физики.
Коэффициенты у операторов и функций в системе (5):
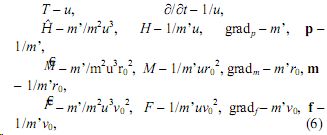
где r0, v0 – новые константы процессов. По смыслу задач возможны замены констант: v0 → r0ω0, v0 → r0 / t0. Результат исследований системы уравнений (5): пробное тело устремляется в сторону, противоположную направлению силы гравитационного притяжения – при определенных соотношениях момента импульса, момента силы и частоты их прецессии [4].
II. ОКТЕТНАЯ МЕХАНИКА В АСТРОФИЗИКЕ И КОСМОЛОГИИ
2.1. НЕГАМИЛЬТОНОВА МЕХАНИКА
Рассмотрим частный случай постгамильтоновой механики (определение в [13]). Из системы (3) в [3] при условиях для нерелятивистской по первому уравнению системы (4) в [3] и Т = 
, где α =GmгпMга, G – гравитационная постоянная, mгп – гравитационная пассивная масса, Mга – гравитационная активная масса, h(t) – зависимость от параметрического времени t, следующая как из симметрии Т и потенциала U = βr –n в Н, так и из симметрии Т и ε в предметном терме (добавка h(t) ~ bT), а также при условиях (*), см. выше: 
– придем к системе уравнений:
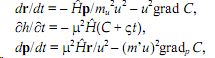
где μ = m΄/mи, m΄ – константа октетной физики размерности кг/c, mи – инертная масса проб ного тела, число ς = 6 – показатель асимметрии провремени Т (и р(T), f(T)) относительно отражения t → – t (этого нет в классической механике ввиду T≡ 0 и, далее, равенств p = mv и f = md 2 r/dt 2 ; в ней нет также асимметрии относи тельно отражения координат, т.е. классическая механика Р-четна, Т-четна и РТ-четна, если векторы p, v, f расположены в том же координатном пространстве, что и вектор r), u – константа нормировки размерности м/c, см. [3], С = С(x, y z, px, p y, pz) – постоянная интегрирования по первого уравнения системы (4) в [3].
Примем 
, где Δ- оператор Лапласа, r – расстояние между центрами (точечных) масс, 2πh – постоянная Планка. Если функция С состоит из линейной по коорди- натам и гармонической частей, то h(t) = hoexp[– μ2 (Ct + 3t 2 )] + α/r, где ho > 0 – постоянная интегрирования (в первом приближении h(t) = α/r + ho(1 – μ2 Ct)). Подставив h(t) в уравнения (1), получим систему:
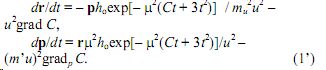
При t → ∞ первые члены справа исчезают, и система приобретает вид:
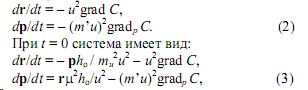
откуда при С ≡ 0 и р/mu = dr/dt получаем: ho ~ – mu u2 (или ho ~ |m u| u2 , см. ниже).
Из (2, 3) видно, что той феноменологической «гравитации», которую ввел в физику Ньютон, как и любой другой «гравитации», от момента рождения и до заката физической вселенной, вообще говоря, нет. Кроме того, при t ≈ 0, t ≈ ∞, а также в микро- и мегамире механика кардинально отличается от механики Гамильтона. То есть физический мир не ограничивается классиче- скими механиками, включая электромагнитизированную механику Эйнштейна (СТО) и квантовую механику. В сущности, механики (2) и (3) – принципиально новые теории.
Условия (*) могут выполняться в атто- и микромире, когда mu ~ 0, а также в масштабах Метагалактики, когда инертная масса объекта (звезды) много меньше массы Метагалактики. Поэтому можно принять, что первые члены справа в (1’) и (3) отвечают генерации материи и энергии (при соответствующих переменных в (2, 3) стоят символы |t =∞ | , |t = 0| ):
dr/dt = – pho /mu 2 u2 ,
dp/dt = rμ2 ho/u2 , (4)
Отсюда следует, что генерация материи и энергии описывается гармонической функцией с частотой ω= hom´/mи2u2 (в общем случае: ωn = nω ). Это значит, что все волновые явления в физической вселенной в интервале существования 0 < t <∞ являются отражением ее состояния на границах бытия, определенного принятием постулата октетного пространства, т.е. их причина
- в физике следующей октавы. Кроме того, т.к. генерация «данной в ощущениях» материи имеет волновой характер, то и разновидность гравитации, возникающая при нарушении условий (*), - явление гармоническое. Данный вывод подтверждается на опыте - в обнаруживаемой структуре Метагалактики [2], в которой превалируют вихри и соответствующие движения.
Поиски состояний Метагалактики (а тем более Вселенной) с помощью «уравнения Шредингера для Вселенной» лишены физического смысла и глубоко метафизичны.
Механика Гамильтона является своеобразным «зеркальным» отражением механики, выполнимой в моменты t ≈0, t ≈ ∞ , т.е. механики скрытой материи и энергии на ее «границах проявления». В макромире обычная механика в известных пределах точности остается приемлемой.
Вид функции h(t) указывает на то, что рождение материи экспоненциально замедляется. В области v C V3 перехода механики (1) в механику Гамильтона, как это следует из сравнения соответствующих систем уравнений, m´2 ≈- αmи/rv3, где rv € v. Отсюда вытекает, что если v существует и |m u| = mгп , то mu < 0 и в приближении закона тяготения Ньютона физический смысл постоянной m’ состоит в рассеянии «момента импульса» rvu|m u| с «интенсивностью» 4π√|ф|, где ф = – α/rv , через сферу радиуса rv , а также то, что в наших предположениях
С ≈ rp)/muu2 . (5)
«Рассеяние момента количества движения»: по размерности действие совпадает с моментом импульса. Экстремум действия в лагранжевой формулировке механики дает уравнения движе- ния. Выражение 4πr2m’ тоже размерности действия, но определяет генерацию массы в объеме шара радиуса r и истечение ее в единицу времени. Этот поток массы существует в октетном пространстве и определяется его структурой. Запись уравнений движения и состояний в форме dU/dz = 0 определяет экстремальные условия процесса генерации массы и энергии, потока локальных времен {τ}, пространств Vr и Vp (в общем случае совокупность условий в формуле dU/dz = 0 может включать «горизонтальные» террасы). В этом состоит смысл обобщения принципа наименьшего действия Гамильтона - Остроградского.
Отрицательность инертной массы на границе v (и «чуть далее», вглубь материи) при u > с означает, что явление «инертная масса» обеспечивается тахионами (отрицательным давлением). Но в «релятивистском» определении тахионов «мнимая» единица, возникающая при нормировке на постоянную Лобачевского, такая что ii = -1, отлична от всех единиц алгебры октав. При этом надо иметь в виду поведение радиальной части «классической» волновой функции свободной частицы (или помещенной в центральносимметричное поле, в частности, кулоновского типа) вблизи начала координат: в «центре» частицы ее, частицы, нет. То же относится к ядрам звезд. Существует трехмерный кратер с двумя брустверами: ближний к центру «экранирует» область с mи < 0, а положение второго бруствера определяет динамику отпочкования материи от области ее рождения (решения см. в [5, 10]). В теориях ХХ века эти «внутренности» бесструктурны. Исключение составляет теория элементарных частиц, базирующаяся на опытах по рассеянию частиц друг на друге. Эта «теория внутренностей» в силу своего назначения вынуждена заниматься исследованием областей r ≤10-14 м (для звезд, соответственно, r ≤102 м). Из [2] следует, что типичные размеры неоднородностей в Метагалактике образуют логарифмический ряд. ряд. Внутри «средней» звезды характерные размеры суть 102 ÷103 м (гребень первого бруствера, порядок гравитационного радиуса rg), 106 ÷ 107 м («математическое ожидание» положения гребня второго бруствера, субпланета, «прощупываемая» благодаря тонкой настройке параметров довольно грубых полуклассических систем уравнений (5) и (6) в [3, 5]) и 1010 ÷ 1011 м (оптическая поверхность светила). Для построения более точной картины рождения планет нужно, однако, решать системы полных (аксиально симметричных) уравнений, а тем более – не ограничиваться приближением (*).
Рассеяние материи (массы и энергии вещества и полей с характерными скоростями с < u) порождает гравитацию, а провремя Т = С(x, y, z, px, py, pz) + ςt по отношению к гравитации является первичной сущностью. Вместе с тем геометрически величина m’ связывает физическое пространство-время и энергию-импульс в одно (октетное) пространство, т.е. определяется его структурой.
Если проявленный конденсат материи в макромире при малых скоростях, силах и мощности «управляется» механикой Гамильтона, то негамильтоново рождение материи «из ничего» и уже проявленной материей в локальных областях v C V3 по сценарию h(t) создает экспоненциальный «пузырь» по измерениям x, y, z, px, py, pz (ср. с рядом чисел Фибоначчи, в пределе переходящим в экспоненту). Это выясняется без привлечения механики Гамильтона уже при анализе вклада функции С(x, y, z, px, py, pz), определенной по (5), в системе отсчета наблюдателя (r = 0, p =0):
откуда r´ = r´oe±Ωt, p´ = p´oe ±Ωt, где Ω =m´/ |mи| . Так как скорости галактик растут по закону v ≈Hr, где Н - постоянная Хаббла (А.Сэндидж, 1968 г.: Н ≈ 75.3 ±17 км / (с Мпс)), то m´/ |mи| ≈ 2.43.10-18 /c - это темп приращения массы на единицу проявленной массы в v C V3 (в масштабах Метагалактики). В пределах справедливости равенства kmи = mг , принимая k = 1, получим там в v´ C v, где употребима местная ньютоновская аппроксимация U = - α /r, что m´≈(|mи|/r)3/2 √G , см. выше, и G ≈ 6,....10-11 Н м2/кг2. То есть все ранние выводы о массе и размерах Метагалактики были получены в рамках локальных законов тяготения, приближенно выполняемых в макромире (ОТО также может быть сведена к постньютонову приближению).
Гравитацию бессмысленно рассматривать вне материи, т.е. при тождественно равном нулю втором кватернионе октетного пространства (в ОТО - при «отрыве» псевдотензора плотности энергии-импульса гравитационного поля tik от Rik, т.е. от метрического тензора gik; «устранение» псевдотензорности tik достигается, по существу,за счет его «подавления» тензором Тik в сумме Тik+ tik).
Отрыв фундаментальной структуры октетного пространства от имманентной ей «гравитации» в моменты времени t > 0 означал бы отказ от идеи развития материального мира и возврат к лапласовскому детерминизму - на качественно новом уровне. И в космологии нельзя рассматривать факт расширения пространства вне факта рождения «данной в ощущениях» материи «из ничего», т.е. из других, скрытых ее форм.
То, что ныне принимается за гравитацию, отсутствует «внутри» элементарных частиц и внутри (в керне) звезд, что указывает на внешнее давление тахионной жидкости в пространстве с вихревыми источниками (для двумерного пространства ТФКП исследование проведено в [8]; в случае движения пробных тел вблизи источника массы их траектории огибают центр «тяготения» согласно решениям [3], что указывает на «гравитационные эффекты» в октетном пространстве, структурированном системами уравнений (2), см. с. 88 в [3], и их кольцами, см. с. 49 в [2]).
В общем случае провремя Т должно содержать аксиальные члены (в форме «следов» от них - псевдоскаляров). В области v при t ≈ 0 вторые члены справа системы (3) дают асимметричный вклад в скорости и силы, если C ↔ rot G1 и/или C ↔rotp G2 . Если C ↔rot G1 , то первое уравнение при отражении координат «замедляется», а второе «усиливается» (по-видимому, первопричиной барионной асимметрии Метагалактики является асимметричный механизм генерации материи, а аннигиляция барионов В и антибарионов В*, если она имела или имеет место, и «случайный барионный остаток» dB << B - его следствия).
Если в С - следы аксиальных членов (в октетном пространстве О - вихреисточники, С ↔rot G), то провремя определяет асимметрию левого и правого - в микромире и Метагалактике.
Перспективы экстенсивного развития теории (1), как и подхода в целом: 1) вариация условий (*) и потенциальной функции U; 2) решения на втором и последующих шагах рекуррентных формул; 3) учет члена ĤН/mи2u4 в первом уравнении системы (3) в [3]; 4) численные решения полной системы уравнений расширенным методом Рунге - Кутта; 5) общее решение полной системы уравнений (без специального «квантования»); 6) использование более общих операторных схем; 7) использование моделей арифметики для микромира; 8) расширение метода геометризации с пространств целочисленных измерений на пространства фрактальной размерности.