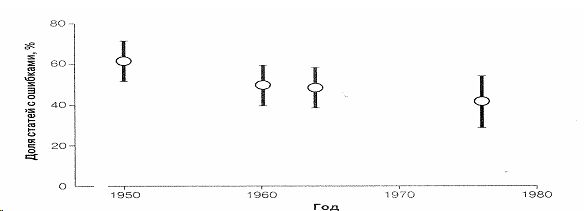
Рис. 1.
Как мы видим, статистические ошибки встречаются примерно в половине статей. Врачам известно множество методов диагностики и лечения, эффективность которых была «доказана» статистическими методами и которые не выдержали проверки практикой. Все это наводит на мысль, что статистические методы слишком трудны для понимания. Между тем даже начального знакомства со статистикой в сочетании со здравым смыслом обычно достаточно, чтобы понять, что предлагает нам автор в качестве «доказательств». Ошибки редко связаны с тонкими статистическими вопросами. Как правило, это простейшие ошибки, такие, как отсутствие контрольной группы, использование неслучайных выборок или пренебрежение статистической проверкой гипотез. Получается, исследователь заявляет о «статистически достоверном» эффекте лечения, редактор помещает статью в журнал, врач, неспособный критически оценить публикацию, применяет сомнительный метод лечения. В конечном итоге больной подвергается ненужному риску и не получает эффективного лечения.
Корни такой математической некомпетентности врача следует искать, в первую очередь, в несовершенстве системы вузовского образования. Каждый вузовский курс призван внести свой вклад в реализацию общих требований высшего образования. При этом в медицинских вузах особая роль принадлежит фундаментальным общетеоретическим курсам, и не в последнюю очередь высшей математике, поскольку математика - универсальный язык для описания процессов и явлений различной природы, без овладения которым сегодня немыслима ни качественная подготовка, ни эффективная деятельность специалиста. Устранение противоречий между тем, что и как студент изучает в медицинском вузе, и тем, что и как ему предстоит делать в своей профессиональной деятельности, определило цель нашего исследования. Для этого необходимо, в первую очередь, выявить оптимальное содержание курса высшей математики, направленного на повышение профессионального мастерства будущих медиков, а также оптимальные условия его проведения.
Одним из этих условий является наличие у студентов внутренней мотивации к изучению данного курса, которую можно обеспечить с помощью примеров, имеющих определенную связь с медицинской практикой. В частности, глядя на график на рис.1, можно подумать, что доля статей с ошибками с годами снижается. Убедиться, что это не так, можно, построив 95% доверительный интервал для последней точки. Последняя точка соответствует периоду с января по март 1976 г. Из оригинальных статей, опубликованных в этот период, авторы рассмотрели 77, статистические ошибки были обнаружены в 32. Выборочная доля составляет p◦ = 32/77 = 0,42, ее стандартная ошибка Sp◦ = √0,42 (1 - 0,42)/ 77 = 0,056.
Тогда доверительный интервал имеет вид: 0,42 - 1,96 ◦ 0,056 < р < 0,42 + 1,96 ◦ 0,056, то есть 0,31< р < 0,53. В этот интервал попадают обе оценки, сделанные в 60-х годах. Это позволяет утверждать, что ситуация не меняется к лучшему.
Примеры подобного типа мы приводим студентам-медикам в курсе математической статистики при изучении темы «Доверительные интервалы», демонстрируя таким образом не только необходимость владения врачами математико-статистическим аппаратом для проведения своих медицинских исследований, но и умение критически оценивать готовые результаты при анализе конкретных профессиональных ситуаций.
Литература:
- Платонов А.Е. Статистический анализ в медицине и биологии: задачи, терминология, логика, компьютерные методы. - М.: Издательство РАМН, 2000. - 52 с.
- С. Гланц. Медико-биологическая статистика. Пер.с англ. - М., Практика, 1998. - 459 с.



