Работа является продолжением исследований по теории устойчивости для уравнений с почти периодическими коэффициентами, выполненные в последнее десятилетие группой математиков г. Омска (см. работу [1] и ссылки в ней).
Рассматривается динамическая система:
![]()
Здесь An , Bn – почти периодические матрицы порядка N , ξn – независимые случайные величины со значениями в C, M [ξn]=0, D [ξn]=1. Почти периодичность по дискретному времени означает выполнение критерия компактности Бохнера [2]. Под решением системы (1) понимается случайная функция со значениями в CN , с вероятностью единица удовлетворяющая (1) на каждом промежутке [0,N] C z.
Будем говорить, что решение xn = 0 экспоненциально устойчиво в среднем квадратическом, если существуют константы α> 0 , β > 0 такие, что для любого решения xn матрица hn = M [xn, xn*] удовлетворяет оценке
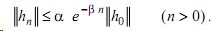
Здесь и далее || · || - эрмитова норма матрицы, * означает транспонирование и комплексное сопряжение. Обозначим Н - конус эрмитово-неотрицательных матриц порядка N .
Т Е О Р Е М А. Пусть существует почти периодическая матрица Гn с отделенным от нуля определителем такая, что при любых n ≥ 0 , h € H имеет место неравенство
![]()
при этом левая часть (2) отлична от тождественного нуля на каждом ненулевом решении h =hn системы h n+1=AnhA*n + BnhB*n со значениями в Н. Тогда решение xn =0 системы (1) экспоненциально устойчиво в среднем квадратическом.
ЛИТЕРАТУРА.
- Романовский Р.К., Троценко Г.А. Метод функционалов Ляпунова для линейных дифференциально-разностных систем нейтрального типа с почти периодическими коэффициентами // Сиб. матем.журн. 2003. Т. 44, №2. С.444-453.
- Левитан Б.М., Жиков В.В. Почти периодические функции и дифференциальные уравнения. М.: Изд-во МГУ, 1978.



