На сегодняшний день, в связи с интенсивным развитием информационных клинических систем появляется возможность решения диагностических задач путем создания качественно новых прикладных систем интеллектуального анализа данных. К классу диагностических задач можно отнести задачу выявления меры влияния синусового узла при мерцательной аритмии для прогнозирования возможности восстановления и сохранения синусового ритма.
Прогноз возможности восстановления и сохранения синусового ритма при мерцательной аритмии важен при выборе стратегии лечения больного. Выявление меры влияния синусового узла при мерцательной аритмии позволяет прогнозировать результаты дефибриляции и трепетания предсердий антиаритмическими препаратами [4]. Решение проблемы полезности восстановления синусового ритма обычно опирается на общеклинические методы исследования, что не всегда позволяет получить правильные результаты. Врачебные алгоритмы оценки и прогнозирования развития мерцательной аритмии и ее исходов относят к эвристическим процедурам. Врачи при принятии той или иной прогностической концепции чаще всего ссылаются на опыт и интуитивную диагностику.
Известен способ корреляционной ритмографии, позволяющий давать прогностические оценки возможности восстановления синусового ритма. На плоскости отмечаются точки (RRi, RR i+1), где i = 1, 2, ..., n - 1, n - количество RR интервалов на электрокардиограмме. Полученная совокупность точек называется авторегрессионным облаком (АРО) [1]. В зарубежной литературе эта же совокупность точек известна также, как скаттерограмма [6]. При наличии правильного ритма сокращения желудочков скопление точек образуется на биссектрисе координатного угла. Умеренная синусовая аритмия приводит к образованию АРО в виде эллипса или круга.
При благоприятном прогнозе на восстановление синусового ритма на АРО точки группируются на сравнительно ограниченной округлой площади, выраженное сгущение точек наблюдается на биссектрисе. Сгущение может быть в центре, в левом нижнем и правом верхнем углу АРО. При сомнительном прогнозе на восстановление синусового ритма на АРО образуется несколько симметрично расположенных относительно биссектрисы совокупностей точек, либо имеет место широкое рассеивание точек на плоскости.
В работе [4] описан геометрический алгоритм распознавания класса АРО, базирующийся на поиске сгущения точек в заданной экспертом зоне. Алгоритмы распознавания АРО используют разделение гиперплоскостью мономодальных и немономодальных классов на основе выделенных информативных признаков оценки микроструктуры и макроструктуры ритма. Апробация указанных алгоритмов распознавания показала, что формализованные алгоритмы принятия решений дают неверные результаты в пограничных случаях, где как раз особенно необходима объективность диагностики.
Высокую производительность интеллектуальных информационных систем решения диагностических задач может обеспечить моделирование искусственных сетей (ИНС). Искусственная нейронная сеть (neural network) представляет собой распределенный параллельный процессор, моделирующий способ обработки мозгом конкретной задачи. Знания о способе решения задачи накапливаются в процессе обучения и хранятся в синаптических весах связей между нейронами [3]. В задачах диагностики в реальном времени необходимо создавать быстрые системы. Искусственные нейронные сети в режиме распознавания работают очень быстро, поэтому они могут служить теоретической и практической основой для разработки таких систем. Использование нейронных сетей обеспечивает такие полезные свойства систем, как нелинейность, адаптивность, отказоустойчивость и помехоустойчивость.
На нейрон поступает набор входных сигналов, представляющий собой выходные сигналы других нейронов. Каждый входной сигнал умножается на соответствующий весовой коэффициент связи. Взвешенные весами связей входные сигналы поступают на блок суммирования. Линейная комбинация взвешенных входных сигналов определяет потенциал активации нейрона. Выходной сигнал нейрона определяется путем преобразования потенциала активации с помощью активационной функции. Наиболее распространенными активационными функциями являются: пороговая, линейная с насыщением, сигмоидальная, логистическая, шаговая, экспоненциальная и гиперболический тангенс.
Конкретный вид выполняемого сетью преобразования данных обусловливается особенностями ее архитектуры, а именно топологией межнейронных связей, способами обучения сети, наличием или отсутствием конкуренции между нейронами, направлением и способами управления и синхронизации передачи информации между нейронами. Можно выделить три основные топологии ИНС - полносвязные, многослойные и слабосвязные. Многослойные нейронные сети делятся на монотонные сети, сети с обратными связями и без них.
Метод поставленной выше задачи диагностики исходов мерцательной аритмии может базироваться на моделировании однослойной сети прямого распространения с пятью нелинейными нейронами. Входной слой является моделью сенсорных клеток, принимающих двоичные сигналы от внешнего мира. На вход нейронной сети поступают бинаризованные прямоугольные изображения АРО. Во входной слой включается m нейронов Sj, где j=1,...,m (m - количество точек на изображении, содержащем АРО). Если на изображении точка черная, то нейрон считается активным. В этом случае значение элемента одномерного массива, реализующего входной слой, равно единице. Если на изображении точка белая, то нейрон неактивен и значение соответствующего элемента массива равно нулю.
Рассмотрим теоретическую архитектуру ИНС для решения задачи диагностики при мерцательной аритмии [5]. Сигналы поступают в слой ассоциативных клеток ai, где i=1,..,n, которые имеют изменяемые веса связей с сенсорными клетками. Число ассоциативных клеток равно количеству классов АРО. Активность i-й ассоциативной клетки определяется формулой: 
, где wij - коэффициент связи между i-й ассоциативной клеткой и j-й сенсорной клеткой.
Информация от ассоциативных клеток подлежит нелинейной обработке, в результате которой формируется реакция ИНС на входной образ. Для вычисления активности нейрона выходного слоя ri, где i=1, ..., n, используется сигмоидальная функция: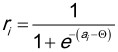 
, где константа Θ выполняет роль порога, влияющего на возбуждение нейрона выходного слоя.
Узнавание класса АРО проводится по самому возбужденному нейрону выходного слоя. Перед использованием нейронной сети в режиме функционирования ее обучают решению конкретной задачи. Парадигмы обучения нейронных сетей разделяют на обучение с учителем и без него. Обучение с учителем предполагает, что для каждого входного вектора из обучающей выборки эксперт определяет целевой выходной вектор. Задача обучения нейронной сети с учителем приводит к общему виду задачи адаптивной фильтрации, постановка которой приведена ниже.
Пусть внешнее поведение некоторой динамической системы описывается множеством данных Т, где
T: {x(i) = [x1(i), x2(i), ... xm(i)]T, d(i);
i = 1, 2, ..., n, ...}
Требуется построить модель выходного сигнала неизвестной динамической системы с некоторыми входами и одним выходом на основе одного нейрона [5].
В контексте рассматриваемой задачи: x(i)- вектор, состоящий из входных сигналов для нейронной сети, d(i) - идеальный отклик выходного нейрона сети. Оптимальные выходные значения для i-го изображения из обучающей выборки все, кроме одного равны нулю. Выход, близкий к единице должен выдавать нейрон, отвечающий за класс, к которому эксперт отнес i-е АРО.
Алгоритм использования сигнала ошибки для коррекции синаптических весов нейрона определяется функцией стоимости, используемой конкретным методом адаптивной фильтрации. Этот вопрос тесно связан с задачей оптимизации, поэтому возможно применение методов оптимизации не только к линейным адаптивным фильтрам, но и к нейронным сетям.
Среди методов безусловной оптимизации можно выделить алгоритмы последовательного спуска, такие как метод наискорейшего спуска, метод Гаусса-Ньютона, метод наименьших квадратов для обучения нейронных сетей, фильтр Винера, алгоритм минимизации среднеквадратической ошибки сети.
ИНС для решения задачи хронопрогнозирования исходов мерцательной аритмии номера может быть обучена по «хеббовскому» правилу - подавление длительной связи [5].
Основной постулат хеббовского обучения звучит так: «Если оба нейрона активны в одно и то же время, то сила связи между ними возрастает. Если из двух нейронов только один активен, то сила связи уменьшается. Если оба нейрона неактивны, то сила связи не изменяется».
В начале процесса обучения ИНС случайным образом заполняется матрица весовых коэффициентов. По выбранному случайным образом элементу обучающей выборки вычисляется активность нейронов входного слоя, ассоциативных клеток и нейронов выходного слоя.
Для i-го нейрона выходного слоя вычисляется вектор ошибки: ei = |ri - di|.
Весовые коэффициенты модифицируются с учетом ошибок по классам следующим образом.
Усиливается связь между черными точками и ассоциативной клеткой, соответствующей номеру правильного класса: если sj = 1 и di = 1, то wij = wij + c · ei, где c - константа, влияющая на скорость и качество обучения.
Ослабляется связь между черными точками и ассоциативными клетками, отвечающими за неправильный класс: если sj = 1 и dk = 0, то wik = wik - c · ek, где k ≠ i.
Ослабляется связь между белыми точками и ассоциативной клеткой, отвечающей за правильный класс: если sj = 0 и di = 1, то wij = wij - c · ei.
Обучающие сеансы повторяют до тех пор, пока суммарная ошибка сети не станет меньше некоторого порогового значения или не закончится обучающая сессия. Лучший результат обучения сохраняется в файл. При загрузке весовых коэффициентов из файла можно использовать сеть в режиме функционирования off-line. При необходимости сеть можно доучить или переучить на новой коллекции тестовых примеров.
Практическая апробация описанных моделей [1, 2, 5] показала, что за 8000 сеансов обучения достигается локальный минимум функции суммарной ошибки. Точка локального минимума не единственна. АРО из обучающей выборки распознаются 100%. Ошибки ИНС допускала при распознавании АРО немономодальных классов из контрольной выборки. Полученные результаты распознавания оказались качественно лучше, чем при использовании формальных алгоритмов классификации АРО на основе выделенных информативных признаков.
Проводимые исследования показывают, что ИНС представляют собой гибкий инструментарий решения диагностических задач, который точно можно настроить под мнение авторитетного эксперта.
Использование многослойных сетей со скрытыми слоями нейронов может позволить решить сложные задачи медицинской диагностики. Распределенная форма нелинейности и высокая связность сети обеспечивают вычислительную мощь многослойных сетей, но, в то же время, усложняют теоретический анализ и визуализацию процесса обучения многослойных сетей. Построение нейронной сети для решения конкретной диагностической задачи можно рассматривать как задачу аппроксимации кривой по точкам (curve-fitting problem) в пространстве высокой размерности. При таком подходе задача обучения сводится к поиску оптимальной поверхности в многомерном пространстве, которая наиболее точно соответствует обучающей выборке. При решении задач многомерной интерполяции используются преобразования, называемые радиальными базисными функциями (radial-basis function). Архитектура нейронной сети на основе радиальных базисных функций строится так, что скрытые нейроны реализуют набор «функций», являющихся произвольным «базисом» для разложения входных образов. [5] Скрытый слой нейронов выполняет нелинейное преобразование входного пространства в скрытое. Размерность скрытого пространства влияет на точность аппроксимации.
Машины опорных векторов (support vector machine), предложенные Вапником, также могут быть использованы для некоторых задач медицинской диагностики. Не обладая априорными знаниями о предметной области, машина опорных векторов может обеспечить хорошее качество решения задачи классификации [3].
В соответствии с принципом «разделяй и властвуй» решение сложной диагностической задачи можно представить в виде объединения иерархии решений более простых задач. Ассоциативные машины статистической структуры позволяют получать усредненное решение на основе мнений нескольких экспертов. В ассоциативных машинах динамической структуры происходит нелинейная обработка выходной информации подблоков сети («экспертов») путем построения нелинейной объединяющей шлюзовой сети, либо иерархии блоков в метаблоки. При таком подходе к решению задач могут быть построены модульные сети, вычисления в которых распределяются по непересекающимся подсистемам, обрабатывающим различные входные сигналы. Модуль интеграции управляет обучением подсистем и принимает общее решение системы по выходным сигналам подсистем.
ИНС позволяют решать не только задачи классификации образов, но и более сложные задачи категоризации. Для выявления сгустков в пространстве входных образов ИНС обучают, используя алгоритмы обучения без учителя (unsupervised learning). При обучении включаются механизмы самоорганизации в физическом пространстве, в фазовом пространстве, в пространстве поведенческих стратегий и решающих правил.
Используя методы синергетики, можно изучать главные компоненты классов, строить «маски» классов, выделять информативные признаки для сетей-классификаторов. Адаптивный анализ главных компонентов может быть проведен с использованием моделирования латерального торможения при организации конкуренции между нейронами выходного слоя или при помощи обобщенного алгоритма Хебба.
В самоорганизующихся сетях под названием карты самоорганизации Кохонена выходные нейроны помещаются в узлах одномерной или двумерной решетки. При обучении нейроны соревнуются за право активации. При этом выходные нейроны настраиваются на представление сгустков в пространстве входных сигналов. По активностям нейронов выходного слоя могут быть построены топографические карты пространства входных образов.
Моделирование ИНС на основе теории информации позволяет решать задачи слепого разделения источников, что является актуальным при выделении важной составляющей зашумленного сигнала при хронодиагностике.
Парадигма диссипативных структур и идеи статистической механики находят свое отражение в проектировании стохастических и детерминированных машин (машина Больцмана, сигмоидальные сети доверия, машина Гельмгольца). Данный комплекс ИНС представляет собой самообучающиеся системы.
В память ИНС могут быть заложены некоторые эталонные образы. Например, визуальные проявления нарушений строения органов. При подаче на вход искаженных изображений (данных, полученных в результате обследования больного) система в результате процессов самоорганизации может «вспомнить» или «восстановить» более подходящий эталонный образец. Задачи такого класса способна решать ИНС с архитектурой Хопфилда.
Парадигма динамического хаоса нашла свое отражение в нейродинамическом программировании. Процессы самоорганизации рассматриваются в фазовом пространстве - в пространстве состояний системы. Перед принятием решения последствия предыдущего решения предсказываются на некоторый интервал будущего. Оптимальное планирование заключается в поиске баланса между текущими и будущими затратами.
Алгоритмы обучения рекуррентных сетей, построенных на нейродинамических моделях, принимают форму нелинейного динамического уравнения, которое управляет расположением аттракторов для закодированной информации или для обучения временных структур [3]. Процессы самоорганизации сопровождаются возникновением самоподобных геометрических структур, повторяющих себя в разных масштабах - фракталов.
Выводы
1. Нейродинамическое программирование может быть использовано при разработке аниматов (искусственных систем, способных приспосабливаться и решать определенные задачи во внешней среде). Адаптивное поведение таких систем могут обеспечить нейросетевые адаптивные критики и организация эволюционных процессов обучения.
2. Модели ИНС, инвариантные к размеру и расположению классифицируемых форм на изображении, могут быть построены на основе ИНС с архитектурой когнитрона и неокогнитрона - многослойных самоорганизующихся нейронных сетей, которые моделирует систему восприятия человека.
3. Применение междисциплинарного подхода, методов кибернетики и синергетики в проектировании искусственных нейронных сетей для решения диагностических задач предоставляет возможность перспективного развития современных интеллектуальных систем хрономедицины.
Список литературы
- Пятакович Ф.А. Алгоритмы классификации степени активности автономной нервной системы на базе нейрокомпьютинга. /Ф.А. Пятакович, Л.В. Хливненко, Т.И. Якунченко // Международный журнал прикладных и фундаментальных исследований. - 2010. - № 5. - С. 115-119.
- Пятакович Ф.А. Способ диагностики успешности и эффективности биоуправляемого игрового тренинга по динамике отношения пульса и дыхания на основе использования обучающихся нейронных сетей / Ф.А. Пятакович, Т.И. Якунченко // International journal on immunorehabilitation. Международный журнал по иммунореабилитации. - 2010. - Т.12. - № 2. - С. 226.
- Хайкин С. Нейронные сети: полный курс // C. Хайкин. - 2-е изд. - М.: Издательский дом «Вильямс», 2006. - 1104 с.
- Хливненко Л.В. Алгоритмы хронопронозирования исходов мерцательной аритмии //Измерительные информационные технологии и приборы в охране здоровья: межд. науч.-практ. конф. Метромед-99, 29.06-1.07, С-Пб ГТУ, С-Пб., 1999. - с. 94-95.
- Хливненко Л.В. Прогнозирование исходов мерцательной аритмии с помощью искусственной нейронной сети // Информатика: проблемы, методология, технологии: материалы 7-ой межд. науч.-метод. конф., 8-9 февр. 2007 г. - Воронеж, 2007. - с. 467-471.
- Poggio T. Networks for approximation and learning / T. Poggio, F. Girosi // Proceedings of the IEEE. - 1990, vol. 78.- p. 1481-1497.
- Stinton P., Tinker I., Vickery I.C., Yahe S.P. The scatterogram. A new method for continuous electrocardiographic monitoring / P. Stinton, I. Tinker, I.C. Vickery, S.P. Yahe // Cardiovasc. - Res.-1972. Vol. 6. - P. 598-604.