Технологическая операция вертикального гидроразрыва пласта (ГРП) часто применяется на газодобывающих промыслах для интенсификации притока флюида к скважине. Широкое практическое применение ГРП стимулирует научные и промысловые исследования по изучению закономерностей фильтрации газа к скважинам с трещинами гидроразрыва [1-4]. В предлагаемой статье выводится новая формула для расчета дебита газодобывающей скважины после ГРП, расчеты по которой осуществляются намного проще, нежели по формулам [2, 3]. В то же время предлагаемая авторами альтернативная формула дает результаты, отклоняющиеся от результатов [2, 3] в пределах не более 3-5%, что позволяет рекомендовать альтернативную формулу к практическому применению.
1. Геометрическая модель призабойной зоны и трещины гидроразрыва
Следуя работе Каневской Р.Д. и Каца Р.М. [3] вертикальную трещину гидроразрыва пласта с конечной толщиной и проводимостью моделируем в виде эллипса с полуосями l и w (рис. 1).
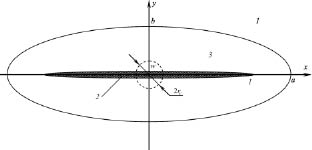
Рис. 1. Схема области фильтрации:
1 - пласт; 2 - трещина; 3 - призабойная зона пласта.
a2 - b2 = l2 - w2 = f2; f - фокусное расстояние конфокальных эллипсов;
rc - радиус скважины. Приток флюида в скважину осуществляется только через трещину
Границу призабойной зоны пласта (ПЗП) моделируем эллипсом, конфокальным к эллиптической трещине. Геометрические размеры и фокусное расстояние f этих двух конфокальных эллипсов будут связаны уравнением
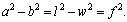
Проницаемости наполнителя трещины 2, призабойной зоны пласта 3 и незагрязненной (удаленной от скважины) части пласта ℓ будем обозначать соответственно как k2, k3 и k1. Установившуюся фильтрацию флюида во всей области фильтрации на рис. 1, как и в [3], считаем подчиняющейся линейному закону Дарси. Вдоль эллиптических границ трещины и ПЗП давление принимается постоянным - названные границы при выводе формулы для дебита скважины принимаются за изобары.
Для вывода формулы дебита скважины с трещиной ГРП предварительно рассчитаем фильтрационные потоки в каждой отдельной части области фильтрации на рис. 1.
2. Расчет притока флюида в скважину через вертикальную трещину гидроразрыва
При расчете притока флюида в скважину из вертикальной эллиптической трещины в [3] в начале координат размещают точечный сток, мощность которого и определяет искомый дебит скважины с ГРП. Однако радиус скважины ≈ 10-15 см, а наибольшая толщина (раскрытие) трещины ≈ 1 см. При таком соотношении размеров радиуса скважины и толщины трещины, моделировать течение к скважине из трещины гидроразрыва при помощи точечного стока в начале координат проблематично, что, по-видимому, и привело авторов [3] к сложному расчетному алгоритму.
Чтобы избежать вычислительных трудностей, связанных с использованием точечного стока, в данной работе на этапе расчета притока флюида в скважину из трещины гидроразрыва последняя моделируется в виде двух одинаковых тонких протяженных прямоугольников с размерами ℓ′ (длина) и 2w′ (ширина). Прямоугольники непосредственно примыкают к скважине по разные стороны от нее и их оси расположены на одной прямой, проходящей через центр скважины. Эллиптическая трещина отождествляется с прямоугольной, если вне кругового контура скважины они обладают равными длинами и площадями поперечных сечений. Исходя из такого определения тождественности двух форм трещин, для геометрических параметров трещин получаем следующие уравнения связи:
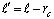
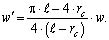(2)
Рассмотрим приток флюида к скважине через трещину гидроразрыва прямоугольной формы. Установившаяся плоскопараллельная фильтрация совершенного газа, как известно, описывается решениями уравнения Лапласа
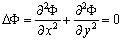(3)
относительно функции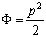 
, где p - давление. Если решение уравнения (3) при соответствующих граничных условиях будет найдено, то поле скоростей найдется из закона Дарси по формуле
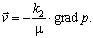(4)
В решаемой задаче расчетная область - прямоугольник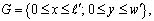 
на сторонах которого задаются следующие граничные условия:
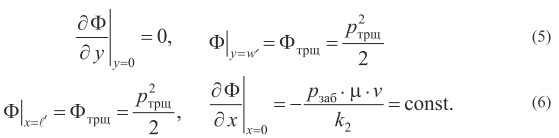
Решение краевой задачи (3)‒(6) строится стандартным методом Фурье и имеет вид
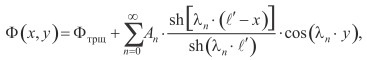(7)
где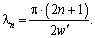 
.
Неопределенные коэффициенты An в формуле (7) находим из последнего граничного условия (6). С помощью известных формул для коэффициентов ряда Фурье, получим, что
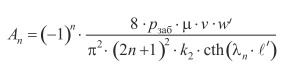(9)
Подстановка коэффициентов An из формул (9) в (7) приводит к следующему выражению для функции :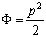
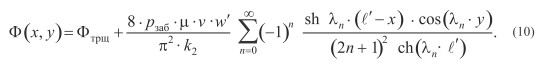
В формуле (10) осталась лишь одна неизвестная величина - скорость фильтрации на границе x = 0 - на входе потока из трещины гидроразрыва в ствол скважины. Для определения неизвестной величины v вычислим среднее значение функции Ф(x, y) на границе x = 0. На основании формулы (10) для среднего значения
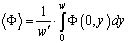(11)
найдем, что
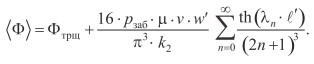(12)
С другой стороны, на границе x = 0 давление должно быть равно забойному давлению и, следовательно, должно выполняться равенство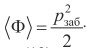 
. С учетом последнего замечания
из (12) для неизвестной величины получим следующее значение:
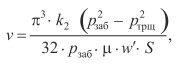(13)
где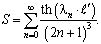 
.
Учитывая, что приток флюида в скважину (подсчитанный для атмосферного давления и пластовой температуры) через трещину гидроразрыва в пласте с толщиной b′ равен величине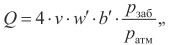 
, для искомой величины дебита Q скважины окончательно получим выражение
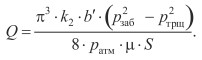(14)
3. Расчет притока флюида к вертикальной эллиптической трещине гидроразрыва от конфокальной границы ПЗП
Рассмотрим теперь фильтрацию в области 3 между трещиной гидроразрыва и эллиптической границей призабойной зоны. На этом этапе исследования форму трещины примем в виде удлиненного эллипса с осями 2l (длина трещины) и 2w (параметр, характеризующий раскрытие трещины). Формула для притока совершенного газа от эллиптической границы ПЗП к эллиптической границе трещины хорошо известна [5] и имеет вид:
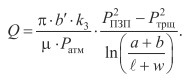(15)
4. Расчет притока флюида к эллиптической границе ПЗП от кругового контура питания
Теперь рассмотрим фильтрацию в 1-й области между эллиптической границей призабойной зоны и круговым контуром питания с радиусом R. Формулу для притока флюида к эллиптической границе ПЗП можно получить методом ЭГДА, исходя из формулы (4)-(25) справочника [6] по расчету электрических емкостей. Формула (4)-(25) в терминах рассматриваемой задачи фильтрации на основании ЭГДА запишется следующим образом:
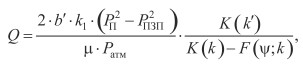(16)
где K(k) и K(k′) = K′(k) - полные эллиптические интегралы 1-го рода с модулями k и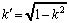 
соответственно, а F(ψ; k) - неполный эллиптический интеграл первого рода. Модуль k и аргумент ψ вычисляются через параметры уравнений границ ПЗП и радиус R кругового контура питания по следующим формулам:
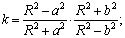
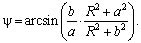(17)
5. Вывод формулы для расчета дебита газодобывающей скважины с вертикальной трещиной гидроразрыва пласта
Формулы (14), (15) и (16) дают систему трех линейных уравнений с тремя неизвестными - дебитом Q и давлениями Pтрщ и PПЗП. Решая методом исключения эту систему уравнений, для расчета дебита скважины с вертикальной трещиной гидроразрыва в ПЗП получим следующую формулу:
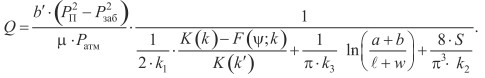(18)
Составляя отношение дебита скважины после ГРП к дебиту этой же скважины без ГРП, для коэффициента эффективности ГРП получаем следующее выражение:
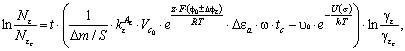(19)
Сопоставительные расчеты дебитов скважин с ГРП по формулам (18) и [2, 3] выявили, что максимальные относительные расхождения не превышают 3-5%. В то же время в вычислительном плане формула (18) для практики предпочтительнее, так как она имеет более простую программную реализацию.
На практике формулы (18) и (19) позволяют рассчитать прогнозный дебит скважины, на которой планируется проведение операции гидроразрыва пласта, и, в конечном итоге, оценить ожидаемую технико-экономическую эффективность от проведения ГРП.
СПИСОК ЛИТЕРАТУРЫ
- Технология проектирования гидроразрыва пласта как элемента системы разработки газоконденсатных месторождений / О.П. Андреев [и др.]. - М.: ООО «Газпром экспо», 2009. -
183 с. - Кадет В.В., Селяков В.И. Фильтрация флюида в среде, содержащей эллиптическую трещину гидроразрыва // Изв. вузов. Нефть и газ. - 1988. - № 5. - С. 54-60.
- Каневская Р.Д., Кац Р.М. Аналитические решения задач о притоке жидкости к скважине с вертикальной трещиной гидроразрыва и их использование в численных моделях фильтрации //
Изв. РАН. МЖГ. - 1996. - № 6. - С. 59-80. - Производительность скважин. Руководство Хеманта Мукерджи. - М.: 2001.
- Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 480 с.
- Иоссель Ю.Я., Кочанов Э.С., Струнский М.Г. Расчет электрической емкости. - Л.: Энергоиздат, 1981. - 288 с.