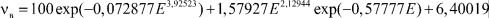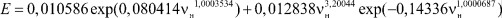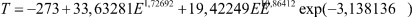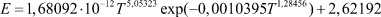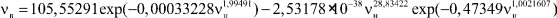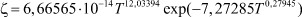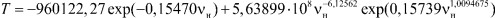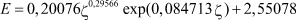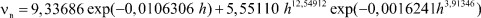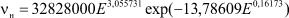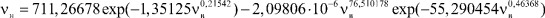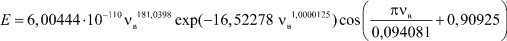Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Поиск новых сорбентов для очистки поверхности водных объектов от нефтяных загрязнений является актуальной задачей. Древесина является дешевым сырьем для получения сорбентов, причем уникальным сорбентом является древесный активированный уголь. В патенте на изобретение [3] приведены данные по экспериментам (табл. 1).

Таблица 1

Экспериментальные данные [3] по сорбции древесных опилок

По данным [3] очистка водной поверхности от нефтяных загрязнений выполняется порошком в виде углистой массы. Она получается при карбонизации измельченных и подсушенных древесных отходов в интервале температур 300-350 oC в инертной среде до степени обугливания 13-16 %.

Цель статьи - факторный анализ выявлением статистических закономерностей процесса сорбции нефтепродуктов углистой массой по данным табл. 1.

В интервале температур 200-300 °C емкость рассматриваемых поглотителей нефти составляет 3,0-3,7 кг/кг (см. табл. 1). Нефтеемкость сорбентов 3,0-4,5 кг/кг можно рассматривать как экономически выгодную. Процесс поглощения нефти с поверхности воды сопровождается и водопоглощением исследуемых сорбентов. При этом степень обводненности нефтешлама с увеличением температуры обжига сорбентов при низкотемпературной карбонизации в сравнении с воздушно-сухим древесным опилом сначала резко снижается (в 1,74 раза при 200 °C) и затем изменяется незначительно [3].

Каждый фактор, приведенный в табл. 1 оценивается относительно самого себя по порядку предпочтения. Процесс установления предпорядка предпочтения среди значений фактора называется ранжированием. В табл. 2 приведено ранговое распределение значений факторов.

Для ранжирования любой из приведенных факторов рассматривается как векторная величина, то есть такая физическая отличительная особенность, которая имеет четкое направление количественного изменения «чем больше, тем лучше».

Таблица 2

Ранговое распределение значений факторов

В табл. 3 приведена корреляционная матрица, полученная после анализа бинарных отношений между всеми принятыми по исходным данным (табл. 1) переменным величинам.

Из общего количества 36 клеток исключили 9 значений, т.к. нет зависимости между толщиной нефтяной пленки и температурой пиролиза древесной фракции, толщиной нефтяной пленки и степенью обугливания, толщиной нефтяной пленки и нефтеемкости сорбента, толщиной нефтяной пленки и содержанием в нефтешламе воды и нефти. Оставшиеся 27 трендовых закономерностей были вычислены в программе CurveExpert-1.3 в виде экспоненциального закона с порогом уровня адекватности выше 0,800.

Таблица 3

Корреляционная матрица факторных связей

Данные (табл. 1) моделировали в программной среде Curve Expert 1.38 [1] (табл. 4).

Модели 2, 3, 5, 6, 8, 9, 10, 12 состоят из двух частей. В модели 2, 3, 6, 8, 10, 12 первая составляющая формулы показывает, что процесс сорбции протекает по закону гибели, а вторая составляющая представляет собой биотехническое возбуждение значений фактора. Эти двухчленные уравнения содержит два устойчивых закона распределения. Первая составляющая является законом гибели, предложенный нами [2], в котором в отличие от закона Лапласа вводится интенсивность гибели (степень объясняющей переменной). Вторая составляющая является биотехническим законом проф. П.М. Мазуркина. Причем первая составляющая является частным.

В модели 5, 9 и 13 первая составляющая является постоянным числом. Модель 1 имеет три составляющие. Причем все они положительно направлены, то есть увеличение нефтеемкости сорбента уменьшает содержание воды в нефтешламе.

Изучив матрицу представленную в табл. 2 и бинарные отношения между факторами, представленными в табл. 3, отбросив все значения с доверием ниже 95 % можно оставить шесть факторных связей 1, 2, 6, 11, 12 и 13 для дальнейшего исследования (табл. 5).

Таблица 4

Бинарные отношения между факторами

Таблица 5

Корреляционная матрица для стратегии исследования

Изучив корреляционную матрицу представленную в табл. 5, у нас получается факторный треугольник, т.е. зависимость нефтеемкости сорбента от содержания в нефтешламе воды и нефти, и наоборот:

Проанализировав представленный граф и данные табл. 3 и 4, и обработав их в программной среде Curve Expert 1.3. нами получены следующие зависимости представленные на рис. 1-6:

Из зависимости представленной на рис. 3, которой соответствует формула модели 1, видно, что первой составляющей можно пренебречь. Вторая составляющая является законом гибели. Третья составляющая является биотехническим законом проф. П.М. Мазуркина.

Из зависимости, представленной на рис. 1, которой соответствует формула модели 13, видно, что изменение нефтеемкости от содержания воды определяется тенденцией (трендом) разностного вида и волновой составляющей.

Из зависимости представленной на рис. 2, которой соответствует формула модели 2, видно, что первой составляющей можно пренебречь. Вторая составляющая является законом гибели.

Из зависимости, представленной на рис. 4, которой соответствует формула модели 6, видно, что первая составляющая является законом гибели. Вторая составляющая является биотехническим законом проф. П.М.  Мазуркина.

Причем первая составляющая является частным случаем биотехнического закона. Поэтому все закономерности получается из одной формулы.

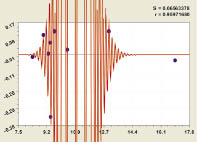
Рис. 1. Нефтеемкость от содержания воды

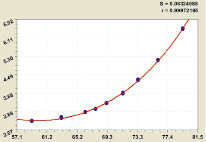
Рис. 2. Нефтеемкость от содержания нефти

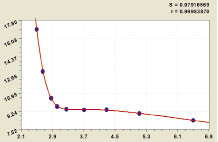
Рис. 3. Содержание воды от нефтеемкости

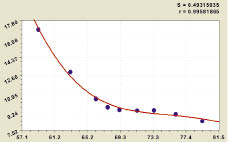
Рис. 4. Содержание воды
от содержания нефти

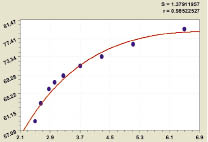
Рис. 5. Содержание нефти от нефтеемкости

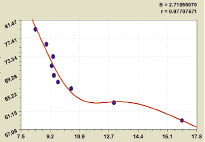
Рис. 6. Содержание нефти от содержания воды в нефтяном шламе

Из зависимости, представленной на рис. 5, которой соответствует формула модели 11, изменение содержание нефти от нефтеемкости происходит по биотехническому закону проф. П.М. Мазуркина.

Из зависимости, представленной на рис. 6, которой соответствует формула модели 12, видно, что первая составляющая является законом гибели (спада). Вторая составляющая является биотехническим законом проф. П.М. Мазуркина.

Высокие коэффициенты корреляции (в правом верхнем углу графиков) уравнений показывают наличие в результатах экспериментов скрытого фактора или даже группы скрытых факторов.

Комплексное изображение нефтеемкости сорбента от содержания воды и нефти в нефтешламе можно представить в трехмерном пространстве (рис. 7), которое показывает взаимосвязь между факторными связями.

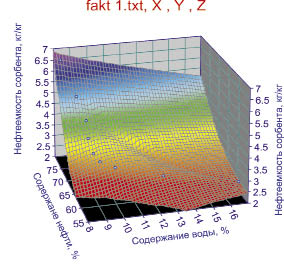
Рис. 7. Зависимость нефтеемкости сорбента от содержания воды и нефти в нефтешламе

Был проведен процесс математического моделирования, т.е. произведена формулировка законов, связывающих основные объекты модели; адекватность модели; анализ математической модели и модернизация этой модели. Анализ математической модели позволяет проникнуть в сущность изучаемых явлений.

По статистическим моделям возможно дополнительное исследование добротности различных сценариев, т.е. детальное изучение зависимостей нефтеемкости сорбента от содержания воды и нефти и наоборот.

Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603 МОН РФ.

Список литературы

1. Мазуркин П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: учеб. пособие для вузов / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МарГТУ, 2006. - 292 с.
2. Мазуркин П.М. Статистическое моделирование. Эвристико-математический подход. - Йошкар-Ола: МарГТУ, 2001. - 100 с.
3. Пат. 2088725 Российская Федерация МПК6 E02B015/04 C09K003/32, Способ очистки водной поверхности от нефтяного загрязнения / Хасанов И.Ю.; Рогозин В.И.; Танатаров М.А.; Хасанов Р.Ю.; заявитель и патентообладатель Хасанов Ильмер Юсупович. - № 95112899/13; заявл. 07.24.95; опубл. 08.27.97.