Бесконечная итерация определенных генераторов G, в том числе и прямоугольных (в частности, видоизмененной кривой Коха K(5/3)), на отрезке конечной длины приводит к формированию бесконечной фрактальной линии. Для моделирования с помощью этого метода вероятных конфигураций межфазных границ на поверхности композиционных покрытий достаточно получить предфрактал на совокупности простых геометрических 2D-фигур, которые можно рассматривать в качестве сечений 3D-многогранников – простейших аппроксимантов формы микрочастиц фаз [1, 2].
Для моделирования могут быть использованы некоторые из сеток Кеплера-Шубникова, которые включают в себя тетрагоны {4} (т.е. квадраты) в виде тел и/или лакун (например, сетки, производные от сеток Кеплера 4444, 488, 46.12) [3]. В этом случае может быть получена информация не только о квазифрактальном характере межфазных границ и их относительной поверхностной концентрации, но и о лакунарных характеристиках поверхности (распределении по поверхности и дискретном лакунарном спектре в виде гистограмм). Для анализа возможных конфигураций использованы результаты модулярного дизайна полигонных и фрактальных структур в 2D-пространстве [4-6] и методика формирования мультифрактальных множеств замкнутых кривых, упорядоченных в 2D-пространстве с использованием 2D-сеток [7, 8].
Прямоугольный генератор К(5/3) может рассматриваться как первый член двух гомологических рядов прямоугольных генераторов К((n + 4)/(n + 2)) и К((4n + 1)/(2n + 1)), где n = 1, 2, 3, …, ∞ (рис. 1).

Рис. 1. Изображения первых четырех членов гомологических рядов прямоугольных генераторов Коха К((n + 4)/(n + 2)) (а) и К((4n + 1)/(2n + 1)) (б)
При многократном действии генератора К(5/3) на периметр ячейки квадратной сетки 44 (где символ означает лакуну) с топологией тетрагонов 4(2) из {4}-тел формируются упорядоченные в 2D-пространстве четырехугольные снежинки с топологией связности вершин 4(3), а {4}-лакуны с вершинной топологией 4(2) превращаются в канторову пыль (с лакунарной топологией 4(2) и 2(2)–2(1) в соотношении 1:4) (рис. 2).
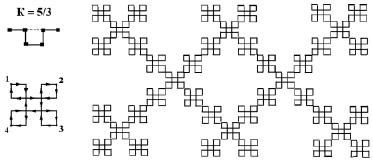
Рис. 2. Изображения прямоугольного генератора К(5/3), схемы его действия внутри 4-лакуны сетки Кеплера-Шубникова 44 и фрагмента лакунарного предфрактала 3-го поколения
При действии прямоугольных генераторов следующих членов гомологического ряда К((n + 4)/(n + 2)) на сетку 44 происходит закономерное затупление вершин снежинок Коха, а в канторовой пыли вторичные лакуны приобретают вершинную топологию 1(2)–3(1) и образуют изолированные пары. При действии прямоугольных генераторов членов гомологического ряда К((4n + 1)/(2n + 1)) на сетку 44 происходит закономерное расщепление вершин снежинок Коха, а в канторовой пыли лакуны также закономерно изменяют вершинную топологию до 1(2) –3(1).
В гомологических рядах генераторов К((n + 4)/(n + 2)) и К((4n + 1)/(2n + 1)) с каждым i–м поколением длина замкнутой фрактальной кривой возрастает по соответствующим законам Li = (n + 4)Li-1/(n + 2) и Li = (4n + 1)Li-1/(2n + 1). Фрактальные размерности кривых D = ln(n + 4)/ln(n + 2) и D = ln(4n + 1)/ln(2n + 1) при n → ∞ закономерно уменьшаются от 1,465 до значения 1,001.
Отметим, что для других сеток Кеплера-Шубникова, содержащих связанные между собой вершинами или изолированные {4}-лакуны, результаты действия генераторов – членов указанных гомологических рядов – аналогично. Отличия состоят лишь в разной конфигурации снежинок из {n}-тел и топологии связанности квадратных лакун в соответствующих предфракталах. Однако именно эти отличия при использовании разных сеток Кеплера-Шубникова для аппроксимации формы микрочастиц поверхностных фаз предопределяют многообразие конфигураций квазифрактальных межфазных границ и разнообразие лакунарных характеристик [7, 8].



