Ранее в работах [1, 2] предложена система информационных кодов для детерминистических фрактальных решеток и множеств мультифрактальных кривых. Методом итерационного модулярного дизайна получены серии детерминистических фрактальных решеток с генераторами в виде фрагментов 2D структур и серии мультифрактальных кривых (на основе некоторых сеток Кеплера-Шубникова), обладающих свойствами канторова множества [2]. Определены и проанализированы основные характеристики фрактальных структур и их лакунарные спектры. Установлено, что полученные в [1–4] теоретические данные о 2D-структурах и фрактальных структурах, упорядоченных на 2D-сетках (сетках Кеплера и некоторых сетках Кеплера-Шубникова), могут быть использованы при оценке вклада геометрической конфигурации межфазных границ в эффект синергизма антифрикционных свойств компонентов композиционных покрытий при трении [5–7].
Для получения итерационным методом квазифрактальной конфигурации межфазных границ на поверхности композиционных покрытий в [5, 6] использовали меандроподобный треугольный генератор К(4/3), а в качестве аппроксимантов конфигураций – сетки Кеплера. Отметим, что данный генератор является первым членом как минимум двух гомологических рядов меандроподобных генераторов, которые применяются при подгонке удельных характеристик межфазных границ при сохранении относительных поверхностей микрочастиц фаз.
В данном случае будем использовать треугольные генераторы Коха гомологических рядов К(2(n + 1)/(n + 2)) (а) и К(2(3n – 1)/3n) (рис. 1). В результате итерации данных генераторов на периметрах {n}-тел сеток Кеплера-Шубникова образуется множество неизолированных фракталов – разнообразных снежинок Коха, упорядоченных в 2D-пространстве.

Рис. 1. Изображения первых четырех членов гомологических рядов треугольных генераторов Коха К(2(n + 1)/(n + 2)) (а) и К(2(3n – 1)/3n) (б)
В треугольных лакунах сеток Кеплера-Шубникова (тригонной {3}, дитригонной 2{3} или тетратригонной 4{3}) формируются определенные мультифрактальные множества кривых, представляющие собой лакунарные мультифракталы с мощностью канторова множества и характерным для них лакунарным спектром (см., например, рис. 2, а).
а)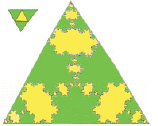 б)
б)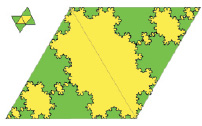
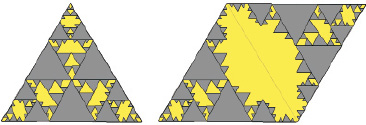
Рис. 2. Лакунарные мультифракталы 5-го поколения при действии генератора Коха вида К(4/3) (вверху) и 3-го поколения при действии генератора вида К(22/12) – 4-го члена ряда К(2(3n-1)/3n) (внизу) на тригонную (а) и дитригонную (б) лакуны сеток Кеплера-Шубникова с вершинными топологиями 333 и (33 + 3333)-(1:1), соответственно
По мере увеличения порядкового номера генератора в каждом гомологическом ряду при итерации наблюдается закономерное увеличение длины квазифрактальной кривой и изменение ее хаусдорфовой размерности в интервале 1 < D < 2 в соответствии с зависимостями
D = ln2(n + 1)/ln(n + 2)
и
D = ln2(3n – 1)/ln3n.
Происходит также все более ярко выраженное расщепление вершин снежинок Коха. Для лакунарных мультифракталов наряду с нарастающим расщеплением выступов-вершин каждого фрактала в отдельности наблюдается либо сохранение качественных характеристик лакунарного спектра (для членов ряда К(2(n + 1)/(n + 2))), либо закономерное качественное и количественное изменение спектра в сторону увеличения числа гармоник основных линий (для членов ряда К(2(3n – 1)/3n)) (рис. 2, сравни для а и б верхние и нижние мультифракталы).
Таким образом, методом итерации треугольных генераторов на периметрах определенных сеток Кеплера-Шубникова может быть получено множество вариантов конфигураций фрактальных кривых. Наборы этих кривых позволяют аппроксимировать конфигурации вероятные межфазных границ и получить соответствующие удельные характеристики – поверхностные доли этих границ и качественный вид спектра лакун, в которых могут находиться ультрадисперсные примесные фазы или фазы смазочной компоненты композиционного покрытия. Полученные теоретические данные могут быть использованы при регулировании полуэмпирических параметров синергической модели «концентрационной волны», используемой при априорном расчете трибологических характеристик – коэффициента трения и скорости линейного износа – для композиционных покрытий [5–7].



