Известно, что основным технологическим показателем работы электропечных агрегатов (дуговая сталеплавильная печь (ДСП), агрегат «печь-ковш» (АПК)) является скорость нагрева металла. На каждой ступени трансформации электрический режим работы агрегата должен быть организован таким образом, чтобы эта величина достигала максимального значения. Скорость нагрева металла зависит от ряда электрических и технологических показателей плавки: тока электрода IЭ, напряжения дуги UД, степени заглубления дуги в металл, наличия и толщины слоя шлака hШ в плавильном пространстве.
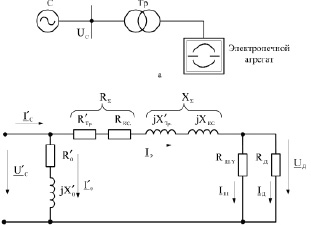
Установлено, что имеется примерно пропорциональная зависимость между т.н. коэффициентом интенсивности нагрева kИ.Н, равным произведению тока дуги на ее мощность, и скоростью нагрева металла vН [1]. Характер зависимости kИ.Н от тока электрода носит экстремальный характер, поэтому легко определить такую величину IЭ, при которой kИ.Н примет максимальное значение. Для определения kИ.Н необходимо составить схему замещения электрической части электропечного агрегата. Поскольку применение kИ.Н оправдано только тогда, когда дуги, экранированные или неэкранированные шлаком, горят над жидким металлом (стадии окисления и рафинировки), схема замещения может быть принята линейной и однофазной, т.к. в этом случае несимметрия и несинусоидальность токов и напряжений в питающей сети выражены настолько, что возможно пренебречь данными явлениями. На рис. 1,б) представлена данная схема замещения, в ней сопротивление RШ.Y, моделирующее ответвление части тока электрода в шлак, учитывается при коэффициенте экранирования дуги kЭ.Д > 1, т.е. в случае, когда дуга экранирована шлаком по всей длине и имеется непосредственный контакт между шлаком и электродом. Для неэкранированных дуг обозначим коэффициент интенсивности нагрева металла как kИ.Н.Н и определим согласно (1):
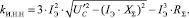(1)
Для дуг, экранированных шлаком, с учетом того, что при значительных величинах hШ часть тока электрода ответвляется в шлак, обозначим рассматриваемую величину как kИ.Н.Э и определим согласно 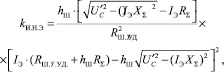(2):
(2)
где RШ.УД.Y – удельное сопротивление слоя шлака единичной толщины (например 1, см).
Если воспринимать зависимость vН = f(kИ.Н) так, как она описана в [1], то получится, что большему значению kИ.Н соответствует большая скорость нагрева металла. Однако более подробные исследования этой зависимости, результаты которых представлены в [2], и наблюдения за работой 330 т. агрегатов «печь-ковш», установленных в Конверторном цехе № 2 ОАО «НЛМК», показали, что при наличии шлака в ковше меньшим значениям kи.н могут соответствовать большие скорости нагрева. Для подтверждения правомерности рекомендаций о поддержании максимума kИ.Н для достижения максимальной скорости нагрева металла согласно (2) был произведен расчет KИ.Н.Э для различных значений тока электрода, а скорость нагрева металла – из решения системы дифференциальных уравнений, описывающих тепловой режим АПК, где первое уравнение будет описывать тепловое состояние металла, а второе – шлака:
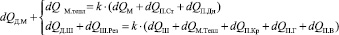(3)
где dQД.М – дифференциал количества теплоты, выделяемого дугой в пределах металла; dQМ.тепл – дифференциал количества теплоты, предаваемого металлу шлаком; k – коэффициент, определяющий долю теплоты, обусловленной электрическим нагревом, в общем количестве теплоты, получаемом металлом и шлаком (согласно [1] при рафинировке на электрический нагрев приходится около 50 % приходной части теплового баланса (остальное обусловлено химическими реакциями и теплотой, вносимой предварительно подогретыми шлакообразующими и присадками)); dQМ – дифференциал теплосодержания металла; dQД.Ш – дифференциал количества теплоты, выделяемого дугой в пределах шлака; dQШ.Рез – дифференциал количества теплоты, выделяемого в шлаке за счет резистивного нагрева; dQШ – дифференциал теплосодержания шлака; dQП.Дн, dQП.Ст, dQП.Кр – дифференциалы потерь тепла конвекцией и излучением через днище, стенки, крышку ковша соответствунно; dQП.Г, dQП.В – дифференциалы потерь тепла с отходящими газами и охлаждающей водой [1, 3].
б
Рис. 1. Схемы замещения электрической части электропечного агрегата: а – поясняющая схема электроснабжения; б – схема замещения для определения kИ.Н: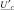
, 
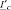– линейный ток и фазное напряжение, потребляемые печным трансформатором из сети; 
, 
, 
, 
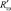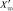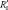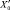– сопротивления короткого замыкания и холостого хода печного трансформатора соответственно; RКС, XКС – сопротивления короткой сети; RШ.Y – сопротивление слоя шлака, приведенное к напряжению дуги; RД – сопротивление дуги. 
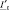– ток холостого хода печного трансформатора; 
, 
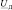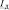– ток и напряжение дуги; 
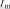– ток, протекающий через слой шлака. Все токи, напряжения и сопротивления приведены к вторичному напряжению печного трансформатора
Расчет осуществлялся для первых трех ступеней трансформации потому, что максимуму kИ.Н.Э на них соответствуют токи, не превышающие допустимых для печного трансформатора значений. Результаты этих расчетов представлены на рис. 2. Сопоставление kИ.Н.Э и скорости нагрева металла показало, что на одной ступени трансформации при постоянной толщине шлака большим значениям kИ.Н соответствуют большие значения vН.
а)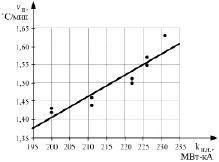
б)
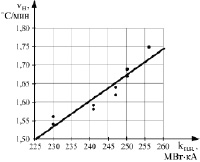в)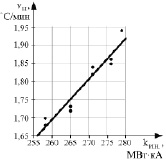
Рис. 2. Зависимости скорости нагрева vН металла от коэффициента интенсивности нагрева металла kИ.Н.Н для дуг, экранированных шлаком:а – для первой ступени трансформации; б – для второй ступени трансформации; в – для третьей ступени трансформации.
Необходимо также рассмотреть данную зависимость для случаев, когда дуга горит без экранирования. Исследуемые агрегаты из-за опасности повреждения крышки в таком режиме не работают, поэтому скорость нагрева металла была определена расчетным путем, исходя из того, что металл поглощает 100 % мощности, выделяемой участком дуги, погруженном в него, и 25 % мощности открытого участка дуги за счет отражения на него лучистых потоков от футеровки [1]. Остальные 75 % энергии открытого участка дуги теряются через крышку, с охлаждающей водой и отходящими газами. Исходя из этого, было составлено уравнение теплового баланса:
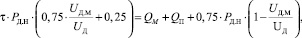(4)
где UД.М – падение напряжения на участке дуги в пределах металла, определяемое с учетом того, что градиент напряжения столба неэкранированной дуги равен 1,0 [1]; QМ – теплосодержание металла; QП – тепловые потери конвекцией и излучением через стены и днище ковша; PД.Н – мощность неэкранированной дуги.
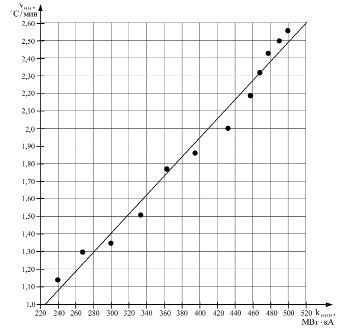
Рис. 3. Зависимость скорости нагрева vН.Н металла от коэффициента интенсивности нагрева металла kИ.Н.Н для неэкранированных дуг
Расчет скорости нагрева металла, не экранированного шлаком, осуществлялся для каждой ступени трансформации, ток электрода принимался равным соответствующим эксплуатационным значениям. Результаты расчетов скорости нагрева и kИ.Н.Н представлены на рис. 3. Из их анализа можно заключить, что при горении неэкранированных дуг на жидкий металл скорость его нагрева имеет один и тот же характер зависимости от kИ.Н.Н для всех ступеней трансформации.
Можно сделать вывод, что при определении параметров оптимального электрического режима достижением максимума kИ.Н для экранированных дуг следует анализировать работу агрегата на определенной ступени трансформации при определенной толщине шлака, а для неэкранированных дуг зависимость vН = f(kИ.Н) можно использовать для всех ступеней трансформации.