Для изучения этого вопроса была рассмотрена схема рабочего процесса перемещения жидких фракций по горизонтальному желобу трапецеидальной формы поперечного сечения с наклоном стенок в 45°. Жидкие фракции плотностью ρ самотеком поступают в желоб глубиной h и перемещаются под действием вращающегося в желобе спирального винта с шагом s, примерно, равным диаметру спирали d.
При перемещении материала винтовой поверхностью, спираль укорачивается, поэтому на противоположном от привода конце спирали устанавливается упорное подшипниковое устройство.
В случае движения жидкости и проволочного винта в канале скорость перемещения жидкости относительно пружины u0 = u – v где u – линейная осевая скорость движения проволочного винта, а v – осевая скорость жидкости относительно канала.
Получено уравнение для определения осевой скорости жидкости:
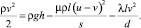
Приведя его к виду, удобному для решения, получим квадратное уравнение относительно v:
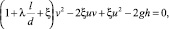
где ξ = μl/s; μ – динамическая вязкость; l – длина канала.
Величина дискриминанта этого уравнения должна быть положительна, а линейная скорость движения удовлетворять неравенству:
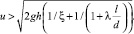
Решая квадратное уравнение, получаем значение скорости движения жидких фракций по желобу:
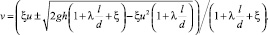
Совпадение результатов эксперимента с теоретической зависимостью подтверждает механизм движения жидкости в условиях вращения спирального винта в желобе.



