В лабораторной практике при решении задач газового анализа широкое распространение получили масс-спектрометрические и газохроматографические средства измерений парциальных давлений составляющих смеси газов, обладающие высокой чувствительностью, точностью и разрешающей способностью [1, 2].
Однако, развитие современной технологии металлургических предприятий, а также возрастающие потребности в чистых газах других отраслей – приборостроение, светотехническая, химическая и ряд других отраслей промышленности, требуют создания новых типов универсальных и специальных анализаторов для оперативного контроля микропримесей в чистых газах. При этом на первый план выдвигаются проблемы выбора материалов для газовых сенсоров [3, 4].
Среди всего разнообразия газовых сенсоров мы рассмотрим люминесцентные газоанализаторы, представляющие собой некоторую пористую структуру с внедренными в нее молекулами люминофора. Рассмотрение будем проводить на основе термодинамического подхода, подробно изложенного в работе [5].
Термодинамическая модель
Молекулы красителя (например, эозина), адсорбированные на поверхности пористого вещества (например, силикагеля) будем рассматривать как систему невзаимодействующих частиц, погруженную в термостат. Квантовые переходы, обусловленные взаимодействием молекул красителя с термостатом, будут диссипативными (с вероятностью Р) в отличие от взаимодействия с внешним полем (с вероятностью F).
Поскольку подсистема молекул обменивается с термостатом только энергией, то соответствующий им ансамбль частиц будет каноническим. В этом случае выражение для вероятности диссипативных процессов имеет вид [5]:
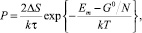(1)
где ΔS – изменение энтропии в диссипативном процессе; Em – среднее значение энергии основного состояния молекул красителя; τ – время релаксации; G0 – энергия Гиббса термостата; N – концентрация молекул красителя; k – постоянная Больцмана; Т – температура термостата
Для функции отклика Ф системы на внешнее поле имеем:
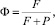(2)
где Р – вероятность диссипативного процесса и определяется (1); F определяет вероятность перехода в возбужденное состояние за счет внешнего поля, причем F = 1/τр, где τр – время жизни возбужденного состояния.
С учетом (1) выражение (2) примет вид:
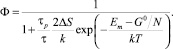(3)
Обозначая предэкспоненциальный множитель в (3) через С, получим
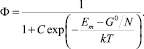(4)
Уравнение (4) можно линеаризовать, в результате чего для относительной интенсивности люминесценции молекул красителя Ф = I/I0 получаем:
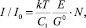(5)
где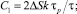 
, E = mhν – плотность энергии внешнего электромагнитного поля; m – число фотонов.
Хотя формула (5) носит приближенный характер, но она полезна для качественного анализа влияния среды (через G0) и условий облучения (через Е) на люминесцентные свойства молекул красителя. В частности, для наблюдения максимальной интенсивности люминесценции нужно подбирать растворитель или твердую основу с минимальной энергией Гиббса. В случае адсорбции молекул на поверхности, необходимо подбирать основу с минимальным поверхностным натяжением, поскольку в этом случае G0 = σS (σ – поверхностное натяжение, S – площадь образца).
Из формулы (5) вытекают и известные факты: линейная зависимость интенсивности люминесценции от концентрации центров свечения N (при не слишком больших значениях N); линейная зависимость интенсивности люминесценции от плотности возбуждения Е (при не слишком больших значениях Е) [6].
Температурная зависимость интенсивности люминесценции определяется в (5), в основном, температурной зависимостью G0 ~ T2, так что I ~ 1/T.
Анализатор кислорода
В большинстве случаев люминесцентный анализатор кислорода представляет собой полимерную пленку с внедренными в нее молекулами органических красителей. Анализ кислорода основан на его способности к динамическому тушению фосфоресценции органических молекул. Активное взаимодействие молекулярного кислорода с триплетными возбужденными состояниями органических молекул обуславливает резкую зависимость кинетики люминесценции последних от количества в системе.
В простейшем случае, имеет место следующее соотношение [7]:
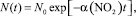(6)
где α–1 – эффективное время жизни Т-центра, зависящее от концентрации О2: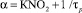 
; K – константа скорости тушения; τp – время жизни возбужденного состояния красителя; N0 – начальная концентрация Т-центров, образованных в результате δ импульсного возбуждения.
С учетом (6) уравнение (5) примет вид:
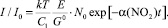(7)
Из графика ln(I/I0) ~ t определяется α–1 и, тем самым, концентрация кислорода.
На практике, однако, указанная процедура извлечения информации о величине NO2 не является корректной и приводит к значительным ошибкам. Это связано с тем, что генерация Т-состояний происходит не мгновенно (в шкале времен α–1), а в период действия источника возбуждения. В этом случае соотношение (6) нарушается и необходимо учитывать деформацию кинетики. Следующим обстоятельством нарушения соотношения (6) является наличие нескольких каналов тушения замедленной флуоресценции красителей. В настоящее время все эти эффекты учитываются в процессе измерений при использовании соответствующих программных средств.
Термодинамические ограничения точности люминесцентного газового анализа
Современный анализатор газа представляет собой информационно-измерительную систему (ИИС). Основной характеристикой ИИС является точность. Точность работы ИИС определяется динамическими характеристиками: быстродействием, помехоустойчивостью, разрешающей способностью. Она определяется как внутренними факторами (структура системы, алгоритм функционирования и обработки сигналов и т.п.), так и внешними условиями (условия измерений, наличие естественных помех и т.п.).
Техническую эффективность ИИС по показателю точности количественно оценивают ошибкой 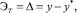[8]:
(8)
где y – вектор фактической реакции системы; y* – вектор желаемой реакции системы.
На каждом этапе элементарного информационного взаимодействия рост энтропии термостата ΔS лежит в пределах 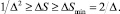[9]:
(9)
Левая граница соответствует предельно необратимой реализации переходного процесса, а правая – оптимальному замедлению его.
С другой стороны, негэнтропийный эффект (эффект упорядочивания в системе, ΔK = –ΔS), согласно [10, 11]:
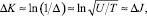(10)
где ΔJ – полученное в процессе измерения количество информации (в нашем случае ΔJ ≈ I/I0 В этом случае энтропийная эффективность ηη информационно-измерительного процесса:
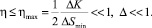(11)
Минимальное значение энтропии реализуется при условии максимума количества информации и с учетом (5) имеем:
ΔJ → max; EN/G0 → max;
G0 → min; σ → min. (12)
Поверхностное натяжение полимерных пленок
Поверхностное натяжение – основная термодинамическая характеристика процессов, связанных с участием поверхностей или границ раздела фаз. Поверхностное натяжение определяет свободную энергию (работу), которую необходимо затратить, чтобы образовать единицу площади поверхности или раздела фаз.
Экспериментальное определение поверхностного натяжения твердых тел (включая полимеры) затруднено тем, что их молекулы (атомы) лишены возможности свободно перемещаться. Исключение составляет пластическое течение металлов при температурах, близких к точке плавления [12]. В связи с этим развито большое количество косвенных методов [13], точность которых оценить довольно проблематично. Для полимеров способы определения поверхностного натяжения обсуждались в работах [14, 15].
В работах [16, 17] нами предложены новые методы определения поверхностного натяжения диэлектриков, включая люминофоры. Методы основаны на размерной зависимости некоторого физического свойства исследуемого материала. Для люминофоров, в частности, – это размерная зависимость квантового выхода люминесценции. В рассматриваемом нами случае кислородного датчика – это зависимость относительной интенсивности флюоресценции молекул красителя от толщины полимерной пленки:
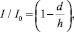(13)
где h – толщина пленки; d – размерный параметр, который связан с поверхностным натяжением полимерной пленки σ соотношением:
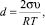(14)
где u – молярный объем; R – газовая постоянная; Т – температура. В координатах I/I0 ~ 1/h получается прямая, тангенс угла которой определяет σ.
В рассмотренном случае молекулы красителя служат своего рода индикаторами поверхностных свойств полимерной пленки. В методе [16] используется размерная зависимость диэлектрической проницаемости диэлектрика. Видимо, этот метод более удобен для определения поверхностного натяжения полимерной пленки, поскольку диэлектрические потери лежат в основе многих методов определения толщины самой полимерной пленки [18].
Поскольку и само поверхностное натяжение пленки становится размерно-зависимой, начиная с некоторого критического значения ее толщины, и также определяется соотношением (13), то ясно, что для люминесцентных газоанализаторов необходимы полимерные пленки как можно меньшей толщины.
Заключение
Основной вывод, который следует из термодинамического подхода к люминесцентному газовому анализу, сводится к возможности синтеза полимерной основы газоанализатора с заданными свойствами путем изменения ее поверхностного натяжения (поверхностной энергии).
Работа выполнена по программе МОН РК 055 «Научная и/или научно-техническая деятельность», подпрограмма 101 «Грантовое финансирование научных исследований». Контракт № 1932.