Фуллерен состава С30 является третьим членом гомологического ряда C6(n + 2) фуллеренов (где n = 1, 3, 4…), формы которых являются производными от полиэдров {(n + 2)44} призматического типа и обладают симметрией соответствующих точечных групп D(n + 2)h. Для фуллерена С30 с симметрией некристаллографической точечной группы D5h (`10m2) существуют две топологически различимые разновидности семнадцатигранников. Один из этих многогранников содержит 3 типа граней (10 треугольных, 2 декагональных и 5 октагональных) и 2 топологически неэквивалентных типа вершин (20 с топологией {38.10} и 10 с топологией {388}) и реализуется в форме усеченной пентагональной призмы. Второй многогранник тоже содержит 3 типа граней (2 пентагональных, 10 гексагональных и 5 тетрагональных) и 2 топологически неэквивалентных типа вершин (20 с топологией {466} и 10 с топологией {566}) и реализуется в форме усеченной пентагональной бипирамиды. Обе изосимметрийные модификации могут быть получены в результате определенных топологических преобразований пентагональной призмы с симметрией D5h.
Для представления полиэдров используем следующие символьные обозначения: Ph – <nv, nr, nh>, где Ph – имя полиэдра, nv, nr и nh – количество вершин, ребер и граней, соответственно. Тогда в результате сплиттинг-преобразования вершин пентагональной призмы и стелейшн-дизайна определенных граней тригональнопризматической бипирамиды можно получить следующую цепочку изосимметричных конфигураций (рис. 1):
пентагональная призма Рp – <10, 15, 7> →
усеченная пентагонпризма tРp – <30, 45, 17> →
пентагональнопризматическая бипирамида РpbiPyr – <15, 30, 17> →
усеченная пентагонбипирамида tРbiPyr – <30, 45, 17> →
пентагонбипирамида РbiPyr – <7, 15, 10> .
Методом анализа фундаментальной области точечной группы симметрии можно перечислить группы симметрии всех возможных симметрийно неэквивалентных разновидностей молекул фуллерена, которые могут возникнуть в результате ее непрерывных деформаций [1]. Для этого необходимо выделить все структурные элементы области с разной размерностью и локальной симметрией. Соотношения таких структурных элементов группы D5h в фундаментальной области для двух форм молекул фуллерена С30 представлены на рис. 2.

а б в г д
Рис. 1. Проекции Шлегеля для изосимметричных (D3h) полиэдров: Рp (а), tРp (б), РpbiPyr (в), tРbiPyr (г) и РbiPyr (д)
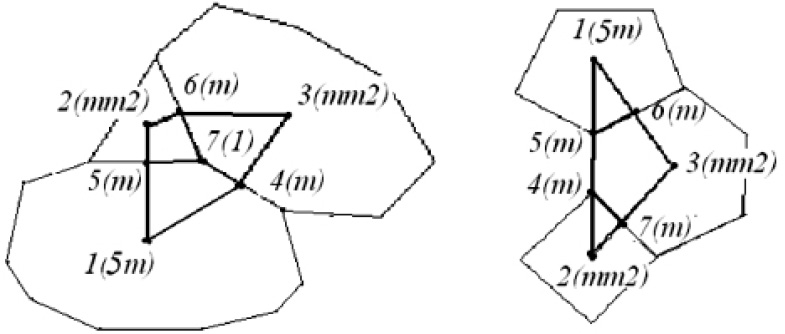
а б
Рис. 2. Соотношения структурных элементов деформационных модификаций фуллеренов С30, полученных в фундаментальной области точечной группы D5h для tРp (а) и для tРbiPyr (б)
Вероятные структурные состояния молекулы фуллерена С30
|
Структурный элемент * |
Размерность |
Симметрия орбиты |
Собственная симметрия |
|
Фуллерен в форме усеченной пентагональной призмы |
|||
|
1 |
1 |
|
5m |
|
2, 3 |
mm2 |
||
|
4, 5, 6 |
m |
||
|
7 |
1 |
||
|
1–5, 2–5, 2–6, 3–6, 3–4, 1–4 |
2 |
|
m |
|
4–7, 5–7, 6–7 |
1 |
||
|
2–6–7–5, 3–6–7–4, 1–5–7–4 |
3 |
|
1 |
|
Фуллерен в форме усеченной пентагональной бипирамиды |
|||
|
1 |
1 |
|
5m |
|
2, 3 |
mm2 |
||
|
4, 5, 6, 7 |
m |
||
|
1–6, 2–6, 2–7, 3–7, 3–4, 1–5 |
2 |
|
m |
|
5–6, 4–7 |
1 |
||
|
1–5–6, 3–4–7, 4–5–6–2–7 |
3 |
|
1 |
Результаты анализа вероятных структурных состояний двух изосимметрийных молекул приведены в таблице. Используемые обозначения структурных элементов фундаментальной области точечной группы D5h для фуллеренов состава С30 указаны на рис. 2, а и 2, б, соответственно.
Можно предположить, что при модифицировании композиционных покрытий наноалмазным порошком фазовая и структурная разупорядоченность углеродсодержащих наночастиц на их поверхности после трибовоздействия может быть обусловлена, в частности, наличием подобных фуллереноподобных наночастиц с симметрией группы D5h или ее вероятных деформационных модификаций. Все эти наночастицы могут рассматриваться как компоненты покрытия, проявляющие свойства твердосмазочных материалов и, следовательно, эффективно влияющие на трибологические свойства поверхности при трении [2–8]. Возможные непрерывные и обратимые структурные фазовые превращения фаз компонентов покрытий, в частности и фуллереноподобных наночастиц, могут быть идентифицированы в соответствии с методиками, представленными в работах [8–14].
Данное предположение об эффективности модифицирования косвенно подтверждается, в частности, результатами трибологических испытаний соответствующих твердосмазочных антифрикционных покрытий, полученных с использованием наночастиц алмаза [15].
Работа выполнена при частичной финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.



