По окончанию высшего учебного заведения, молодой специалист должен обладать, наряду с профессиональными знаниями и умениями, способностью к самообразованию, что и является одной из главных задач образовательного процесса. Основным препятствием в становлении специалиста является формализм знаний студентов. В работе [2] рассмотрены основные причины появления формализма в знаниях студентов, среди которых выделим отсутствие навыков самостоятельной работы. Задача преподавателя – максимально использовать и стимулировать индивидуальную творческую деятельность студента.
Опираясь на исследования Г.Ф. Бушона [1], мы выделяем основные компоненты организации самостоятельной работы студентов в техническом вузе с целью преодоления формализма в знаниях студентов: создание необходимой психологической настроенности студентов на решение задач; прививать умение самостоятельно решать типовые, экспериментальные и творческие задачи, прививать умения самостоятельно проводить научные исследования в частных прикладных задач.
В работе [3] авторы для решения проблемы формализма знаний указывают на то, что необходимо правильно выбрать эффективные способы подачи материала и своевременно выявить усвоенные студентами знания. Преподаватель, организуя самостоятельную деятельность студентов должен подбирать содержательные задачи, разрабатывать систему вопросов для всестороннего анализа задачи, привлекать к ее решению всех студентов.
На примере решения задачи, покажем примерную схему организации самостоятельной работы студентов с целью преодоления формализмов существующих знаний.
Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона плоскости к горизонту 45°. Зависимость пройденного телом расстояния от времени даётся уравнением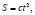 
где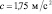 
. Найти коэффициент трения тела о плоскость.
При анализе решения задачи, студенты выполняют следующие задания: расставить все силы, действующие на каждое тело; выбрать соответствующую систему отсчета; написать второй закон Ньютона, в форме векторной и скалярной. Как правило, большинство студентов справляются с таким заданием, поскольку задача типовая. К активному участию в решении задачи привлекаются все студенты: каждый из них готов дать устный ответ на вопрос или продолжить ее решение на доске. В тетради у большинства студентов появляется примерное решение. В случае необходимости решение дублируется на доске. Согласно второму закону Ньютона: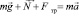 
. В проекциях на выбранные оси второй закон Ньютона:
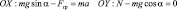
По закону Амонтона: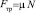 
. Учитывая, 
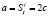получим искомую величину 
.
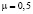Далее преподаватель, активизирует познавательную деятельность студентов, путем методически проработанных вопросов предлагает им переформулировать условие, дополнив и усложнив ее. В ходе обсуждений возможны такие варианты задачи: а) Если клин движется с ускорением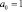 
м/c2. Определить коэффициент трения между телом и клином. Коэффициент трения между столом и клином: 1) отсутствует; 2) 0,1. б) Если клин неподвижен, а система находится в вагоне, который движется с ускорением а0=1 м/c2: 1) вправо 2) влево. Определить коэффициент трения между телом и клином. Коэффициент трения между столом и клином: 1) отсутствует; 2) 0,1.в) Если клин неподвижен, а система находится в лифте, который движется с ускорением а0=1 м/c2: 1) вверх 2) вниз. Определить коэффициент трения между телом и клином. Коэффициент трения между столом и клином: 1) отсутствует; 2) 0,1. После обсуждений по решению усложненной задачи учебную группу делим на подгруппы. Каждая подгруппа решают по выбору из предложенных вариантов. В данном случае создается атмосфера свободных суждений и борьбы мнений, в которой вырабатывается умение решать задачу.