В настоящее время особую актуальность приобрели проблемы строительства новых и реконструкции существующих объектов в районах распространения слабых водонасыщенных грунтов, что обусловлено особенностью современного развития нефте- и газодобывающих районов Казахстана. При этом возникают не только технологические трудности, связанные с производством работ в особых условиях распространения слабых грунтов, но и повышенные требования к проектным решениям в этой области, как на стадии конструирования, так и во время расчета. Строительство новых высотных сооружений и их эксплуатация сопряжены со значительными затратами ресурсов. В целом проблема является весьма многогранной и, в частности, связана с использованием в основании таких конструкций глинистых водонасыщенных грунтов, для которых свойственны рыхлость, малая плотность и способность разжижаться при нарушении структуры из-за содержания воды, развития пластических деформаций сдвига, многократного промерзания-протаивания в процессе эксплуатации. В связи с этим исследование несущей способности водонасыщенного глинистого грунта в основании сооружений в процессе фильтрационной консолидации является актуальной геотехнической проблемой, имеющей существенное практическое значение и определяющей, в значительной степени, эффективность капитальных вложений, надёжность и нормальную эксплуатацию сооружений.
При проектировании фундаментов промышленных и гражданских сооружений, расположенных на слабых водонасышенных глинистых грунтах всегда надо иметь в виду, чтобы осадка по абсолютной величине была меньшей, чем это допускается и разность этих осадок должна быть крайне минимальной. Однако это не всегда удается выполнять. В большинстве случаев при строительстве сооружений на таких водонасыщенных глинистых грунтах, прежде чем строить высотные здания создают искусственные основания, применяя песчаные подушки мощностью от 1-2 м до 7 м. Они позволяют уменьшить глубину заложения фундаментов и увеличивают их устойчивость, а также применение их уменьшает осадки фундаментов. Кроме того, песчаные подушки используются в качестве дренирующего слоя, так как поровая вода из нижележащих водонасыщенных глинистых грунтов отжимается в процессе уплотнения грунтов от веса самой подушки, ускоряя процесс консолидации грунтов основания. К большому сожалению, существующие методы расчета консолидации слабых водонасыщенных глинистых грунтов имели невысокую точность. Видимо, это связано с некоторыми неучтенными явлениями, происходящими в грунтах. В частности, от величины структурной прочности сжатия, ползучести и от неоднородности самого грунта.
В связи с этим в данной работе допущено, что для сильно сжимаемых водонасыщенных глинистых грунтов в начальный момент времени часть нагрузки, мгновенно приложенной нагрузки q к грунту, равная по величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта [1], т.е.
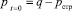 . (1)
. (1)
Как известно, верхняя часть земной коры обычно характеризуется высокой степенью неоднородности слагающих ее грунтов и пород. Это обусловлено достаточно сложным геолого-тектоническим строением пород, на которых строится тот или иной строительный объект. Не учет неоднородностей геологического строения верхней части земной коры может привести в будущем к повреждениям инженерных сооружений, вследствие осадки, развития в основании фундаментов. Обычно неоднородность грунта определяется через его гранулометрический (зерновой) состав. А гранулометрический состав грунта следует определять по весовому содержанию в нем частиц различной крупности, выраженному в процентах по отношению к весу сухой пробы грунта, взятой для анализа. В данной же работе для теоретического исследования процесса уплотнения неоднородного грунта модуль его деформации математически выражается через экспоненциальную функцию, которая изменяется по глубине уплотняемого грунтового массива по закону [5]
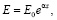 (
(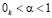 ), (2)
), (2)
где E0, α – опытные данные. Попов Г.Я. в этой работе такую неоднородность грунта использовал при решении контактных задач теории упругости. Такая неоднородность грунта также учтена в работах [3, 4].
Кроме того, по своей природе глинистые грунты относятся к реологическим телам. Это свойство находит свое выражение в медленной, длительно не затухающей деформации грунтовых оснований. Эти деформации, связанные с явлением ползучести, находят свое выражение в оседании земляных масс с некоторыми незначительными скоростями. Однако, несмотря на такую, казалось бы, незначительную интенсивность деформации, они в ряде случаев могут оказаться недопустимыми для сооружений, расположенных на деформируемых основаниях. Также заметим, что здания, во многих случаях довольно хорошо воспринимающие даже значительные вертикальные деформации, в результате их неравномерной осадки приводятся разрушению. Такие медленные деформации, связанные с ползучестью глинистых грунтов, в некоторых случаях оказываются очень опасными. Такое свойство неоднородных водонасыщенных грунтов в данной работе подчиняется теории упругоползучего тела Г.Н. Маслова, Н.Х. Арутюняна [2]. Тогда основная зависимость между коэффициентом пористости 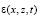 и суммой главных напряжений
и суммой главных напряжений 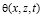 в интерпретации В.А. Флорина [6] для неоднородной уплотняемой среды может быть представлена в виде:
в интерпретации В.А. Флорина [6] для неоднородной уплотняемой среды может быть представлена в виде:
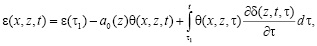 (3)
(3)
Здесь
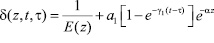 , (4)
, (4)
где E(z) – модуль общей деформации, зависящий от координаты z; a1, g – параметры ползучести; 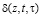 – относительная деформация от единичной силы; a0(z) – коэффициент сжимаемости для неоднородного уплотняемого грунта. Он зависит от координаты z, т.е. от глубины расположения исследуемой точки.
– относительная деформация от единичной силы; a0(z) – коэффициент сжимаемости для неоднородного уплотняемого грунта. Он зависит от координаты z, т.е. от глубины расположения исследуемой точки.
Как известно, для практики интересен случай уплотнения многофазных грунтов конечной глубины, где может находиться водонепроницаемый слой. Кроме того наличие ограничивающих стенок может иметь самостоятельный интерес. В связи с этим, рассмотрим процесс уплотнения грунтового прямоугольника длиной 2l, толщины h, имеющего водонепроницаемые ограничивающие стенки по бокам и водонепроницаемый слой на глубине h. Пусть при этом на некоторой части (-а а) верхней поверхности этого прямоугольника в момент времени t=τ1 приложена распределённая нагрузка с интенсивностью q(x,z,t). Тогда математическая постановка данной задачи заключается в следующем: требуется определить в этом массиве распределение давлении в поровой жидкости р(х,z,t), напряжение в скелете упругоползучего грунта 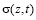 и вертикальные перемещения точек верхней поверхности S(t) (осадок). При этом основное уравнение механики уплотняемых водонасыщенных глинистых грунтов, обладающих свойствами неоднородности и ползучести имеет вид:
и вертикальные перемещения точек верхней поверхности S(t) (осадок). При этом основное уравнение механики уплотняемых водонасыщенных глинистых грунтов, обладающих свойствами неоднородности и ползучести имеет вид:
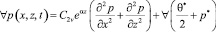 , (5)
, (5)
где ∀ – интегро-дифференциальный оператор вида:
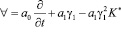 , (6)
, (6)
Уравнение (5) при (6) решается в определенных граничных и начальных условиях. Причем, если учесть устройство песчаной подушки под фундаментом сооружений, то граничные условия для указанной исследуемой задачи относительно порового давления р(x, z, t) будут:
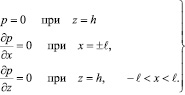 (7)
(7)
Чтобы определить давление в поровой жидкости, соответствующее начальному моменту времени необходимо решать следующее дифференциальное уравнение
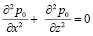 . (8)
. (8)
Решение уравнения (8), если учесть выражение (1), должно удовлетворять следующим неоднородным граничным условиям:
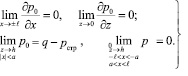 (9)
(9)
Уравнение (8) при граничных условиях (9) имеет решение вида:
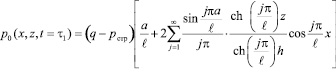 . (10)
. (10)
Здесь следует заметить, что
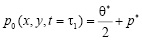 ,
,
где 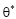 и p* величины определяют значения соответственно суммы главных напряжений и порового давления для стабилизированного состояния уплотняемого массива.
и p* величины определяют значения соответственно суммы главных напряжений и порового давления для стабилизированного состояния уплотняемого массива.
Теперь определим решение задачи для не стабилизированного состояния грунтового прямоугольника. Для этого решим краевую задачу (5) при (7), (9), Это решение получится в виде
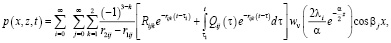 (11)
(11)
где функция 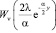 , входящая в выражение (11) для целого индекса
, входящая в выражение (11) для целого индекса 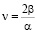 имеет вид
имеет вид
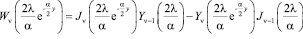 ; (12)
; (12)
для дробного индекса эта функция вычисляется по формуле
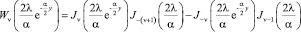 ; (13)
; (13)
функции 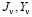 являются функциями Бесселя первого и второго родов.
являются функциями Бесселя первого и второго родов.
Параметр l для целого индекса n находится из равенства
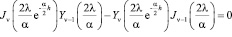 . (14)
. (14)
Уравнение (9) для дробного индекса ν будет представлено в виде:
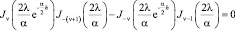 . (15)
. (15)
Произвольные постоянные Rijk и величина Qijk, входящие в (11) определяются из следующих соотношений:
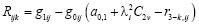 . (16)
. (16)
Здесь
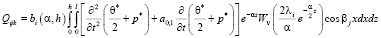 ; (17)
; (17)
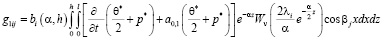 ; (18)
; (18)
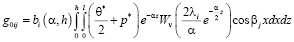 . (19)
. (19)
Выражение (11) при (12)-(19) дает возможность для конечной области уплотнения, находящейся под действием распределенной нагрузки, изменяющейся произвольным законом вычислить изменение порового давления для любого момента времени в зависимости от пространственных координат. При этом сумму главных напряжений находим из выражений:
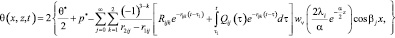 . (20)
. (20)
Тогда осадку уплотняемого грунтового массива в виде прямоугольника можно представить так:
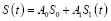 , (21)
, (21)
где
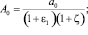
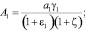
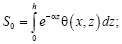
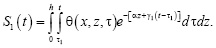 (22)
(22)
Теперь рассмотрим тот случай, когда на поверхность уплотняемого слоя грунта модуль деформации которого изменяется по глубине приложена равномерно распределенная нагрузка. Для этого случая распределение порового давления согласно (11) имеет вид:
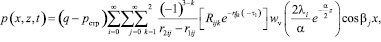 (23)
(23)
так как величина Qijk, входящие в (23) равна нулю. Здесь 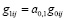 . Величина g0ij вычисляется по формуле (19).
. Величина g0ij вычисляется по формуле (19).
Нетрудно убедиться в том, что выражение (23) удовлетворяет всем краевым условиям задачи. Причем из этого соотношения имеем, что
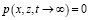 .
.
Тогда как при 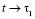 , находим
, находим
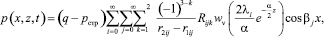 . (24)
. (24)
Следовательно, поровое давление для исследуемого случая изменяется в пределах от
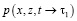 ,
,
определяемое формулой (24) до нуля.
Осадку слоя грунта можно определить формулой (21). При этом имеем:
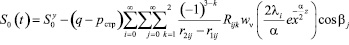 ;
;
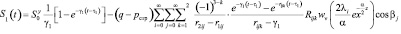 . (25)
. (25)
Таким образом, использовав соотношения (24), (25) можно определить значения порового давления и осадок уплотняемого неоднородного грунтового массива в виде прямоугольника, обладающего свойством ползучести.
Следует заметить, что все решения исследуемой задачи получены в виде комбинации бесселевых функции. Эти функции в настоящее время достаточно хорошо исследованы и имеют числовые значения для любого порядка. Следовательно, определения числовых значений порового давления, напряжения в скелете грунта и вертикальных перемещений не представляют трудности.




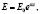 (
(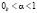 ). Popov G.Ya. used such king of the earth heterogeneity at solution of contact problems of theory of elastic strength. Besides, in the work it is accepted that for tightly compressible water-saturated clay ground in the initial time point the part of weighting, immediately applied weight q to earth, equal to the structural compressive strength of solution, is right away perceived by soil skeleton, i.е.
). Popov G.Ya. used such king of the earth heterogeneity at solution of contact problems of theory of elastic strength. Besides, in the work it is accepted that for tightly compressible water-saturated clay ground in the initial time point the part of weighting, immediately applied weight q to earth, equal to the structural compressive strength of solution, is right away perceived by soil skeleton, i.е. 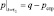 . Calculation formula for estimation of the porous pressure values, sum of main stress and settlement of compatible earth square having properties of creeping and heterogeneity has been obtained in the work on the basis of that statement of consolidation problem.
. Calculation formula for estimation of the porous pressure values, sum of main stress and settlement of compatible earth square having properties of creeping and heterogeneity has been obtained in the work on the basis of that statement of consolidation problem.