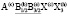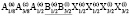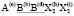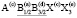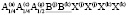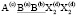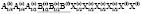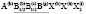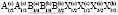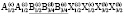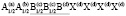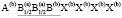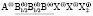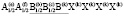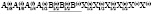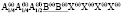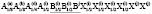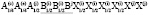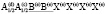Для семейства кристаллов со структурой шпинели характерен очень широкий спектр различных физических и химических свойств, открывающих значительные возможности для важных применений [1-7]. Многие свойства шпинелей существенно зависят от упорядочения атомов в их структуре [8-23]. В этой статье мы рассмотрим возможные типы упорядочения атомов (возможные сверхструктуры) в октаэдрических позициях структуры шпинели. Ранее уже проводилось исследование катионного упорядочения в октаэдрических узлах шпинели [24]. Простой геометрический перебор возможных сверхструктур с порядком типа 1:1 в октаэдрической подрешетке шпинели привел к 12870 вариантам [24]. Если ограничиться только изучением ячеек, содержащих центрированные грани, то останется только 198 случаев. Авторы [24] обсуждают возможности реального существования этих сверхструктур и после ряда предположений физического характера пришли к выводу о существовании двух сверхструктур с порядком 1:1 в октаэдрической подрешетке шпинели. Нами использован теоретико-групповой метод термодинамической теории фазовых переходов, детально описанный в [25-37]. Нами получены результаты, существенно отличные от выводов, полученных в [24].
Представление упорядочения, построенное на позиции 16(d) имеет размерность 52. Оно состоит из следующих неприводимых представлений
k 8(τ1+τ2) + k9(τ1+t4+t5) +k10(τ1+τ3)+k11(τ1(A1g) + t7(F2g)) (1)
Обозначения волновых векторов и неприводимых представления даны по книге О.В. Ковалева [38]. Приводимый параметр порядка (ПП) (1) генерирует 320 низкосимметричных упорядоченных фаз, включая фазу, индуцированную единичным представлением k11τ1(A1g). Среди этих фаз имеется 6 бинарных (фазы 1-6) и 9 тройных (фазы 7-15) сверхструктур (таблица). Так же, как и в подрешетке 8(a), такие упорядоченные структуры могут быть описаны ПП, преобразующимся по одному неприводимому представлению.
Упорядочение в бинарных сверхструктурах происходит по типам 1:1 и 1:3, а тройных – по типам 1:1:6, 2:3:3 и 1:1:2. Среди возможных сверхструктур имеются четыре пары энантиоморфных модификаций упорядоченных шпинелей.
Наиболее распространенными типами катионного упорядочения в позициях 16(d) шпинели являются структуры с пространственными группами P41(3)22 (параметр порядка (0, 0, 0, 0, 0, j), k10τ1), P43(1)32 (параметр порядка (0, j, 0, j, 0, -j), k10τ1) и Ibmm (параметр порядка (0, x, 0), k11(t7)).
Бинарное и тройное катионное упорядочение в вайковой позиции 16(d) структуры шпинели
|
№ п/п |
Параметры порядка |
Символ пространственной группы |
V’/V |
Трансляции примитивной ячейки |
Структурная формула |
|
1 |
(x, -x, x)7 |
D3d5=(N166) |
1 |
a1, a2, a3 |
|
|
2 |
(j, 0, j, 0, j, 0)3 |
Td1=(N215) |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
3 |
(0, x, 0)7 |
D2h28= Immа (N74) |
1 |
a1, a2, a3 |
|
|
4 |
(0, j, 0, j, 0, -j)1 |
O6=P4332(N212) O7=P4132(N213) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
5 |
(0, j, 0, 0, 0, 0)3 |
D2d5=(N115) |
2 |
a1+a3, a2, 2a1 |
|
|
6 |
(0, 0, 0, 0, 0, j)1 |
D43=P4122(N91) D47=P4322(N95) |
2 |
a2+a3, 2a2, a1 |
|
|
7 |
(0, j, 0, 0, j, 0)1 (0, 0, 0, j, 0, 0)3sec. |
D2d3=(N113) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
8 |
(0, 0, j, j, 0, 0)1 (0, x, 0)7sec. |
D2h7=Pbmn(N53) |
2 |
a1+a3, a2, 2a1 |
|
|
9 |
(0, 0, h, 0)4(x, -x, x)7sec. |
D3d5=(N166) |
2 |
a1, a3, 2a2 |
|
|
10 |
(0, 0, h, 0)1(x, -x, x)7sec. |
D3d5=(N166) |
2 |
a1, a3, 2a2 |
|
|
11 |
(j, 0, 0, 0, 0, -j)3 (0, 0, j, 0, 0, 0)1sec. |
D43=P4122(N91) D47=P4322(N95) |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
12 |
(0, ϕ1, 0, ϕ2, 0, -ϕ1)1 |
D44=P41212(N92) D48=P43212(N96) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
13 |
(ξ1, -ξ1, ξ2)7 |
C2h3=C2/m(N12) |
1 |
a1, a2, a3 |
|
|
14 |
(j, j, 0, 0, 0, 0)3 (0, 0, x)7sec. |
D2h5=Pcmm(N51) |
2 |
a1+a2, a3, 2a1 |
|
|
15 |
(ϕ1, 0, ϕ2, 0, -ϕ2, 0)3 |
D2d1=(N111) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
16 |
(0, 0, q, q, 0, 0, 0, 0, 0, 0, 0, 0)1 |
D2d12= (N122) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
17 |
(0, 0, 0, 0, 0, 0, q, 0, 0, 0, 0, 0)1 (j, 0, 0, 0, 0, 0)3sec. |
D2d11= (N121) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
18 |
(0, q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)2 (0, j, 0, 0, 0, 0)3sec. |
D2d11= (N121) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
19 |
(0, 0, q, q, 0, 0, 0, 0, 0, 0, 0, 0)2 |
D2d12= (N122) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
Примечание. Обозначения для ПП: k8 – q, k9 – h; k10 – j, k11 – x. Верхний индекс после круглой скобки – номер представления по Ковалеву [38], V’/V – изменение объема примитивной ячейки в результате структурного фазового превращения. Верхний индекс в стехиометрической формуле – обозначение типа позиции по интернациональным таблицам.
Особенностью строения упорядоченных энантиоморфных P4122- и P4322- фаз, а также P4332- и P4132- фаз является то, что среди элементов симметрии пространственной группы её структуры нет инверсии и плоскостей симметрии, а есть только оси симметрии. Такие кристаллы могут существовать в правой и левой модификациях, являющихся зеркальными отражениями друг друга. По физическим свойствам они не различимы (исключая оптическую активность). В кристаллах LiFe5O8 они существуют в одном образце как различные домены [39].
Структуры упорядоченных шпинелей с энантиоморфными пространственными группами P4122 и P4322. Эти структуры образуются в результате фазового перехода с критическим параметром порядка, преобразующимся по шестимерному НП k10τ1. Упорядочение катионов типа 1:1, расположенных в октаэдрических позициях структуры кубической шпинели, сопровождается смешениями тетраэдрических и октаэдрических катионов, а также смещениями анионов. В низкосимметричной фазе упорядочиваются и анионы (тип порядка 1:1). Структурная формула низкосимметричной фазы А4(с)В4(а)В‘4(в)Х8(d)2Х8(d)2. Структуру P41(3)22-фаз имеют LiZnNbO4, Li2TeO4, A2TiO4 (где A=Zn, Mn, Mg); Zn2GeO4 ), LiMnNbO4, Zn0.8Co1.2GeO4.
Структуры упорядоченных шпинелей с энантиоморфными пространственными группами P4132 и P4332. Это один из наиболее распространенных типов упорядоченных шпинельных структур. Критическое НП k10τ1. входит как в перестановочное (на позициях 16(d) и 32(е)), так и в механическое (на позициях 8(а), 16(d), 32(е)) представления кристалла и поэтому понижение симметрии кристаллов обусловлено смещениями всех типов атомов и упорядочениями октаэдрических катионов и анионов. В низкосимметричной фазе упорядочиваются октаэдрические катионы и анионы (тип порядка 1:3 в обоих случаях). Структурная формула низкосимметричной фазы А8(с)2В4(в)В12(d)3Х8(c)2Х24(е)6. Cтруктуру упорядоченной P43(1)32 (O6(7))-фазы имеют модификации LiM5O8 (M=Al, Ga), Zn3Ni2TeO8, Zn2Co3TeO8, CuMg0.5Mn1.5O4, Cu1.5Mn1.5O4, Zn2Mn3O8, ZnMGe3O8 M=Mn, Mg, M2Ge3O8 M=Zn, Co, ZnMTi3O8 M= Mn, Cd, M2Ti3O8 M=Zn, Mn, Co, V2Co3O8, Li2Mn3CoO8, Li0.5+0.5xFe2.5-1.5xTixO4 (0³ x ³ 0.4, 1.2 ³ x ³ 1.57), Na4Ir3O8, LiMnTiO4, Na4Sn3O8, LiNi0.5Mn1.5O4, LiFe5−xMnxO8 (0≤x≤1), LiFe5O8, LiMg0.1Ni0.4Mn1.5O4, LiNi0.5Mn1.5O4-d, LiNi0.5Mn1.5O4, Li1.25Fe0.25Ti1.5O4, Li2Mn3MO8 (M=Mg, Zn), LiMg0.5Mn1.5O4, CuMg0.5Mn1.5O4, LixMg1-2xFe2+xO4 x ³ 0.40, LiMgxMn2-xO4 (x>1), Li2CoTi3O8, Li2Zn3O8, Li2Ge3O8, LiM0,5Ti1,5O4, LiM0,5Ge1,5O4 (M=Mg, Co, Ni, Zn), Li1.33xCo2−2xTi1+0.67xO4, Li1−0.5xFe2.5xMn2−2xO4, LiMn2−y TiyO4 (y>1), LiFe0.5Ti1.5O4 и другие.
Структура упорядоченной шпинели с пространственной группой Immа. Критическое НП k11t7 входит в механическое представление кристалла на позициях 8(а) и 32(е) и в перестановочное представление на позициях 16(d) и 32(е). Следовательно, низкосимметричная модификация Immа-фазы образуется в результате смещений тетраэдрических катионов и анионов, а также упорядочения октаэдрических катионов и анионов (в обоих случаях образуется порядок типа 1:1). Структурная формула низкосимметричной фазы А4(e)В4(a)В‘4(d)Х8(h)2Х8(i)2. Структуру упорядоченной Immа -фазы имеют низкосимметричные модификации шпинелей Li2CoCl4, Li2MnBr4, Li2MgBr4, LiVCuO4,
Li1-xCuVO4 (0≤x≤0.2), LiSbZnO4, Li2FeCl4.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки № 6.8604.2013.