Среди известных методов количественного газохроматографического анализа [9] метод стандартной добавки (СД) характеризуется уникальными возможностями. Для определения суммарного количества аналита (Мх) анализируют исходный образец до и после добавки известного количества образца сравнения (Мдоб):
Мх = Мдоб Sx / (Sx+доб – Sx) = Мдоб / (Sx+доб/Sx – Sx), (1)
где Sx и Sx+доб – площади пиков определяемого компонента до и после добавки.
Только этот способ позволяет определять суммарное количество целевых аналитов в гетерофазных системах по результатам анализа только одной из сосуществующих фаз (обычно выбирают ту, которая содержит меньшее количество мешающих веществ) [2, 3, 6]. Кроме того, как было недавно показано, он применим в условиях нелинейности детектирования, когда возможности других методов ограничены [4, 6-8], а также при недостаточной инертности хроматографических систем по отношению к определяемым компонентам. Стандартный вариант метода, основанный на соотношении (1), в подобных случаях неприменим; необходимо использование нескольких последовательных стандартных добавок, Мдоб(i) = SМдоб(1 ≤ k ≤ i):
Мх(i) = Мдоб(i) Sx / (Sx+доб(i) – Sx) = Мдоб(i) / (Sx+доб(i)/Sx – Sx). (2)
В результате получаем совокупность нескольких значений определяемой величины Мх(i), соответствующих числу введенных добавок. Если все они одинаковы в пределах стандартных отклонений,
Мх(1) ≈ Мх(2) ≈… ≈ Мх(i),
то результат определений может быть получен их простым усреднением [5]. Если же наблюдается отчетливо выраженная зависимость определяемого количества от массы добавки, Мх = f(Мдоб), то необходима дополнительная обработка величин Mx(i), заключающаяся в оценке значений Мх, экстраполированных либо на нулевую добавку (Мдоб → 0), либо, как впервые показано в работах [4, 6-8], на ее бесконечно большую величину (Мдоб → ∝). Следовательно, расширение областей применения метода СД связано с решением двух достаточно «необычных» для химии и хроматографии математических задач:
1. Располагая набором данных {Sx+доб(i) ÷ Мдоб(i)} при условии Mx(i) ≠ const выбрать «направление» экстраполяции (Мдоб → 0 или Мдоб →∝);
2. Выбрать функцию для вычисления экстраполированных значений.
Возможности решения первой задачи проанализированы в статье [7]. Настоящая работа посвящена обсуждению второй проблемы. Обсуждаемые ниже примеры определения различных соединений в разнообразных матрицах методом последовательных СД подробно охарактеризованы в публикациях [4, 6-8].
Результаты и их обсуждение. Наиболее часто встречающимся в аналитической практике простейшим вариантом обработки результатов, полученных методом последовательных СД, является их экстраполяция на нулевые величины добавок в соответствии с уравнением линейной регрессии:
Мх = aМдоб + b, lim(Mx)|(Мдоб→ 0) = b (3)
Однако при решении различных аналитических задач встречается необходимость «альтернативной» обработки данных с их экстраполяцией на бесконечно большие величины добавок. В этом случае использование уравнения (3) невозможно, так как аппроксимирующая функция должна иметь предел при Мдоб →∝. Простейшей функцией, удовлетворяющей этому требованию, является двухпараметровая гиперболическая зависимость, выбранная для этих целей в работах [4, 6-8]:
Мх = a/Мдоб + b, lim(Mx)|(Мдоб →∝) = b (4)
Графическая иллюстрация этого варианта экстраполяции приведена на рисунке, а результаты вычислений экстраполированных значений сопоставлены с заданными содержаниями аналитов в таблице. В 12 случаях из 14 линейная [уравнение (1)] либо гиперболическая [уравнение (2)] экстраполяция обеспечивает точность в пределах ±15 % отн.
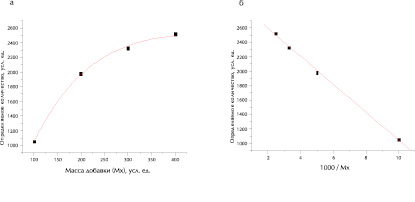
Схематическая иллюстрация экстраполяции результатов определений методом последовательных стандартных добавок на бесконечно большую величину добавки (Мдоб →∝): а – исходная нелинейная зависимость Мх = f(Мдоб); б – зависимость Мх = a(1000/Мдоб) + b, lim(Mx)/(Мдоб →∝) = b
Сравнение результатов количественного анализа методом последовательных стандартных добавок с использованием различных способов экстраполяции
|
Анализируемый образец |
Исходные данные, Mх(Мдоб) |
Экстраполирующая функция |
Мэкстраполир* |
Заданное содержание аналита** |
Логистическая регрессия*** |
|
1. Тест-смеси для области отсутствия инертности хроматографических систем |
17.94(17.5), 18.89(35)****, 18.26(52.5), 18.08(70) |
Гиперболическая (→ ∞) |
17.9 |
17.5 мкг/мл |
18.3(3); 18.4(4) [0.1] |
|
2. То же |
26.51(20.5), 25.69(41), 24.76(61.5), 24.12(82) |
Гиперболическая (→ ∞) |
23.7 |
25 мкг/мл |
25.3(3); 25.3(4) [0.1] |
|
3. То же |
43.0(35), 40.9(52.5), 33.5(70), 31.8(87.5) |
Гиперболическая (→ ∞) |
25.0 |
17.5 мкг/мл |
37.3(3); 37.3(4) [0.1] |
|
4. То же |
79.79(50), 73.03(75), 58.51(100), 42.69(125) |
Гиперболическая (→ ∞) |
27.0 |
25 мкг/мл |
63.7(3); 63.7(4) [0.001] |
|
5. То же |
16.97(19), 17.07(38), 17.09(57), 15.7(76), 15.48(95) |
Линейная (→ 0) |
17.8 |
19 мкг/мл |
4.8(3); 16.5(4) [0.1] |
|
6. То же |
15.77(12.5), 13.1(25), 12.63(37.5), 11.72(50), 13.57(62.5) |
Гиперболическая (→ ∞) |
10.6 |
12.5 мкг/мл |
13.4(3); 13.4(4) [0.1] |
|
7. Гидрофобный аналит в гидрофобной матрице [3] |
5.8(8.73), 6.2(17.46), 6.2(26.19), 6.4(34.92) |
Гиперболическая (→ ∞) |
6.5 |
8.8 мг |
6.4(3); 8.3(4) [0.01] |
|
8. Гидрофильный аналит в гидрофильной матрице [3] |
4.52(8.22), 5.43(16.44), 5.54(24.66), 5.46(32.88) |
Гиперболическая (→ ∞) |
6.0 |
6.5 мг |
5.5(3); 5.5(4) [0.01] |
|
9. 3-(2,2,2-Триметилгидразиний)пропионовая кислота (ТНР) в моче [3, 7] |
70.2(200), 69.3(300), 57.9(400), 57.3(500) |
Гиперболическая (→ ∞) |
48.8 |
50 мкг/мл |
63.7(3); 63.7(4) [0.01] |
|
10. То же |
726(100), 634(200), 623(300) |
Гиперболическая (→ ∞) |
563 |
600 мкг/мл |
660(3); 779(4) [1] |
|
11. То же |
672(100), 563(200), 500(300) |
Гиперболическая (→ ∞) |
427 |
400 мкг/мл |
747(3); 681(4) [1] |
|
12. Камфора в мазях [6] |
76(27), 50(55), 47(85) |
Линейная (→ 0) |
85.2 |
90 мг |
2.1(3); 58(4) [0.01] |
|
13. Моноэтаноламин в водных растворах [4] |
0.23(0.375), 0.35(0.875) |
Линейная (→ 0) |
0.14 |
0.125 мкг/мл |
0.126(3); 0.111(4) [1] |
|
14. То же |
1.88(1.0), 1.84(2.0) |
Линейная (→ 0) |
1.92 |
2.0 мкг/мл |
1.86(3); 1.86(4) [1] |
*) Жирным шрифтом выделены экстраполированные значения, совпадающие с заданным содержанием аналитов в пределах ± 15 %; **) масса (мг) или концентрация (мкг/мл); ***) в круглых скобках – число параметров логистической регрессии (3 или 4), в квадратных – коэффициент масштабирования независимой переменной; ****) курсивом выделены значения, исключенные при линейной или гиперболической экстраполяции.
Тем не менее, для лучшего понимания и обоснования возможностей метода последовательных СД целесообразно рассмотрение вопроса, можно ли описать оба варианта экстраполяции данных (Мдоб→0 и Мдоб →∝) одним и тем же регрессионным уравнением. При этом число параметров уравнения не должно быть чрезмерно большим, чтобы не увеличивать объем экспериментальной работы (число добавок). В связи с этим представляет интерес анализ возможностей логистической регрессии.
Логистическая регрессия может быть описана следующим известным нелинейным четырехпараметровым соотношением:
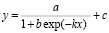, (5)
В уравнении трехпараметрового варианта логистической регрессии отсутствует свободный член (коэффициент с). Коэффициенты c и a иногда называют параметрами смещения и масштаба соответственно. Если они известны, то можно ввести новую безразмерную переменную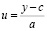 
, продифференцировать ее по x и, после исключения параметра b, получить однопараметровое нелинейное дифференциальное уравнение первого порядка:
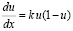. (6)
Подобное уравнение, известное как одно из уравнений химической кинетики, было использовано для описания автокаталитических реакций (конечный продукт является катализатором) [1]. В таких случаях в качестве независимой переменной x рассматривают время t, а зависимая переменная u представляет собой отношение концентрации конечного продукта в момент времени t к начальной концентрации (при t = 0) исходного реагента. Из уравнения (6) следует, что значение k/4 отвечает максимальной скорости процесса в момент времени t*, соответствующий точке перегиба зависимости u(х). Значение t* равно отношению ln(b)/k и поэтому параметры b и k уравнения (5) должны быть большими нуля.
В настоящей работе соотношение (5) и некоторые его частные формы, являющиеся решениями уравнения (6), использованы для обработки данных количественного газохроматографического анализа методом последовательных СД. Независимой переменной х, принимающей только положительные значения, будем считать массу стандартной добавки (Мдоб), в качестве зависимой переменной y можно рассматривать инструментальный отклик в виде площадей хроматографических пиков или, нагляднее, вычисленных на их основе по уравнению (2) содержаний аналита в исходной пробе (Мх). Массив экспериментальных данных можно представить как совокупность n пар переменных: (xi, yi), 1 ≤ i ≤ n. С использованием этого массива для нахождения значений параметров a, b, c и k соотношения (5) минимизировали целевую функцию W, представляющую собой сумму квадратов отклонений:
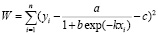. (7)
Кроме четырехпараметрового соотношения (5) использовали трех и двухпараметровые уравнения с дополнительными ограничениями (c = 0) и (c = 0, b = 1), соответственно.
Особый интерес для оценки возможностей применения приведенных выше уравнений для обработки данных, полученных методом последовательных СД, представляют предельные значения
y(x = 0) = a / (1 + b) + c. и y(x = ∞) = a + c.
Именно в интервал между этими значениями попадают экспериментально определяемые величины Mx(i) = f[Mдоб(i)], которые необходимо аппроксимировать обсуждаемой нелинейной зависимостью, характеризующейся точкой перегиба с координатами
y(x = ln(b)/k) = a/2 + c.
Вычисления проводили в среде Maple 14. Проверку полученных результатов осуществляли программным средством «Подбор параметров» электронных таблиц Microsoft Excel 2007. В качестве примера приведем фрагмент вычислений параметров a, b, c, k для примера № 7 в среде Maple 14 (после символа # приведены комментарии):
>M[доб]:=[8.73,17.46,26.19,34.92]:M:=[5.82,6.2,6.2,6.4]:
#исходные данные
> m:=map(x->x/100,M[доб]):#масштабирование переменной m[доб]
> zip((x,y)->(y-a/(1+b*exp(-k*x)- c)^2,m,M):W4:=add(i,i=%): #четырехпараметровая целевая функция
> with(Optimization):#библиотека команд оптимизации
> Minimize(W4,assume=nonnegative);#наименьшее значение целевой функции W4 и искомые значения параметров
W4 = 0.024, [a = 5.34, b = 0.96, c = 2.99, k = 1.56]
Предельное значение Mx при Mдоб → ∞ равно a + c = 8.33 (при заданном количестве аналита 8.8).
Общая сводка результатов оценки содержания аналитов в различных образцах методом последовательных СД с использованием логистической регрессии в сравнении с результатами, полученными линейной и гиперболической экстраполяциями, также приведена в Табл. 1. Соответствие вычисленных и экспериментальных данных в пределах ± 15 % наблюдается в девяти из 14 примеров, что несколько меньше, чем двумя другими методами. Однако важно отметить, что факты получения неудовлетворительных результатов (примеры № 3, 4, 9, 11 и 12) не только объяснимы, но и позволяют сделать важные заключения об изменении условий анализа методом последовательных СД. Математическим критерием неудовлетворительной логистической регрессии являются высокие значения целевой функции W [соотношение (7)] (примеры 9-12). Кроме того, невысокую точность экстраполяции можно ожидать в тех случаях, когда диапазоны вариаций значений Mx(i) чрезмерно велики [в примерах № 3, 4, 11 и 12 отношения (Mx(i)макс / Mx(i)мин) превышают 1.35]. В подобных случаях целесообразно изменить экспериментальные условия количественного анализа методом последовательных СД так, чтобы избежать столь существенных вариаций определяемых содержаний аналитов.
Применение метода стандартной добавки и его модификаций (вариант последовательных стандартных добавок) для количественного определения аналитов обеспечивает высокую точность результатов для образцов, отличающихся сложным характером матриц, в условиях нелинейности детектирования, а также в областях недостаточной инертности хроматографических систем. Однако реализация таких возможностей требует использования «нестандартных» алгоритмов интерпретации результатов, в том числе экстраполяции промежуточных содержаний аналитов на нулевую или бесконечно большую величины добавок. Показано, что для этих целей можно применять логистическую регрессию, характеризующуюся существованием двух пределов функции при стремящихся как к нулю, так и к бесконечности значениях аргумента.