Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Эксперименты в области передачи мыслей на расстоянии проводились в 1919-1927 гг. академиком Владимиром Бехтеревым в Ленинградском институте по изучению мозга. В 1929 г. он сделал доклад о результатах своей работы по мысленному воздействию между людьми на конференции Института мозга и психической деятельности. В это же время похожие опыты проводил инженер Б. Кажинский [2]. Советское правительство в 1932 г. поручило Ленинградскому институту мозга активнее взяться за экспериментальные исследования в области мыслепередачи, научное руководство было возложено на профессора Васильева. Соответствующий приказ получила и Лаборатория биофизики АН СССР, возглавляемая академиком П. Лазаревым. Начиная с 1958 года, многие крупные американские фирмы, известные своей продукцией в области электроэнергетики и электроники, организовали у себя исследовательские лаборатории по изучению эффекта передачи мыслей на расстоянии – фирмы Вестингауз, Дженерал Электрик, Бэлл Телефон и другие.

Опыты, проводившиеся в СССР и за рубежом, вроде бы подтвердили возможность передачи информации от одного человека к другому без использования каких либо технических средств. Однако, какова физическая природа явления и как практически использовать такой канал связи, по-прежнему остается неясным.

Мозговые ритмы. Попробуем вначале ответить на первый вопрос. Более полувека назад немецкий психиатр Ганс Бергер [6], изучая электрическую активность головного мозга человека, впервые обнаружил слабые колебания с частотой около 10 в секунду и назвал их альфа-ритмами. Их размах, или амплитуда, составляет всего около 30 миллионных долей вольта. Через 25 лет, изучение этих еле заметных волн выросло в новый раздел науки, ныне называемый электроэнцефалографией – ЭЭГ [1]. Кроме того, в человеческом мозге обнаружились и другие типы ритмов [4]:

– дельта-ритм (от 0.5 до 4 колебаний в секунду, амплитуда – 50-500 мкВ);

– тэта-ритм (от 5 до 7 колебаний в секунду, амплитуда – 10-30 мкВ);

– альфа-ритм (от 8 до 13 колебаний в секунду, амплитуда – до 100 мкВ);

– сигма-ритм – «веретена» (от 13 до 14 колебаний в секунду);

– бета-ритм (от 15 до 35 колебаний в секунду, амплитуда – 5-30 мкВ);

– гамма-ритм (от 35 до 100 колебаний в секунду, амплитуда – до 15 мкВ);

Альфа-ритм регистрируется у 85-95% взрослых здоровых людей. Лучше всего он выражен в затылочных отделах, а наибольшую амплитуду имеет в состоянии спокойного бодрствования, особенно при закрытых глазах и в затемненном помещении. Блокируется или ослабляется при повышении внимания (в особенности зрительного) или при мыслительной активности. Бета-ритм характеризует собой процесс обработки данных, включающий сотни мелких вычислений между двумя ближайшими областями коры. Когда мы начинаем испытывать сонливость, на ЭЭГ, прежде всего, наблюдается уменьшение интенсивности альфа-ритмов, свойственных состоянию бодрствования, и их постепенное замещение тэта-ритмами. У спокойно спящего человека доминируют медленные дельта-волны, хотя во время сна могут возникать несколько периодов быстрых колебаний – веретенообразных групп волн сигма-ритма с частотой около 14 колебаний в секунду – это спящий видит сны.

Из сказанного выше следует, что в состоянии бодрствования мозг реально способен генерировать и, по-видимому, принимать низкочастотные электромагнитные колебания порядка 8–35 Гц. Пропускная способность такого канала связи чрезвычайно низка, однако, надо заметить, не равна нулю. Другими словами, возможна передача лишь очень простых сигналов за сравнительно большое время, исчисляемое секундами или даже десятками секунд. Под простыми сигналами будем понимать 0 или 1, которые давно и успешно используются в вычислительной технике. Здесь следует подчеркнуть, что передача и прием мысленных сообщений требуют совершенно разных по способностям людей, а их подбор основан на специальной методике.

Алгоритм мысленной передачи сигналов. Проведем следующий простой эксперимент – попытаемся с помощью предварительно подобранного индуктора передать символ за символом случайную последовательность, составленную из десятка нулей и единиц, например, такую: 0 1 0 1 1 1 0 0 1 0. Задача перципиента – принять эту комбинацию также символ за символом, не ограничиваясь во времени. Одно замечание. Если заставить индуктора передавать несколько десятков нулей и единиц, а перципиента их принимать, то, скорее всего, быстро наступит усталость, в результате начнут появляться дополнительные ошибки никак не связанные с мыслепередачей. Чтобы в какой-то степени избежать этого, вместо нулей и единиц выберем и подготовим две похожие на них картинки, Например, вырезанный из бумаги зеленый круг диаметром 8 см. будет соответствовать нулю, а красная вертикальная полоска длиной 10 см. и шириной 1 см. – единице. И еще – для получения наилучшего результата необходимо выполнить ряд предварительных условий: сесть за стол так, чтобы было удобно и комфортно, успокоиться, отвлечься от всех посторонних мыслей, сконцентрироваться исключительно на поставленной задаче – видеть изображенные фигуры.

Рассмотрим теперь шаг за шагом процесс передачи и приема последовательности, которые в данном эксперименте осуществлялись на расстояние в несколько метров:

– индуктор и перципиент расходятся так, чтобы не видеть друг друга; у каждого имеются по две совершенно одинаковые картинки – зеленый круг и красная полоска;

– в соответствии с первым символом сообщения – нулем, индуктор кладет перед собой только круг, сообщая об этом перципиенту словом «начали» и предельно внимательно разглядывает его, стараясь спроектировать изображение в свое сознание; поверхность под кругом и рядом с ним должна быть чистой, ровной и без посторонних предметов;

– перед перципиентом лежат обе картинки – круг и полоска, на которые он смотрит попеременно и пытается определить, какая из них ему более благоприятна; сделав выбор, он сообщает индуктору сам или через посредника, что символ идентифицирован, например, произнеся слово «готово»;

– процесс продолжается до тех пор, пока не будут переданы и приняты все 10 символов.

В рассматриваемом нами примере перципиентом, в конце концов, была принята следующая последовательность нулей и единиц: 0 0 0 1 0 1 0 1 1 0. Если теперь сравнить их между собой, то обнаружится совпадение 7 символов. Подведем промежуточный итог. Проведенный простой эксперимент наглядно показал, что передача мыслей на расстояние реально существует, однако, по результатам одного опыта может возникнуть вполне законное сомнение – не является ли принятая комбинация случайной. Для того, чтобы его развеять, выполним трехкратный прием перципиентом одной и той же последовательности, после чего, для повышения достоверности принятой информации, воспользуемся методом накопления [5]. Результаты опыта оформим в виде таблицы (табл. 1).

Таблица 1

Реализация трехкратного накопления

Символ суммы формируется в зависимости от того, какого символа окажется больше в соответствующем столбце, например, в первом – два нуля и одна единица, в Сумму пишем – 0; во втором столбце оказалось наоборот – две единицы и один нуль, следовательно, в ячейку Сумма запишем 1 и т.д. Чтобы исключить неопределенность при определении сумм, количество опытов должно быть нечетным. В правом столбце указаны вероятности приема перципиентом последовательностей и результирующая вероятность.

Передача изображений. В качестве простейших изображений удобнее всего использовать карты Зенера [3], которые представляют собой набор из пяти рисунков, предложенный в 1930-х годах психологом Карлом Зенером для экспериментов с парапсихологическими явлениями. Такие карты широко используются на практике.

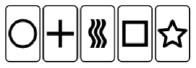
Рис. 1. Карты Зенера

Для людей со средними способностями распознавание карт Зенера – это такая же сложная задача, как и прием обычных картинок и фотографий. Именно этим обстоятельством можно объяснить большое число неудачных опытов по мысленной передаче сообщений, о которых немало сказано в печати.

Покажем, что любую карту, из представленных выше, можно передать, а затем идентифицировать на приеме, используя изложенную выше методику. С этой целью одну из карт вначале закодируем таким образом, чтобы привести в соответствие передаваемую информацию (карту Зенера) и низкоскоростной канал связи. Известно [5], что любое сообщение – звук, текст, рисунок, передаваемое с помощью технических средств связи, может быть представлено двоичным кодом. Выберем для передачи картинку круг, закодируем ее нулями и единицами и получим следующую матрицу кодов, которую для удобства дальнейшего анализа снабдим координатами – строки обозначим латинскими буквами (a, b, c, d, e), а столбцы – цифрами (1, 2, 3, 4, 5).

Таблица 2

Кодирование карты «круг»

Далее, чтобы полностью исключить угадывание, будем передавать ее не по 5 символов, как они расположены в матрице, а по 10, т.е. по две строки подряд (например, a,b c,d e,a … ). Кроме того, исходную карту круг будем передавать последовательно семь раз – это позволит в дальнейшем реализовать метод накопления, с помощью которого мы попытаемся увеличить четкость принятого изображения до приемлемого уровня. В результате получим 18 кодовых групп символов для передачи.

Таблица 3

Двоичные последовательности для передачи индуктором

Индуктор, держа перед собой таблицу, одну за другой передает последовательности a,b c,d e,a … символ за символом (заметим, что слово передает, здесь пишется без всяких кавычек). Передача идет в несколько приемов, дабы исключить возможные ошибки от усталости и других случайных факторов. Перципиент, приняв одну строку, например, a,b, передает ее посреднику и переходит к приему следующей – c,d. Таким образом, исключается возможность сравнения только что принятой последовательности с предыдущими. В итоге перципиентом получены следующие результаты:

Таблица 4

Принятые перципиентом двоичные последовательности

Далее, разобьем эту таблицу на пять частей – в соответствии с количеством исходных строк (a, b, c, d, e). Иначе говоря, в первую часть будем переносить коды, обозначенные в таблице 4 буквой a, во вторую часть – коды, обозначенных буквой b и так далее, до e. В каждой из пяти частей затем последовательно реализуем метод накопления – сначала трехкратный, затем пятикратный и, наконец, семикратный. Например, для строк, обозначенных буквой b, будем иметь:

Таблица 5

К реализации накопления для строк b

В качестве первого шага рассмотрим прием без накопления, который получится, если взять информацию откуда-нибудь из середины таблицы 4, например, из строк 6, 7 и 8. Тогда изображение закодированного круга будет иметь вид (здесь координаты можно опустить):

Таблица 6

Прием без накопления

Даже в этом простейшем случае ошибочно принятых символов оказалось всего 6 (они подчеркнуты), что соответствует вероятности правильного приема равной

p = 19/25 = 0.76.

Из рисунка пока не ясно, изначально передавался круг или квадрат, поэтому воспользуемся методом трехкратного накопления символов. Это значит, что одну и ту же исходную матрицу индуктор будет передавать трижды, что соответствует строкам 1–8 табл. 3. После приема названных строк перципиентом, каждый элемент матрицы будет выбираться из трех, аналогично тому, как это было во втором примере. Тогда получим:

Таблица 7

Трехкратное накопление

Исходное изображение принято с меньшими искажениями, а именно, из 25 переданных символов, правильно принято 20 и соответственно р = 20/25 = 0.8. В табл. 7 более четко просматриваются элементы круга. Действительно, в трех углах нули, а по границам матрицы в основном единицы.

Для дальнейшего улучшения изображения реализуем метод пятикратного накопления – теперь индуктор должен передать первые 13 строк кодов, которые после их приема перципиентом и последующего пятикратного суммирования дадут матрицу:

Таблица 8

Пятикратное накопление

Неправильно принято только 4 символа из 25, следовательно, р = 21/25 = 0.84. Посмотрим на полученный рисунок и сравним его с оригиналом. Можно заметить, что они практически совпадают, т.е. его нельзя перепутать, например, с квадратом или крестом, а тем более со звездой или волнистой линией.

Зададимся вопросом, можно ли и дальше улучшать изображение, увеличивая количество переданных исходных матриц, например, до семи. Для этого случая потребуется передача индуктором всех 18 последовательностей, их приема перципиентом с последующей реализацией семикратного накопления символов. В результате всего этого получим:

Таблица 9

Семикратное накопление

Теперь правильно приняты 24 символа из 25 и, таким образом р = 24/25 = 0.96. Совершенно очевидно, что увеличение количества переданных изображений исходной матрицы с последующей реализацией на приеме метода накопления, дает все более четкую картинку, демонстрируя высокую эффективность мыслепередачи.

Передача текстов. Теперь будет интересно посмотреть, как поведет себя рассмотренный выше метод применительно к текстам. И здесь, как представляется, есть одна проблема, которую желательно проверить. Дело в том, что ошибки, неизбежно возникающие в процессе мысленной связи, могут иметь разные последствия для изображений и текстов. Действительно, четыре-пять неправильно принятых бита информации все же позволяют идентифицировать переданное изображение, в чем мы уже успели убедиться. Что же касается текста, то такие ошибки вполне могут привести к четырем-пяти неправильно принятым буквам и совсем не факт, что исходное сообщение удастся правильно прочитать.

Перейдем к решению поставленной задачи, причем для ее упрощения возьмем в качестве примера совсем короткое слово: o l g a.

Как и в случае с изображением, непосредственная мыслепередача текста, скорее всего, не даст требуемого результата, поэтому преобразуем заданное слово в несколько последовательностей с помощью кода ASCII. При этом, чтобы не выполнять ненужную работу по передаче и приему буквенных символов, уберем из соответствующих кодов по три первых одинаковых бита – это будут 011. Тогда получим следующие новые, уже пятиэлементные коды: o – 01111, g – 00111, l – 01100, a – 00001.

Таким образом, для передачи всего слова потребуется двадцать нулей и единиц, что примерно равно сложности матрицы круг. Далее, объединяя буквы по две – o,l g,a, … , составим 10 кодовых групп, которые оформим в виде таблицы:

Таблица 10

Двоичные последовательности для передачи индуктором

Эта таблица позволяет реализовать: однократный прием – строки 1,2 или любая другая пара; трехкратное накопление – строки 1-6 и, наконец, пятикратное накопление – строки 1-10. Процесс передачи и приема здесь ничем не отличаются от того, который мы рассмотрели выше. После приема перципиентом двоичных последовательностей, получим:

Таблица 11

Принятые перципиентом двоичные последовательности

Теперь разобьем эту таблицу на четыре части – в соответствии с количеством букв в слове (o, l, g, a). Иначе говоря, в первую часть перенесем все пять кодов, обозначенных в таблице буквой o, во вторую часть – пять кодов, обозначенных буквой l и так далее, до a. После этого, в каждой из четырех частей последовательно реализуем метод накопления – сначала трехкратный, а затем пятикратный. Но, конечно же, интересен также результат и без накопления – строки 1,2 таблицы 11.

Итак, применяя к последовательностям первых двух строк таблицы коды ASCII, в которых, как мы помним, убраны три первых бита – 011, выполним дешифрацию и получим следующий набор букв: n l g p. Правильно принятыми оказались лишь две из них – l и g. Что это за слово, определить совершенно невозможно. Продолжим обработку принятых данных, реализуя трехкратное накопление, взяв для этого строки 1-6 таблицы 11. В результате дешифрации получим новый набор буквенных символов: o h g a. Здесь правильно идентифицированными оказались уже три буквы из четырех – o, g и a. Однако, если заранее не знать, о каком слове идет речь, то и на этом этапе определить, что же было передано, довольно затруднительно. Не остается ничего другого, как продолжить процесс приема, используя пятикратное накопление – все строки таблицы 11, что, в конце концов, приводит нас к идеальному результату – o l g a.

Рассмотренным примером мы еще раз подтвердили эффективность мысленного способа передачи информации, распространив его на текстовые сообщения.

Выводы. Приведенные выше результаты экспериментов показали не только возможность мысленной передачи сообщений, но и продемонстрировали простой способ ее реального воплощения. Учитывая низкую пропускную способность канала связи индуктор – перципиент, предлагается любую информацию, будь то изображение, текст или звук, предварительно преобразовать в бинарные последовательности заданной длины, которые затем передавать, используя известные методы защиты от ошибок, например, метод накопления. При этом следует принять во внимание и психологические особенности участников передачи, в частности, в качестве нулей и единиц целесообразно выбрать наиболее информативные и существенно отличающиеся друг от друга изображения. При надлежащем подборе пары индуктор-перципиент и использовании метод накопления, можно добиться вероятности правильного приема сообщения сколь угодно близкой к единице.